Giới thiệu
Trong phần trước mình đã hướng dẫn dùng các đường thẳng và đường tròn để vẽ biểu đồ RadaChart. Như đã hứa, trong phần này mình sẽ hướng dẫn vẽ chú chim trong truyền thuyết của Swift.

Phân tích
- Để vẽ được hình như trên chúng ta 2 bước:
- Vẽ đường cong bao quanh,
- Tô màu cho đường bao.
Vẽ đường cong:
Để vẻ được đường những đường cong trong đồ hoạ, chúng ta cần hiểu được về đường cong Bezier.
" Đường cong Bézier là một đường cong tham số thường được sử dụng trong đồ họa máy tính và một số lĩnh vực khác. Dạng tổng quát hóa của đường cong Bézier trong không gian nhiều chiều được gọi là mặt phẳng Bézier, trong đó tam giác Bézier là một trường hợp đặc biệt. Đường cong Bézier được công bố lần đầu vào năm 1962 bởi một kỹ sư người Pháp Pierre Bézier, người sử dụng nó để thiết kế thân ôtô. Nhưng việc nghiên cứu những đường cong này thực tế đã bắt đầu từ năm 1959 bởi nhà toán học Paul de Casteljau, ông sử dụng giải thuật De Casteljau để đánh giá các đường cong đó. Về mặt ứng dụng, đường cong Bézier thường được sử dụng trong đồ họa vector để mô hình hóa các đường cong mượt (smooth curves) và những đường cong đó có thể được phóng to hoặc thu nhỏ theo một tỉ lệ không giới hạn. "Đường dẫn" (path), một khái niệm được sử dụng trong các chương trình xử lý ảnh, được tạo ra bằng cách liên kết các đường cong Bézier với nhau. Đường cong Bézier còn thường được sử dụng như là một công cụ để điều khiển sự chuyển động (animation)." -Wikipedia-
Trong đường cong bezier chúng ta cần quan tâm về điểm bắt đầu P1, và điểm kế thúc Pn. Ngoài ra còn có các điểm control point nằm ngoài đường cong. Bậc của đường cong Bezier phụ thuộc vào số lượng điểm control Point.
Đường thẳng tuyến tính (Linear)
Đường cong bậc 1 với P1 và P2 và ko có điểm control point. Đây là đường thẳng tuyến tính đi chạy từ P1 đến P2. 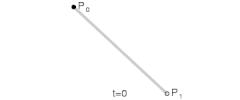
- Phương trình.
![]()
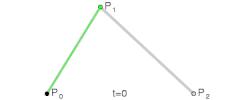
Đường cong bậc 2 (Quadric)
Đường cong Quadric là đường cong bậc 2 gồm điểm bắt đầu P0, điểm kết thúc P2 và 1 điểm control point P1.
Phương trình:
![]()
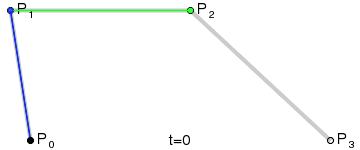
Đường bậc 3 (Cubic)
Đường cong Quadric là đường cong bậc 2 gồm điểm bắt đầu P0, điểm kết thúc P3 và 2 điểm control point P1, P2. Đường con bậc 3 được kết hợp từ 2 đường cong bậc 2 với nhau:
Phương trình:
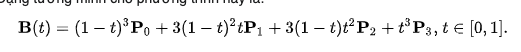
Bắt đầu vẽ đường bao
Trên đây là 1 ít lí thuyết toán học khô khan, tiếp theo chúng ta áp dụng chúng vào Swift. Rất may mắn, iOs đã hỗ trợ chúng ta "tận răng" để việc này trở nên dễ dàng hơn.
- Các hàm vẽ đường cong với UIBezierPath():
- func addQuadCurve(to endPoint: CGPoint, controlPoint: CGPoint)
- func addCurve(to endPoint: CGPoint, controlPoint1: CGPoint, controlPoint2: CGPoint)
Tương tự như vẽ đường thẳng, iOs hỗ trợ chúng ta dùng hàm addQuandCurve , và addCurve để vẽ đường cong bậc 2 và bậc 3.
override func draw(_ rect: CGRect) {
super.draw(rect)
let path = UIBezierPath()
path.move(to: CGPoint(x: 0, y: 0))
path.addQuadCurve(to: CGPoint(x: 30, y: 120), controlPoint: CGPoint(x: 100, y: 100))
path.stroke()
}
Kết quả:

Tuy nhiên, yêu cầu của chúng ta là vẽ được đường thẳng cho trước nhưng lại chưa thể xác định được control point của đường cong. Vì vậy, chúng ta cần phải tìm ra điểm control point đó từ các điểm cho trước nằm trên đường cong. May mắn là mình đã tìm được 1 cách để xác định 2 control point từ 4 điểm cho trước của đường cong bậc 2.
func controlPoint(x1:CGPoint ,x2: CGPoint, x3: CGPoint, x4: CGPoint) -> (CGPoint, CGPoint) {
let f1: CGFloat = 0.296296296296296296296; // (1-1/3)^3
let f2: CGFloat = 0.037037037037037037037; // (1-2/3)^3
let f3: CGFloat = 0.296296296296296296296; // (2/3)^3
let b1 = x2.y - x1.y * f1 - x4.y / 27.0
let b2 = x3.y - x1.y * f2 - f3 * x4.y
let c1 = (-2 * b1 + b2) / (-0.66666666)
let c2 = (b2 - 0.2222222 * c1) / 0.444444444
return(CGPoint(x: x2.x, y: c1), CGPoint(x: x3.x, y: c2))
}
- Với x2, và x3 là các điểm có vị trí 1/3 và 2/3 của đường cong.
Thực hành:
Đến đây, chúng ta đã hiểu rõ cách vẽ cách đường cong theo ý muốn. Tiếp theo chúng ta sẽ bắt đầu vẽ "chú chim".
- Ta thấy "chú chim" của chúng ta được chia thành 10 đường cong bậc 2 như sau:
![]()
Để vẽ được từng đường cong này, chúng ta cần tìm được toạ độ của các đường cong, rất may chúng ta có thể tìm được toạ độ của các điểm trên ảnh nhờ tool online này:
Trên đây mình đã tìm được toạ độ của 10 đường cong trên:
let line1 = QuadraticCurvePoint(x1: CGPoint(x: 0, y: 34.8),
x2: CGPoint(x: 14.1, y: 48.2),
x3: CGPoint(x: 31.1, y: 53.6),
x4: CGPoint(x: 44.9, y: 50.5))
let line2 = QuadraticCurvePoint(x1: CGPoint(x: 44.9, y: 50.5),
x2: CGPoint(x: 50.1, y: 48.2),
x3: CGPoint(x: 56.1, y: 49.6),
x4: CGPoint(x: 59.8, y: 54.5))
let line3 = QuadraticCurvePoint(x1: CGPoint(x: 59.8, y: 54.2),
x2: CGPoint(x: 59.3, y: 46.0),
x3: CGPoint(x: 57.6, y: 41.5),
x4: CGPoint(x: 55.3, y: 38.5))
let line4 = QuadraticCurvePoint(x1: CGPoint(x: 55.3, y: 38.5),
x2: CGPoint(x: 53.6, y: 18.5),
x3: CGPoint(x: 47.2, y: 8.3),
x4: CGPoint(x: 37.2, y: 0))
let line5 = QuadraticCurvePoint(x1: CGPoint(x: 37.2, y: 0),
x2: CGPoint(x: 40.6, y: 5.7),
x3: CGPoint(x: 44.2, y: 16.3),
x4: CGPoint(x: 42.7, y: 28.6))
let line6 = QuadraticCurvePoint(x1: CGPoint(x: 42.7, y: 28.6),
x2: CGPoint(x: 34.1, y: 22.9),
x3: CGPoint(x: 25.1, y: 15.7),
x4: CGPoint(x: 13.1, y: 4.8))
let line7 = QuadraticCurvePoint(x1: CGPoint(x: 13.1, y: 4.8),
x2: CGPoint(x: 18.2, y: 12.3),
x3: CGPoint(x: 24.7, y: 20.3),
x4: CGPoint(x: 30.5, y: 26.8))
let line8 = QuadraticCurvePoint(x1: CGPoint(x: 30.5, y: 26.8),
x2: CGPoint(x: 22.8, y: 21.6),
x3: CGPoint(x: 15.3, y: 16.0),
x4: CGPoint(x: 5.9, y: 8.3))
let line9 = QuadraticCurvePoint(x1: CGPoint(x: 5.9, y: 8.3),
x2: CGPoint(x: 15.2, y: 20.2),
x3: CGPoint(x: 24.6, y: 30.2),
x4: CGPoint(x: 34.3, y: 38.8))
let line10 = QuadraticCurvePoint(x1: CGPoint(x: 34.3, y: 38.8),
x2: CGPoint(x: 23.8, y: 42.3),
x3: CGPoint(x: 11.5, y: 40.5),
x4: CGPoint(x: 0, y: 34.8))
let lines = [line1, line2, line3, line4, line5, line6, line7, line8, line9, line10]
Và tiếp theo công việc của chúng ta là nối 10 đường cong này lại như sau:
let path = UIBezierPath()
for (index, line) in lines.enumerated() {
if index == 0 {
path.move(to: line.x1)
}
let (control1, control2) = controlPoint(x1: line.x1, x2: line.x2, x3: line.x3, x4: line.x4)
path.addCurve(to: line.x4, controlPoint1: control1, controlPoint2: control2)
}
Kết quả:

- Tuyệt vời, chúng ta đã vẽ được đương bao bên ngoài của chú chim. Tiếp tục chúng ta cần dùng Gradient để tô màu cho Path đó.
Tô màu:
- Tạo Gradient layer
private let gradientLayer: CAGradientLayer = {
let gradientLayer = CAGradientLayer()
gradientLayer.startPoint = CGPoint(x: 0.1, y: 0.1)
gradientLayer.endPoint = CGPoint(x: 0.4, y: 0.4)
return gradientLayer
}()
- Tạo một mặt nạ mask với path là đường cong để đè lên backgound gradient vừa mới tạo:
gradientLayer.frame = bounds
gradientLayer.colors = [UIColor.yellow.cgColor, UIColor.red.cgColor]
let mask = CAShapeLayer()
mask.strokeColor = UIColor.white.cgColor
mask.path = path.cgPath
gradientLayer.mask = mask
- và kết quả:

Kết luận
- Vậy là trong series này mình đã giới thiệu khá đầy đủ các kiến thức cơ bản về vẽ hình đồ hoạ trong lập trình iOs, hi vọng nó sẽ giúp ích cho các bạn để có thể cày được những requirement "khoai" nhất.







