Phân cụm đồ thị là một lĩnh vực trong phân tích cụm nhằm tìm kiếm các nhóm đỉnh có liên quan trong một đồ thị. Phân cụm đồ thị cho kết quả trong mỗi cụm các đỉnh có nhiều cạnh kết nối gần, trong khi giữa các cụm thì chỉ có vài cạnh kết nối. Thuật toán Spectral Clustering sử dụng thông tin từ các giá trị riêng (phổ) của các ma trận đặc biệt được xây dựng từ đồ thị hoặc tập dữ liệu, nên nó có tên là spectral. Thuật toán xây dựng một đồ thị tương tự, chiếu dữ liệu lên không gian chiều thấp hơn và phân cụm dữ liệu. Spectral Clustering có ứng dụng trong nhiều lĩnh vực bao gồm: phân đoạn hình ảnh, khai thác dữ liệu giáo dục, phân giải thực thể, tách giọng nói, phân cụm quang phổ của chuỗi protein, phân đoạn hình ảnh văn bản.

1.Bài toán phân cụm

1.1 Học máy (Machine learning)

        Học máy hay còn gọi với cái tên Tiếng Anh là Machine Learning . Có 2 định nghĩa về Machine Learning được cung cấp. Theo Arthur Samuel mô tả: “Lĩnh vực nghiên cứu mang lại cho máy tính khả năng học hỏi mà không cần được lập trình rõ ràng.” Đây là một định nghĩa cũ, không chính thức.Tom Mitchell đưa ra một định nghĩa hiện đại và rõ ràng hơn:
“Một chương trình máy tính được cho là học hỏi từ kinh nghiệm E đối với một số loại nhiệm vụ T và thước đo hiệu suất P, nếu hiệu suất của nó ở các nhiệm vụ trong T, được đo bằng P, cải thiện theo kinh nghiệm E.”
Ví dụ: chơi cờ caro.
E = kinh nghiệm chơi nhiều ván cờ caro
T = nhiệm vụ chơi cờ caro.
P = xác suất chương trình sẽ thắng trong trò chơi tiếp theo.
    Theo phân nhóm dựa theo phương thức học, Machine learning thường được chia thành 4 loại:

• Học có giám sát (Supervised learning): thuật toán dự đoán đầu ra (outcome) của một dữ liệu mới (new input) dựa trên các cặp (input, outcome) đã biết từ trước.
• Học không giám sát (Unsupervised learning): chỉ có dữ liệu vào X mà không biết label Y tương ứng. Chúng ta không biết được đầu ra hay nhãn mà chỉ có dữ liệu đầu vào. Thuật toán unsupervised learning sẽ dựa vào cấu trúc của dữ liệu để thực hiện một công việc nào đó.
• Học bán giám sát (Semi-Supervised Learning): chúng ta có một lượng lớn dữ liệu X nhưng chỉ một phần trong chúng được gán nhãn.
• Học củng cố (Reinforcement Learning): các bài toán giúp cho một hệ thống tự động xác định hành vi dựa trên hoàn cảnh để đạt được lợi ích cao nhất (maximizing the performance).

1.2 Phân cụm (Clustering)

        Phân cụm (Clustering) thuộc loại học không giám sát (Unsupervised learning) là một dữ liệu là bài toán gom nhóm các đối tượng dữ liệu vào thánh từng cụm (cluster) sao cho các đối tượng trong cùng một cụm có sự tương đồng theo một tiêu chí nào đó. Ví dụ: phân nhóm khách hàng dựa trên hành vi mua hàng. Điều này cũng giống như việc ta đưa cho một đứa trẻ rất nhiều mảnh ghép với các hình thù và màu sắc khác nhau, ví dụ tam giác, vuông, tròn với màu xanh và đỏ, sau đó yêu cầu trẻ phân chúng thành từng nhóm. Mặc dù không cho trẻ biết mảnh nào tương ứng với hình nào hoặc màu nào, nhiều khả năng chúng vẫn có thể phân loại các mảnh ghép theo màu hoặc hình dạng. Đặc điểm của phân cụm: -Số cụm dữ liệu không được biết trước -Có nhiều các tiếp cận, mối cách lại có vài kỹ thuật -Các kỹ thuật khác nhau thường mang lại kết quả khác nhau.

2.Thuật toán Spectral Clustering

2.1 Mã giả

    1. Tính ma trận kề

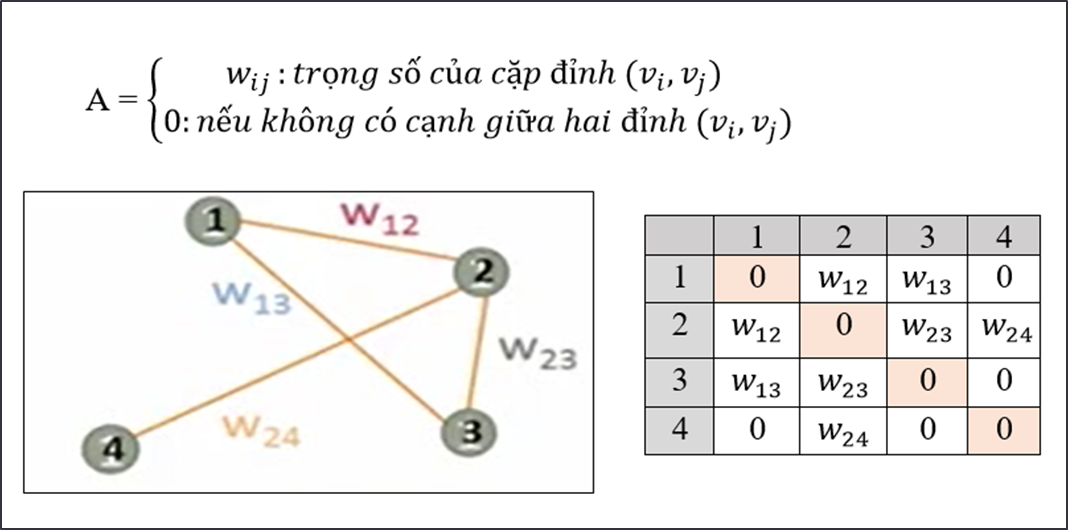
    Cho đồ thị G = (V, E) với V là tập gồm các đỉnh và E là tập gồm các cạnh. Mỗi cạnh thuộc E sẽ gồm 2 đỉnh trong tập V - một cặp đỉnh (𝑣_𝑖, 𝑣_𝑗), với trọng số cạnh là 𝑤_𝑖𝑗.

    2. Tính ma trận Laplacian

    Ma trận laplacian: L = D-A với D là ma trận bậc. Ma trận bậc D được tính từ ma trận kề A, có số chiều giống với ma trận A. Mỗi phần tử trên đường chéo chính của ma trận bậc D là tổng của của các phần tử trên một hàng của ma trận A tương ứng. Các phần tử khác ngoài đường chéo chính đều bằng 0.

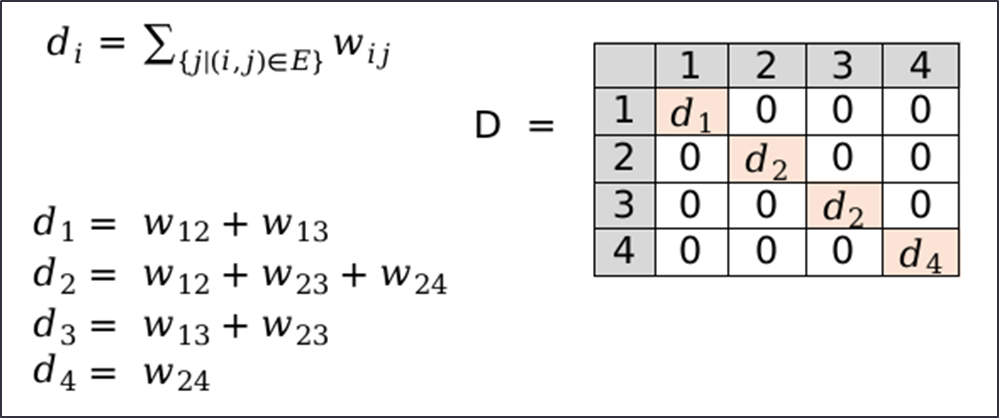
    Ma trận laplacian:

    3. Tính k vector riêng đầu tiên của ma trận Laplacian
Cho một ma trận A, ta có 𝜆 là một giá trị riêng và 𝜈 là vector riêng của A nếu:
A𝝂 = 𝝀𝝂
Cho một đồ thị G có n nút, ma trận kề của nó sẽ có n giá trị riêng {𝜇_1, 𝜇_2, 𝜇_3…, 𝜇_𝑛} với 𝜇_1 ≥ 𝜇_2 ≥ 𝜇_3 ≥…≥ 𝜇_𝑛 và n vector riêng {𝑥_1, 𝑥_2, 𝑥_3,…, 𝑥_𝑛}

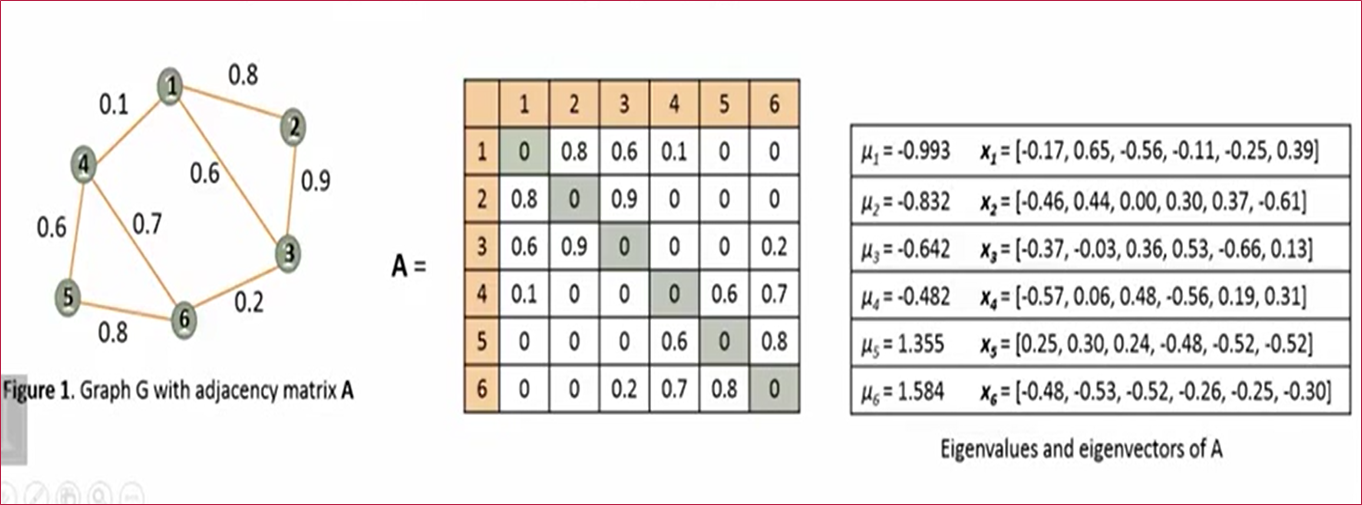
    Ở đây ta sẽ đi tính véc tơ riêng và giá trị riêng cho ma trận Laplacian, sau đó lấy ra k vector đầu tiên. Có thể nói việc tính ma trận Laplacian và tính k giá trị riêng và vector riêng của ma trận này là trái tim của thuật toán Spectral Clustering. Các giá trị riêng cho biết các thuộc tính toàn cục không rõ ràng của đồ thị từ cấu trúc cạnh. Xét đồ thị Laplacian của G, 𝐿_𝐺 có tập giá trị riêng {𝜆_1, 𝜆_2, 𝜆_3,…, 𝜆_𝑛} và tập vector {𝑥_1,𝑥_2,𝑥_3,…,𝑥_𝑛}:

• Nếu 0 là giá trị riêng của L (𝜆_1=𝜆_2=…=𝜆_𝑘=0) với k vector riêng thì đồ thị G có k kết nối thành phần
• Nếu đồ thị đã được kết nối, 𝜆_2 > 0 và 𝜆_2 là kết nối đại số của G, 𝜆_2 càng lớn thì G càng có nhiều kết nối.

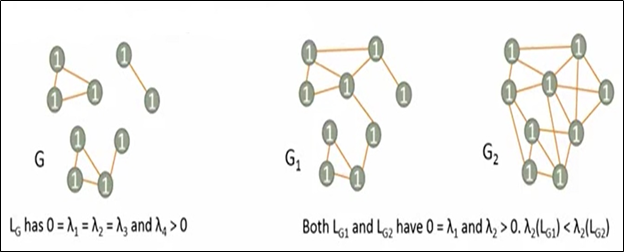
    Dễ thấy rằng L_G có λ_1 = λ_2 = λ_3 = 0 và λ_4 > 0 nên G có 3 đường kết nối. L_G1 và L_G2 có λ_1 = 0 nên 2 đồ thị G1 và G2 có một đường kết nối.
Lại có λ_2 (L_G1 ) < λ_2 (L_G2) nên G2 có nhiều đường kết nối hơn.

    4. Sử dụng K-means để phân cụm
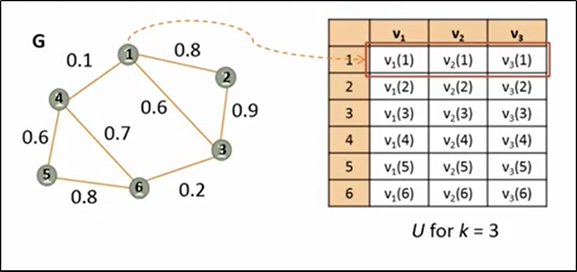
Sắp xếp thành ma trận U với k véc tơ riêng đầu tiên của ma trận L và các đỉnh của đồ thị G (ký hiệu v trong hình là véc tơ riêng, không phải đỉnh). Sau đó áp dụng phân cụm đối với ma trận U sử dụng thuật toán K-mean để phân các đỉnh của G (hàng của U).

    Thuật toán K-mean
Input: K (số lượng các cụm), Training set {𝑥^((1)), 𝑥^((2)),…,𝑥^((𝑚)) } 𝑥^((𝑖))∈ℝ^𝑛
Output:  Các center 𝜇_𝐾 và label cho từng điểm dữ liệu 𝑥^((𝑖)).

1. Chọn K điểm bất kỳ làm các center ban đầu.
2. Phân mỗi điểm dữ liệu vào cụm có center gần nó nhất.
3. Nếu việc gán dữ liệu vào từng cụm ở bước 2 không thay đổi so với vòng lặp trước nó thì ta dừng thuật toán.
4. Cập nhật center cho từng cụm bằng cách lấy trung bình cộng của tất các các điểm dữ liệu đã được gán vào cluster đó sau bước 2.
5. Quay lại bước 2.

2.2 Ưu và nhược điểm của thuật toán

    
     Spectral Clustering giúp chúng ta khắc phục hai vấn đề chính trong phân cụm: một là hình dạng của cụm và vấn đề khác là xác định tâm của cụm. Thuật toán K-mean thường giả định rằng các cụm là hình cầu hoặc tròn, dùng nhiều lần lặp để xác định tâm cụm và phân các điểm. Trong spectral clustering, các cụm không tuân theo một hình dạng hoặc khuôn mẫu cố định. Các điểm ở xa nhau nhưng được kết nối thuộc cùng một cụm và các điểm ít xa nhau hơn có thể thuộc các cụm khác nhau nếu chúng không được kết nối. Điều này có nghĩa là thuật toán có thể hiệu quả đối với dữ liệu có hình dạng và kích thước khác nhau.
     Khi so sánh với các thuật toán khác, nó nhanh về mặt tính toán đối với các tập dữ liệu thưa thớt vài nghìn điểm dữ liệu mặc dù có thể tốn kém để tính toán cho các tập dữ liệu lớn vì các giá trị riêng và vector cần được tính toán và sau đó mới thực hiện phân cụm.

3. Cài đặt thuật toán

• Code python cài đặt thuật toán từng bước theo mã giả ở trên, mình đã trình bày chi tiết trên Google Colab: https://drive.google.com/file/d/1tua2gx4J7k8jhVCkm8-7gjFVx-j0wqrc/view?usp=sharing
• Khi đã nắm chắc, các bạn có thể sử dụng hàm có sẵn của thư viện Sklearn cho thuật toán: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.SpectralClustering.html

4. Tài liệu tham khảo

• https://www.analyticsvidhya.com/blog/2021/05/what-why-and-how-of-spectral-clustering/
• https://www.kdnuggets.com/2020/05/getting-started-spectral-clustering.html
• https://machinelearningcoban.com/2017/01/01/kmeans/
• https://machinelearningcoban.com/2016/12/26/introduce/