I. Khái niệm về đồ thị

1. Sơ lược về Lý thuyết đồ thị

    Trong Toán học và Tin học, Lý thuyết đồ thị tập trung nghiên cứu về một đối tượng cơ bản là đồ thị - một đối tượng có tính ứng dụng rất cao trong thực tế. Mô hình đồ thị xuất hiện xung quanh ta, trong nhiều lĩnh vực của cuộc sống, như giao thông, cấu trúc website,...

    Mô hình bài toán 7 cây cầu ở Königsberg

    Người đặt nền móng cho sự phát triển của Lý thuyết đồ thị là Leonhard Euler - nhà toán học người Thụy Sĩ. Thông qua việc đưa ra lời giải cho bài toán $7$ cây cầu ở Königsberg vào năm $1736$, ông đã chính thức khai sinh lý thuyết đồ thị.

    Một cách trừu tượng hóa, đồ thị là một tập các đối tượng được gọi là các đỉnh (hoặc nút) được nối với nhau bằng các cạnh (hoặc cung) và được biểu diễn theo nhiều cách khác nhau trong Toán học và Tin học.

2. Định nghĩa và phân loại đồ thị

    Một đồ thị là một cấu trúc rời rạc gồm tập hợp các đỉnh và các cạnh nối giữa các đỉnh đó. Có thể mô tả đồ thị theo cách hình thức như sau:

    $$G=(V,E)$$

    tức là đồ thị $G$ có tập các đỉnh là $V$, tập các cạnh là $E$. Có thể hiểu $E$ là tập hợp các cặp $(u, v)$ với $u$ và $v$ là hai đỉnh thuộc $V$.

    Có thể phân loại đồ thị $G$ theo tính chất của tập cạnh như sau:

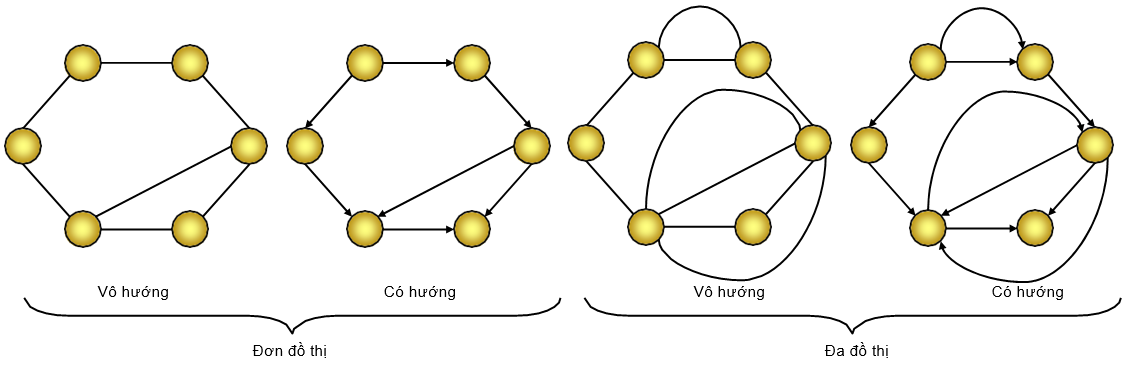
• $G$ được gọi là đơn đồ thị nếu như giữa hai đỉnh $(u, v)$ của $V$ có nhiều nhất một cạnh trong $E$ nối từ $u$ tới $v$.
• $G$ được gọi là đa đồ thị nếu như giữa hai đỉnh $(u, v)$ của $V$ có thể có nhiều hơn $1$ cạnh nối trong $E$ nối từ $u$ tới $v$. Hiển nhiên đơn đồ thị cũng là đa đồ thị.
• $G$ được gọi là đồ thị vô hướng (undirected graph) nếu như các cạnh trong $E$ là không định hướng, tức là cạnh $(u, v)$ là cạnh hai chiều.
• $G$ được gọi là đồ thị có hướng (directed graph) nếu như các cạnh trong $E$ là có định hướng, tức là có thể tồn tại cạnh nối từ u tới v nhưng chưa chắc đã tồn tại cạnh nối từ v tới u. Trên đồ thị có hướng, các cạnh sẽ được gọi là các cung. Đồ thị vô hướng cũng có thể coi là đồ thị có hướng, nếu như ta coi cạnh $(u, v)$ bất kỳ tương ứng với hai cung $(u\rightarrow v)$ và $(v \rightarrow u)$.

II. Các khái niệm trên đồ thị

1. Cạnh liên thuộc, đỉnh kề, bậc và khuyên

    Đối với đồ thị vô hướng $G=(V, E),$ xét cạnh $e = (u, v) \in E$. Ta nói rằng hai đỉnh $u$ và $v$ kề nhau (adjacent), và cạnh $e$ này liên thuộc (incident) với hai đỉnh $u$ và $v$.

    Với một đinh u thuộc đồ thị, định nghĩa bậc (degree), ký hiệu $deg(u)$ là số cạnh liên thuộc với $u$. Trên đơn đồ thị, số cạnh liên thuộc với $u$ cũng chính là số đỉnh kề với $u$.

Định lý 1

    Giả sử $G=(V, E)$ là đồ thị vô hướng với $M$ cạnh khi đó tổng tất cả các bậc đỉnh trong $V$ sẽ bằng $2M$.

    $$\sum_{v \in V} deg(v)=2M$$

    Chứng minh: Khi lấy tổng tất cả các bậc đỉnh, tức là mỗi cạnh $e=(u, v)$ bất kỳ sẽ được tính một lần trong $deg(u)$ và một lần trong $deg(v)$. Từ đó suy ra điều phải chứng minh.

    Hệ quả: Trên đồ thị vô hướng, số đỉnh bậc lẻ là một số chẵn.

    Đối với đồ thị có hướng $G=(V, E)$, xét một cung $e=(u \rightarrow v) \in E$. Khi đó ta nói đỉnh u nối tới đỉnh v và đỉnh v nối từ đỉnh u. Đỉnh $u$ được gọi là đỉnh đầu, đỉnh $v$ được gọi là đỉnh cuối của cung $e$.

    Với mỗi đỉnh u trong đồ thị có hướng, định nghĩa: Bán bậc ra (out-degree) của đỉnh $u$, kí hiệu $deg^+(u)$ là số cung đi ra khỏi nó; Bán bậc vào (in-degree) của đỉnh $u$, kí hiệu $deg^-(u)$ là số cung đi vào nó.

Định lý 2

    Giả sử $G=(V, E)$ là đồ thị có hướng với M cung, khi đó tổng tất cả các bán bậc ra bằng tổng tất cả các bán bậc vào và bằng $M$:

    $$\sum_{v \in V} deg^+(v)=\sum_{v \in V} deg^-(v)=M$$

    Chứng minh: Khi lấy tổng tất cả các bán bậc ra hoặc bán bậc vào, mỗi cung $(u\rightarrow v)$ bất kỳ sẽ được tính đúng một lần trong $deg^+(u)$ và cũng được tính đúng một lần trong $deg^-(v)$. Từ đó suy ra điều phải chứng minh.

    Ngoài ra, trên đồ thị có hướng hoặc vô hướng, trong một số trường hợp có thể có những cạnh nối một đỉnh với chính nó. Cạnh này được gọi là khuyên của đồ thị, và trong trường hợp này, thì các cạnh nối hai đỉnh phân biệt sẽ được gọi là các liên kết để tránh nhầm lẫn.

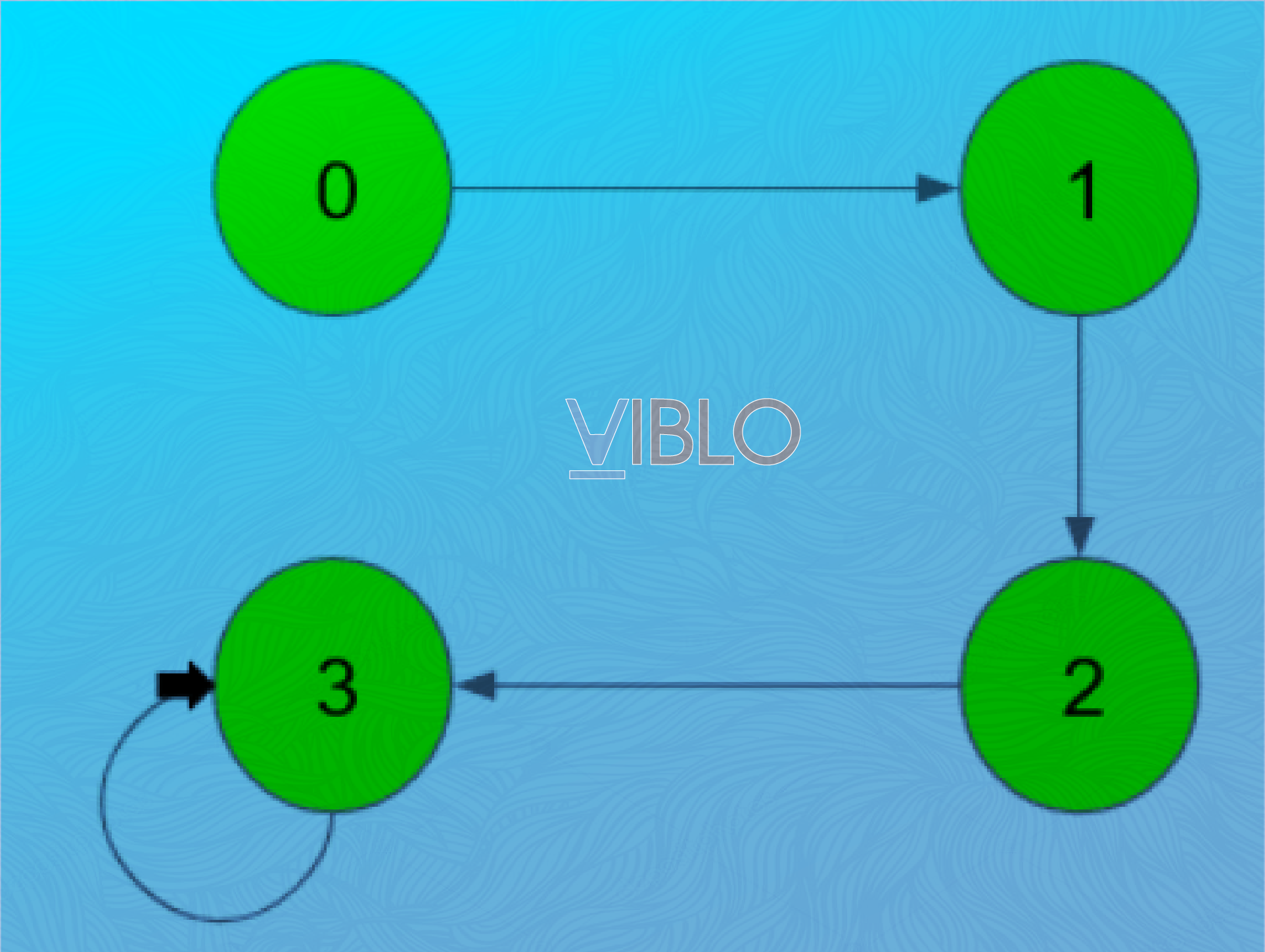
    Đồ thị có khuyên ở đỉnh 3

2. Đường đi và chu trình

    Một đường đi $P$ độ dài $k$ từ đỉnh $v_0$ tới đỉnh $v_k$ là tập đỉnh $\{v_0, v_1, v_2,..., v_k\}$ sao cho $(v_{i - 1},v_i) \in E, \forall i: 1 \le i \le k$. Khi đó ta nói đường đi này bao gồm các đỉnh $\{v_0, v_1, v_2,..., v_k\}$ và các cạnh $\{(v_0, v_1), (v_1, v_2), ..., (v_{k - 1}, v_k)\}$; và $v_0$ đến được $v_k$ thông qua đường đi $P$.

    Đường đi được gọi là đường đi đơn giản (simple path) nếu tất cả các đỉnh trên đường đi đó đều phân biệt. Đường đi được gọi là đường đi đơn nếu như không có cạnh nào trên đường đi đó đi qua hơn một lần.

    Một đường đi con (subpath) $P'$ của $P$ là một đoạn liên tục các đỉnh và cạnh dọc theo đường đi $P$.

    Đường đi $P$ gọi là chu trình (circuit) nếu như $v_0=v_k$. Chu trình $P$ gọi là chu trình đơn giản (simple circuit) nếu như $\{v_1, v_2,..., v_k\}$ đôi một khác nhau. Chu trình mà trong đó không có cạnh nào đi qua hơn một lần được gọi là chu trình đơn.

3. Tính liên thông của đồ thị

    Đối với đồ thị vô hướng $G=(V, E)$ thì $G$ được gọi là liên thông nếu như với mọi cặp đỉnh phân biệt $(u, v)$, ta đều có $u$ đến được $v$ (đồng nghĩa với $v$ cũng đến được $u$).

    Đối với đồ thị có hướng $G=(V, E)$:

• $G$ được gọi là liên thông mạnh (strongly connected) nếu với mọi cặp đỉnh phân biệt $(u, v)$, ta có $u$ đến được $v$ và $v$ đến được $u$.
• $G$ được gọi là liên thông yếu (weakly connected) nếu như đồ thị vô hướng nền của nó là liên thông (tức là hủy bỏ chiều của các cạnh trên đồ thị).
• $G$ được gọi là liên thông một phần (unilaterally connected) nếu như với mọi cặp đỉnh phân biệt $(u, v),$ có ít nhất một đỉnh đến được đỉnh còn lại.

III. Tài liệu tham khảo

• https://vi.wikipedia.org/wiki/L%C3%BD_thuy%E1%BA%BFt_%C4%91%E1%BB%93_th%E1%BB%8B
• Sách Giải thuật và Lập trình - thầy Lê Minh Hoàng.
• Tài liệu giáo khoa chuyên Tin quyển 1 - thầy Hồ Sĩ Đàm.