Ở bài viết trước, Cấu trúc dữ liệu và giải thuật: Danh sách liên kết đơn (Singly Linked List). Mình đã giới thiệu về danh sách liên kết, và 'biến thể' của cấu trúc dữ liệu này. Trong bài viết này, mình sẽ hướng dẫn cách cài đặt thuật toán cho danh sách liên kết đôi (Doubly Linked List).
Mình sẽ giới thiệu lại một chút danh sách liên kết đôi:
- Danh sách liên kết đôi (Doubly Linked List): Mỗi node trong danh sách liên kết đôi gồm có previous pointer, data và next pointer, previous pointer trỏ tới phần tử đứng trước, next pointer trỏ tới phần tử phía sau. Nếu previous pointer trỏ tới NULL thì có nghĩa node đó là node đứng đầu tiên trong danh sách liên kết đơn. Và tương tự với danh sách liên kết, next pointer trỏ tới NULL thì đó là node cuối trong danh sách liên kết đơn.
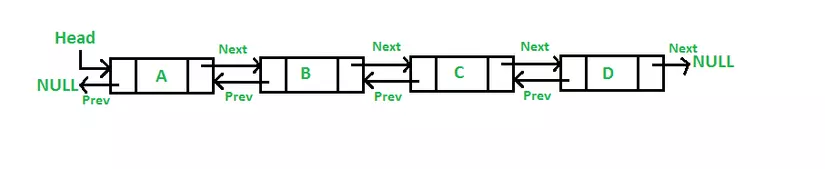
- Không giống như danh sách liên kết đơn, xóa 1 node trong list cần biết node đứng trước nó. Thì trong danh sách liên kết đôi, có thể xóa 1 node trong list mà không cần dựa vào node đứng trước nó mà chỉ cần dựa vào node đứng sau nó.
- Với mỗi node, có thêm một con trỏ previous pointer dẫn tới sẽ cần thêm bộ nhớ.
- Thêm hoặc xóa 1 node trong danh sách liên kết đôi, sẽ lâu hơn 1 chút so với danh sách liên kết đơn.
1. Setup
-
Các bạn có thể clone source code thuật toán tại đây: https://github.com/DucLS/Data-structure-algorithm/tree/main/linked-list
-
Vẫn như thường lệ, mình sẽ khởi tạo với một class Node như sau:
class Node {
constructor(value, prev, next) {
this.value = value;
this.prev = prev;
this.next = next;
}
}
- Và khởi tạo thêm một class DoublyLinkedList:
class DoublyLinkedList {
constructor() {
this.head = null;
this.length = 0;
}
}
- Khởi tạo một method, có tác dụng lấy node ở vị trí bất kỳ trong danh sách:
getNodeAtIndex(index) {
if (index < 0 || index >= this.length) {
return null;
}
if (index == 0) {
return this.head;
}
let currentNode = this.head;
for (let i = 1; i <= index; i++) {
if (currentNode) {
currentNode = currentNode.next;
}
}
return currentNode;
}
2. Doubly Linked List Insertion Cũng giống như danh sách sách liên kết đơn, đối với danh sách liên kết đôi, chèn 1 node vào trong list, cũng có 3 loại:
- Chèn vào vị trí đầu của danh sách.
- Chèn vào vị trí của cuối danh.
- Chèn vào vị trí bất kỳ của danh sách.
Chèn vào vị trí đầu của danh sách
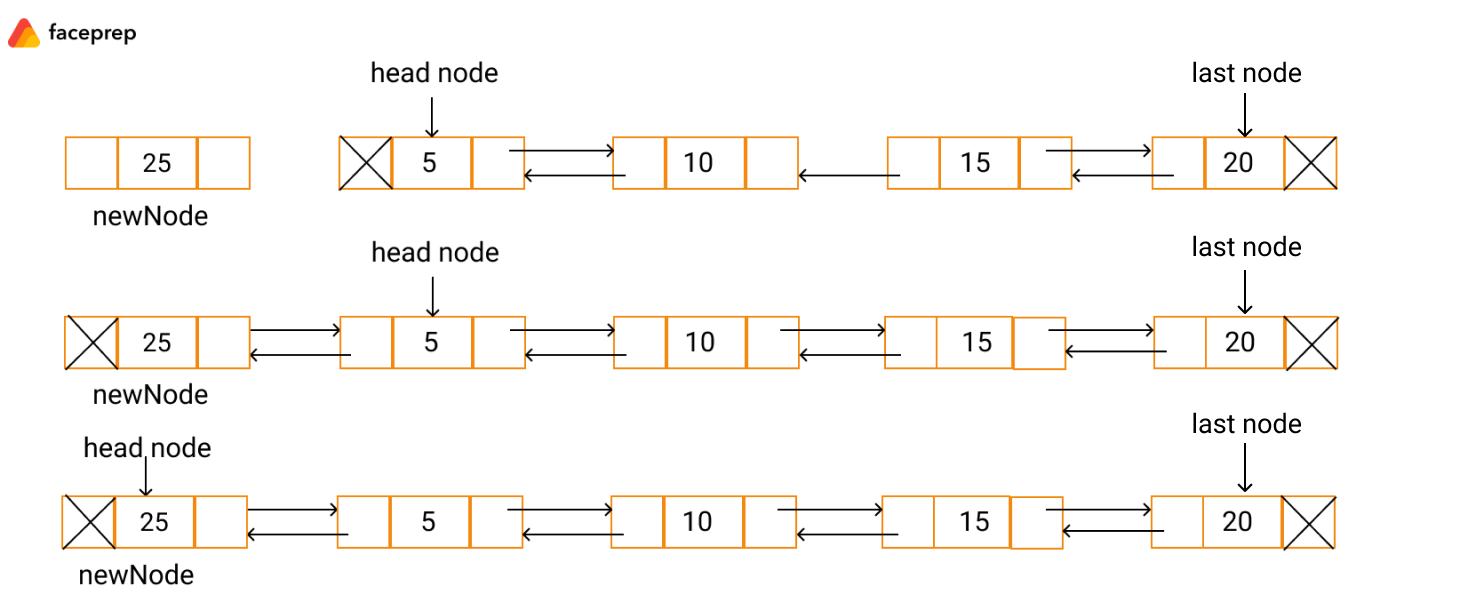
Để chèn 1 node vào vị trí đầu của danh sách, cần làm 2 bước sau:
- Tạo một node, với prev pointer trỏ tới null, và next ponter trỏ tới head node hiện tại.
- Gán prev pointer của head node hiện tại trỏ tới node vừa tạo, và update lại head node chính là node vừa tạo.
Cụ thể, thuật toán sẽ như sau:
insertAtHead(data) {
const node = new Node(data, null, this.head);
if (this.head) {
this.head.prev = node;
}
this.head = node;
this.length ++;
return;
}
Chèn vào vị trí cuối của danh sách
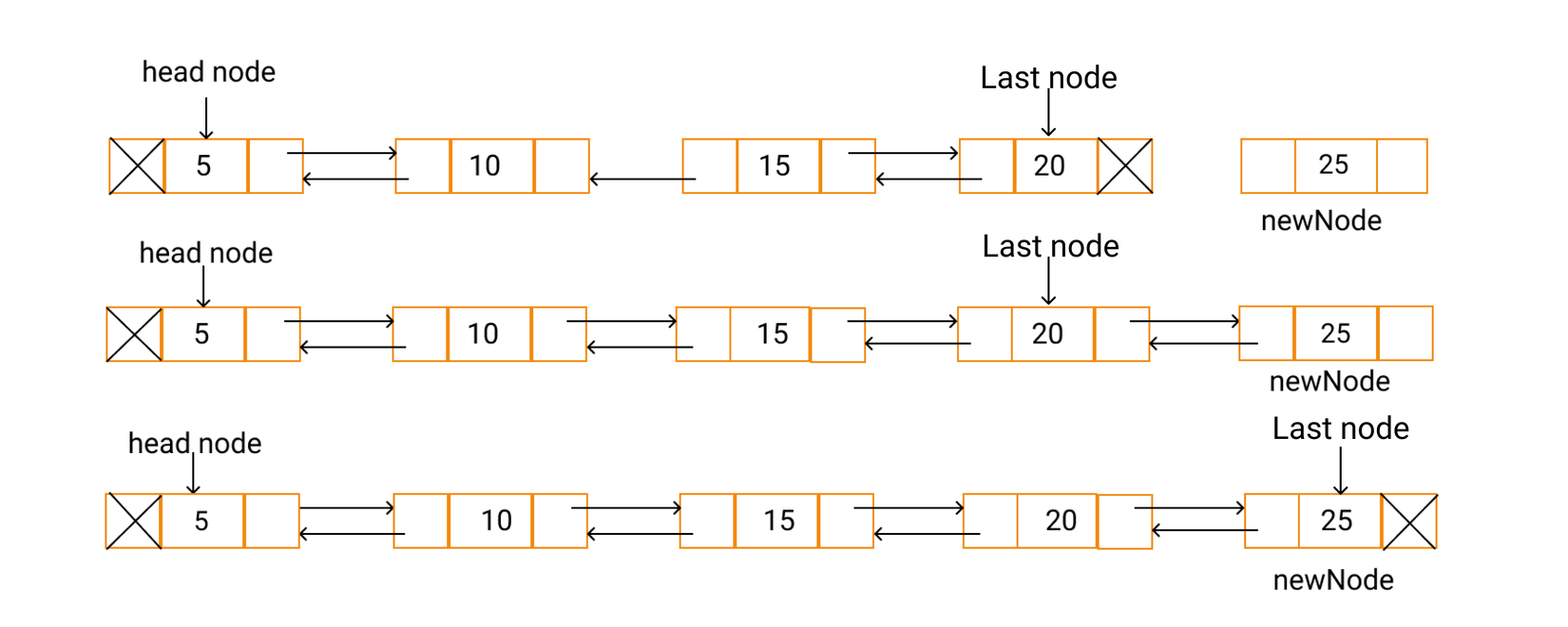
Để chèn 1 node vào vị trí cuối của danh sách, cần làm 3 bước sau:
- Lấy tail node của danh sách.
- Tạo một node mới, với prev pointer trỏ tới tail node, next pointer trỏ tới null.
- Gán next ponter của tail node hiện tại, trỏ tới node vừa tạo, và update lại tail node chính là node vừa tạo.
Cụ thể, thuật toán như sau:
insertAtTail(data) {
if (!this.head) {
return this.insertAtHead(data);
}
const prevNode = this.getNodeAtIndex(this.length - 1);
const node = new Node(data, prevNode, null);
prevNode.next = node;
this.length ++;
return;
}
Chèn vào vị trí bất kỳ trong danh sách
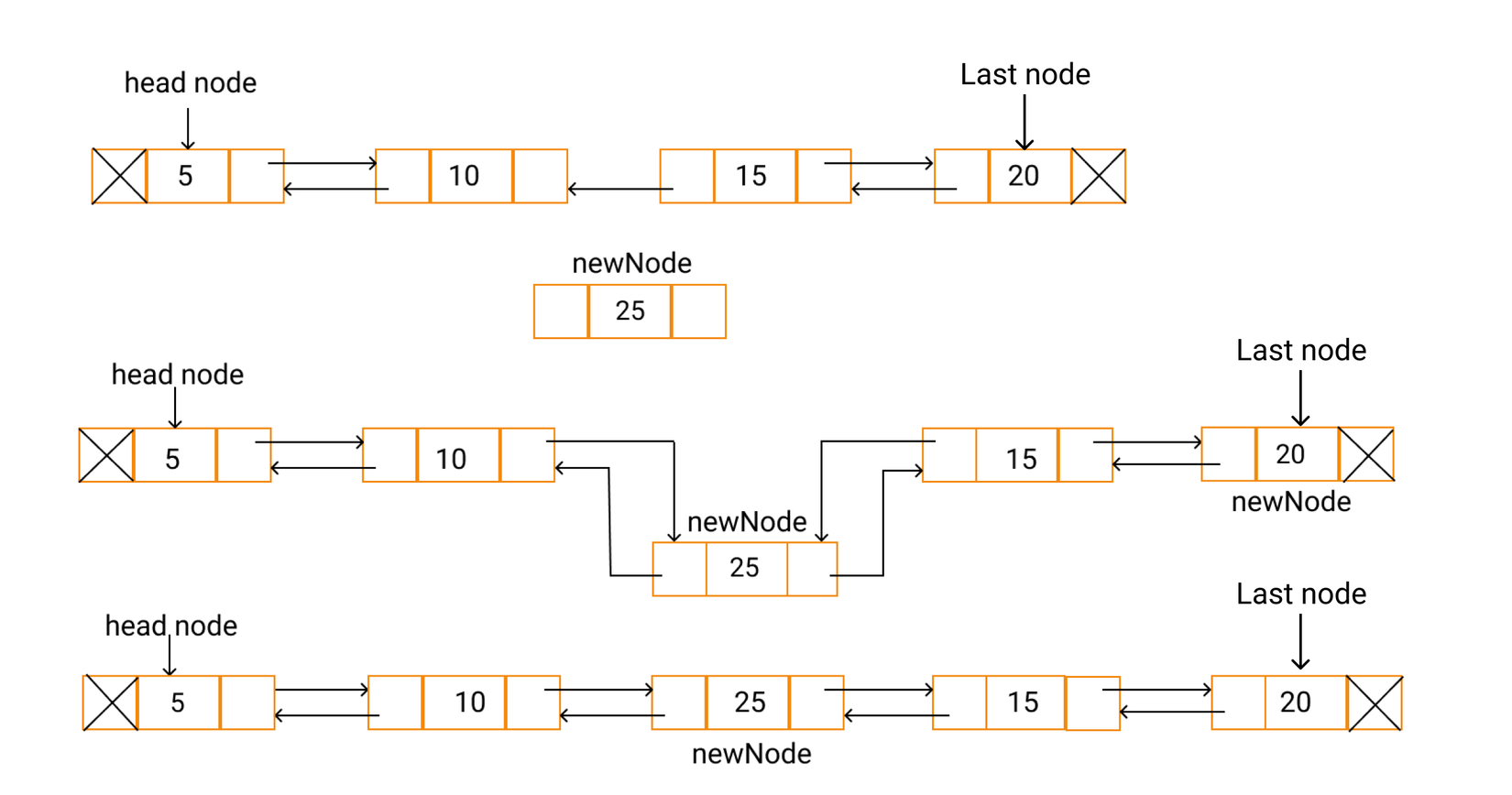
Để chèn 1 node vào vị trí bất kỳ trong danh sách, cần làm 3 bước sau:
- Lấy node ở vị trí trước vị trí cần chèn gọi là prevNode, node sau vị trí cần chèn gọi là nextNode.
- Tạo một một node mới, với prev pointer trỏ tới prevNode , next pointer trỏ tới nextNode.
- Update next pointer của prevNode và prev pointer của nextNode trỏ tới node vừa tạo.
Cụ thể, thuật toán sẽ như sau:
insertAtIndex(data, index) {
if (index === 0) {
return this.insertAtHead(data);
}
if (index === this.length) {
return this.insertAtTail(data);
}
const prevNode = this.getNodeAtIndex(index - 1);
const node = new Node(data, prevNode, prevNode.next);
prevNode.next.prev = node;
prevNode.next = node;
this.length ++;
return;
}
3. Doubly Linked List Deletion
Cũng tương tự như chèn, thì xóa 1 node trong list cũng có 3 loại:
- Xóa ở vị trí đầu của danh sách.
- Xóa ở vị trí cuối của danh sách.
- Xóa ở vị trí bất kỳ trong danh sách.
Xóa ở vị trí đầu của danh sách
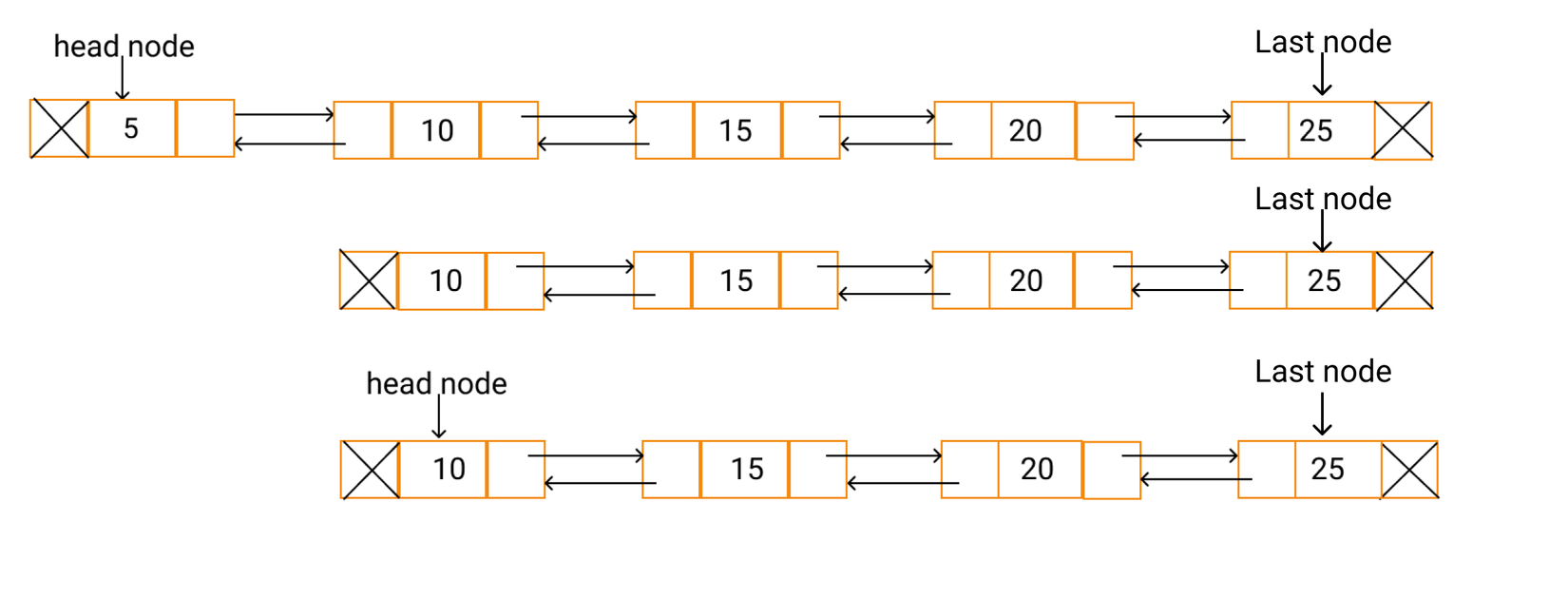
Để xóa head node, mình làm 2 bước sau:
- Lấy nextNode của head node.
- Update prev pointer của nextNode trỏ tới null, và update head node là nextNode.
Cụ thể, thuật toán sẽ như sau:
deleteAtHead() {
if (this.length === 1) {
this.head = null;
this.length = 0;
return;
}
const nextNode = this.head.next;
nextNode.prev = null;
this.head = nextNode;
this.length --;
return;
}
Xóa ở vị trí cuối của danh sách
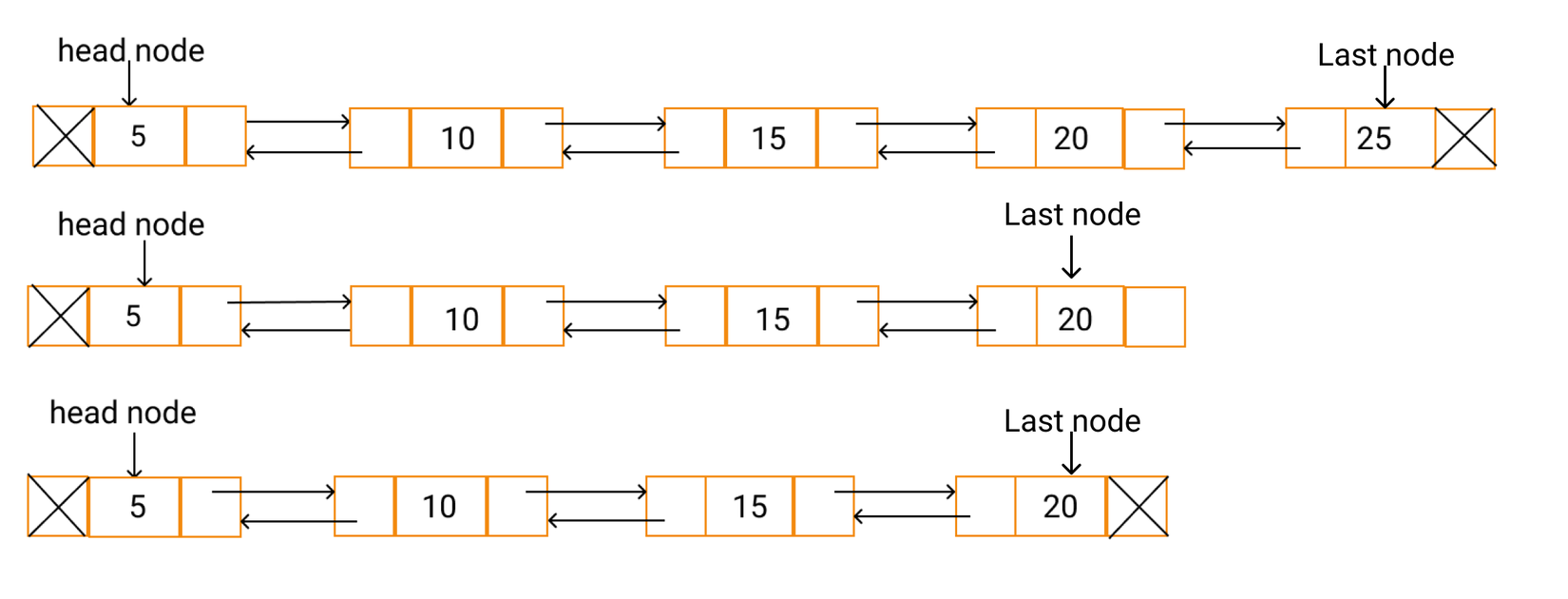
Để xóa tail node, mình làm 2 bước sau:
- Lấy node ở vị trí kế cuối, gọi là prevNode.
- Update next pointer của prevNode là NULL.
Thuật toán sẽ như sau:
deleteAtTail() {
if (this.length === 1) {
return this.deleteAtHead();
}
const prevNode = this.getNodeAtIndex(this.length - 2);
prevNode.next = null;
this.length --;
return;
}
Xóa ở vị trí bất kỳ trong danh sách

Để xóa 1 node, ở vị trí bất kỳ. Mình làm như sau:
- Lấy node ở vị trí cần xóa, node đứng trước gọi là prevNode, node đứng sau gọi là nextNode.
- Update next pointer của prevNode trỏ tới nextNode.
- Update prev ponter của nextNode trỏ tới prevNode.
Thuât toán như sau:
deleteAtIndex(index) {
if (index < 0 || index >= this.length) {
return null;
}
if (index === 0) {
return this.deleteAtHead();
}
if (index === this.length - 1) {
return this.deleteAtTail();
}
const nodeToBeDeleted = this.getNodeAtIndex(index);
nodeToBeDeleted.prev.next = nodeToBeDeleted.next;
nodeToBeDeleted.next.prev = nodeToBeDeleted.prev;
this.length --;
return;
}
4. Lời kết
Hy vọng với bài viết này, sẽ giúp các bạn có cái nhìn tổng quan về danh sach liên kết đơn, và các thuật toán xung quanh. Happy Coding!!!



