Với công thức chuyển đổi từ kinh vĩ độ sang meshcode được mô tả trong bài viết Chuyển đổi giữa kinh độ, vĩ độ và meshcode Nhật Bản chúng ta có thể tự triển khai các hàm chuyển đổi giữa kinh, vĩ độ và meshcode như sau
Tính meshcode từ kinh vĩ độ
Ý tưởng: do các meshcode của mesh có cấp độ sâu được thừa hưởng lại giá trị của các mesh cấp trên (mesh cấp 3 sẽ có tiền tố là chuỗi số của mesh cấp 1 và mesh cấp 2), nên ta sẽ tạo 1 method có tham số là kinh độ, vĩ độ, mesh level (lat, lon, level) và khi tính giá trị của các mesh cấp độ sâu (cấp 2, 3) thì thực hiện đệ quy dựa trên giá trị của mesh cấp ngay trên. Giá trị đầu vào của lat, lon là các số kiểu float, mesh level nhận các gía trị 1, 2, 3 (hiện tại chỉ tính cho các mesh level này với mục tiêu chủ yếu là hướng đến mesh tiêu chuẩn, chưa đáp ứng tính cho các mesh khu vực 1/2, 1/4, 1/8 cũng như các mesh tích hợp 2x, 5x)
def coords_to_mesh lat, lon, level=3
case level
when 1
return ((lat*3/2).floor * 100 + (lon-100).floor).to_i
when 2
return (coords_to_mesh(lat, lon, 1) * 100 + (lat*12%8).floor * 10 + ((lon-100)*8%8).floor).to_i
when 3
return (coords_to_mesh(lat, lon, 2) * 100 + (lat*120%10).floor * 10 + ((lon-100)*80%10).floor).to_i
else
return "Invalid mesh level"
end
end
Giải thích công thức:
(lat*3/2).floor: 2 chữ số đầu của meshcode cấp 1(lon-100).floor: 2 chữ số sau của meshcode cấp 1(lat*12%8).floor: chữ số đầu của phần dành cho meshcode cấp 2((lon-100)*8%8).floor: chữ số sau của phần dành cho meshcode cấp 2(lat*120%10).floor: chữ số đầu của phần dành cho meshcode cấp 3((lon-100)*80%10).floor: chữ số sau của phần dành cho meshcode cấp 3
Tip: toán tử % với float của Ruby. Nó hoạt động bằng cách chia số thực lấy ra phần nguyên, rồi tính phần dư còn lại bằng của số ban đầu trừ đi tích phần nguyên được tính ra với số chia.
Có nghĩa là: a%b = a - (a/b).floor * b với a float (đảm bảo toán tử / thực hiện phép chia số hữu tỉ thay vì phép chia số nguyên)
Ví dụ :
> 4.5 % 1.25
=> 0.75
> 4.5 - (4.5/1.25).floor * 1.25
=> 0.75
Trong xử lý tính chữ số đầu của phần dành cho meshcode cấp 2 công thức sơ bộ ban đầu là lấy phần dư vĩ độ lat còn lại sau khi bỏ đi vĩ độ ứng với meshcode cấp 1, rồi chia cho khoảng cách vĩ độ của 1 mesh cấp 2 (1/12˚) và lấy phần nguyên. Nếu chuyển đổi thành code sẽ có dạng biểu thức thô như sau:
((lat - (lat*3/2).floor * (2/3)) / (1/12)).floor
= (12 * (lat - (lat / (2/3)).floor * (2/3))).floor
Nhìn vào biểu thức này có thể thấy nếu lấy a = lat, b = 2/3 thì sẽ ra được vế phải dạng a - (a/b).floor * b và có thể rút gọn lại thành lat % (2/3) như vế trái, công thức sẽ trở thành
(12 * (lat % (2/3))).floor
Ngoài ra thêm 1 công thức có thể áp dụng để đơn giản hoá biểu thức là a%b = (ka)%(kb)/k với k là số nguyên . Từ đó (lat % (2/3) có thể biến đổi như sau
(lat % (2/3)
= ((lat*12) % (2/3 * 12) /12
= (lat*12) % 8 / 12
Tổng kết lại ta được công thức tính chữ số đầu tiên của meshcode cấp 2:
(12 * (lat*12) % 8 / 12).floor
= ((lat*12) % 8).floor
Áp dụng tip này cho các biểu thức tính các chữ số meshcode tương tự khác, cuối cùng ta sẽ thu được công thức như được viết trong nội dung method.
Tính kinh vĩ độ của điểm trung tâm 1 mesh
Ý tưởng: mỗi đơn vị meshcode đều tương ứng với 1 khoảng cách vĩ độ, kinh độ nhất định nên đơn giản chỉ cần cộng dồn các vĩ độ, kinh độ từ các meshcode cấp cao xuống dần các meshcode cấp thấp (cấp sâu) se ra toạ độ (vĩ độ, kinh độ) góc tây nam của 1 mesh. Nếu muốn tính toạ độ điểm trung tâm của mesh thì cần cộng thêm 1 nửa khoảng cách vĩ độ cũng như 1 nửa khoảng cách kinh độ giữa 2 mesh liền kề như đã đề cập tại bài viết Chuyển đổi giữa kinh độ, vĩ độ và meshcode Nhật Bản
def mesh_to_sw_coords code, level=3
if (code.to_s.length < (level*2 + 2)) || ![4, 6, 8].include?(code.to_s.length) || (code.to_i == 0)
return "Invalid mesh code"
end
case level
when 1
return code.to_s[0..1].to_f*2/3, code.to_s[2..3].to_f+100
when 2
return (mesh_to_sw_coords(code, 1)[0] + code.to_s[4].to_f/12), (mesh_to_sw_coords(code, 1)[1] + code.to_s[5].to_f/8)
when 3
return (mesh_to_sw_coords(code, 2)[0] + code.to_s[6].to_f/120), (mesh_to_sw_coords(code, 2)[1] + code.to_s[7].to_f/80)
else
return "Invalid mesh level"
end
end
def mesh_to_center_coords code, level=3
return "Invalid mesh code" if code.to_s.length < (level*2 + 2)
case level
when 1
return (mesh_to_sw_coords(code, 1)[0] + 1/3), (mesh_to_se_coords(code, 1)[0] + 1/2)
when 2
return (mesh_to_sw_coords(code, 2)[0] + 1/24), (mesh_to_se_coords(code, 2)[0] + 1/16)
when 3
return (mesh_to_sw_coords(code, 3)[0] + 1/240), (mesh_to_se_coords(code, 3)[0] + 1/160)
else
return "Invalid mesh level"
end
end
Tính kinh vĩ độ của 4 góc 1 mesh
Tại sao lại nảy sinh việc tính toạ độ theo kinh vĩ độ 4 góc của 1 mesh trong khi chỉ cần toạ độ của 1 góc tây nam hoặc toạ độ điểm trung tâm của 1mesh là đã đủ để đại diện cho khu vực của 1 mesh rồi ?
Lý do là có 1 số bào toán thực tế liên quan đến việc xác định 1 mesh có chồng lấn 1 phần hay toàn bộ trong 1 khu vực định trước hay không. Đó là những trường hợp từ 1 khu vực cho trước (hình tròn, đa giác), cần xác định danh sách meshcode mà khu vực đó bao phủ. Do khu vực chỉ định thì hình thù khá đa đạng trong khi các mắt lưới (mesh) thì lại dạng hình gần vuông nên hầu như luôn xảy ra trường hợp các vị trí ở biên của khu vực chỉ định thuộc 1 mesh mà mesh đó chỉ chồng lấn 1 phần với khu vực. Và các thuật toán xác định chồng lấn của 2 hình (thường là đa giác) thì thường cần input là danh sách đỉnh của 2 hình.
Ý tưởng: tính toạ độ các góc từ toạ độ góc tây nam (được tính bởi method mesh_to_sw_coords phía trên). Kinh độ, vĩ độ 2 góc bất kỳ của 1 mesh hoặc là trùng nhau hoặc là lệch nhau 1 khoảng cách bằng khoảng cách kinh độ/ vĩ độ giưã 2 mesh kề nhau. Giá trị có thể tham chiếu tại mục Một số thông số của các cấp meshcode
# north east corner : north = 1, east = 1
# south east corner : north = 0, east = 1
# north west corner : north = 1, east = 0
# south west corner : north = 0, east = 0
def mesh_to_corner_coords code, north, east, level=3
return "Invalid mesh code" if code.to_s.length < (level*2 + 2)
case level
when 1
return (mesh_to_sw_coords(code, 1)[0] + north*2/3), (mesh_to_sw_coords(code, 1)[1] + east)
when 2
return (mesh_to_sw_coords(code, 2)[0] + north/12), (mesh_to_sw_coords(code, 2)[1] + east/8)
when 3
return (mesh_to_sw_coords(code, 3)[0] + north/120), (mesh_to_sw_coords(code, 3)[1] + east/80)
else
return "Invalid mesh level"
end
end
def mesh_to_square_coords code, level=3
[
mesh_to_corner_coords(code, 0, 0, level),
mesh_to_corner_coords(code, 0, 1, level),
mesh_to_corner_coords(code, 1, 0, level),
mesh_to_corner_coords(code, 1, 1, level)
]
end
1 ví dụ thực tế là kiểm tra 1 mesh có chồng lấn với khu vực rìa hình tròn tâm A bán kính R cho trước hay không. Khi đó sau khi lấy được danh sách toạ độ 4 góc của mesh có thể kiểm tra từng góc đó có nằm trong phạm vi hình tròn hay không bằng cách tính khoảng cách từ góc đến tâm A rồi so sánh với bán kính R. Nếu khoảng cách từ góc đến tâm A lớn hơn R thì tức là góc nằm ngoài hình tròn, ngược lại khoảng cách từ góc đến tâm A nhỏ hơn R thì góc nằm trong hình tròn.
Công thức tính khoảng cách giữa 2 điểm dựa trên kinh, vĩ độ có thể tham khảo Haversine formula với sample implement đơn giản cho Ruby tại đây hoặc có thể sử dụng API của các thư viện như Google Map API
Khi kiểm tra cả 4 góc sẽ xảy ra các trường hợp sau
- Cả 4 góc nằm ngoài hình tròn → mesh hoàn toàn nằm ngoài hình tròn
- Có 1 số góc nằm ngoài hình tròn và số góc còn lại nằm trong hình tròn → chồng lấn 1 phần với hình tròn
- Cả 4 góc nằm trong hình tròn → mesh hoàn toàn nằm trong hình tròn
Danh sách meshcode "hàng xóm"
Bài toán: xác định danh sách meshcode hàng xóm cách 1 mesh cho trước không quá N đơn vị mesh cùng cấp mỗi chiều bắc-nam, đông-tây
Ý tưởng: nếu để ý hình ảnh bản đồ Nhật Bản hiển thị dưới dạng mesh cấp 1 thì sẽ nhận thấy các mesh liền kề có meshcode phần kinh độ hoặc vĩ độ chênh nhau 1.
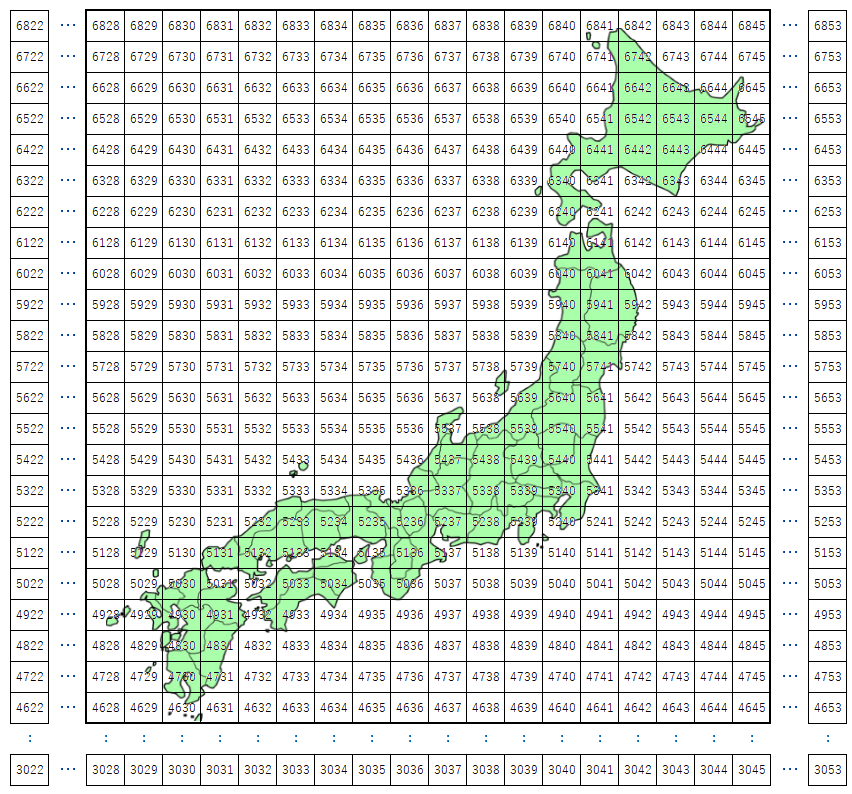
Tuy nhiên cho quá trình chia mesh cấp 1 thành mesh cấp 2 không phải là chia mỗi chiều thành 10 phần mà chỉ là chia thành 8 phần nên khi list toàn bộ danh sách meshcode cấp 2 (6 chữ số) của Nhật bản ra sẽ không thấy được dải số liên tục (2 chữ số cuối không bao giờ là 8 hay 9). Do đó việc dò meshcode của các mesh hàng xóm sẽ không còn đơn thuần là tăng giảm dần 1 đơn vị mesh nữa.
Ví dụ: 1 mesh cấp 2 cho trước có chữ số cuối cùng (chữ số đại diện cho phần kinh độ) là 0 sẽ có mesh liền kề phía Tây (trái) với meshcode mà chữ số cuối cùng là 7 (chứ không phải là 9 như khi thực hiện -1) Việc tính toán thực ra vẫn có thể nhưng sẽ phức tạp hơn 1 chút.
Nhưng ngược lại khoảng cách giữa tâm 2 mesh liền kề luôn đảm bảo là 1 đơn vị khoảng cách mesh cấp tương ứng (ví dụ với mesh tiêu chuẩn là 1/120˚ cho khoảng cách hướng bắc nam và 1/80˚ cho khoảng cách hướng đông tây). Kể cả không phải là tâm của mesh mà chỉ cần là 1 điểm bất kỳ trong mesh thì nếu thực hiện cộng hoặc trừ 1 đơn vị khoảng cách mesh để ra toạ độ 1 điểm mới thì chắc chắc điểm mới đó thuộc mesh liền kề. Mở rộng hơn: thực hiện cộng hoặc trừ N đơn vị khoảng cách mesh (N là số nguyên) từ 1 toạ độ gốc cho trước sẽ cho ra 1 điểm mới nằm trong 1 mesh mới cách mesh của toạ độ gốc N đơn vị mesh theo chiều bắc-nam hoặc đông-tây.
Lợi dụng tính chất này ta có thể tính toàn bộ các điểm "hàng xóm" bằng cách cộng/trừ 1~N đơn vị khoảng cách mesh từ tạo độ gốc, sau đó convert tất cả toạ độ các điểm "hàng xóm" này thành ngược trở lại meshcode để ra danh sách meshcode "hàng xóm"
Implement method list danh sách tạo độ điểm "hàng xóm" với ruby
def neighbor_coords src_lat, src_lon, mesh_dist=1, level=3
lat_degree_step_by_level = {
1 => 2.to_f/3,
2 => 1.to_f/12,
3 => 1.to_f/120
}
lon_degree_step_by_level = {
1 => 1,
2 => 1.to_f/8,
3 => 1.to_f/80
}
lat_range = (-mesh_dist..mesh_dist).map{|dist| src_lat + dist * lat_degree_step_by_level[level]}
lon_range = (-mesh_dist..mesh_dist).map{|dist| src_lon + dist * lon_degree_step_by_level[level]}
neighbor = []
lat_range.product(lon_range)
end
※ Method trên cho ra danh sách điểm bao gồm bản thân điểm gốc nên nếu muốn thực sự chỉ lấy điểm "hàng xóm" thì cần thêm 1 bước phụ là loại bỏ điểm gốc khỏi kết quả
Cách thức tính này có ưu điểm là nội dung method ngắn hơn nhưng nhược điểm là phải thực hiện phép convert sang meshcode với từng toạ độ điểm "hàng xóm". Do đó có thể dùng trong trường hợp N không lớn nhưng nếu N đủ lớn thì nên xem xét hướng implement khác.
Ứng dụng thực tế: tìm danh sách meshcode tiêu chuẩn trong khu vực được xác định bởi hình tròn bán kính 5km tâm A. Do khoảng cách meshcode tiêu chuẩn là ~1km, khi đó ta có thể thực hiện hàm xác định danh sách meshcode tiêu chuẩn hàng xóm cách tâm A không quá 5 đơn vị meshcode tiêu chuẩn. Danh sách tìm được (tính cả mesh của tâm A) sẽ là 1 lưới hình vuông kích cỡ 5*2+1 = 11 mesh tiêu chuẩn mỗi chiều, cho ra 11*11 = 121 mesh là các mesh hàng xóm và mesh của bản thân tâm A.



