CuPy

CuPy là một thư viện array open-source, áp dụng kiểu dữ liệu multi-dimensional array (N-dimensional array hay còn gọi là ndarrays) trên khả năng tính toán song song ưu việt của các core trong card đồ họa NVIDIA. Hay nói cách đơn giản là CuPy là NumPy nhưng được tính toán với GPU.
Cụ thể hơn, data được sẽ được sao chép từ CPU (host) đến GPU (device) để thực hiện tính toán.

CuPy hoàn toàn tương thích với NumPy, trong hầu hết các trường hợp CuPy có thể thay thế numpy bằng cupy. CuPy cũng hỗ trợ nhiều phương thức, indexing, kiểu dữ liệu, broadcasting... Các bạn có thể tham khảo chi tiết tại đây

Installation

    pip install cupy-cuda<vesion>

Lưu ý: Hãy cài đúng phiên bản CUDA đang sử dụng nhé

Basic Use

import numpy as np
import cupy as cp

Như đã nói ở trên cupy.ndarray là phiên bản tương thích của numpy.ndarray trên GPU. Điểm khác biệt ở đây là cupy.ndarray dữ liệu được cấp phát trên bộ nhớ GPU

x_gpu = cp.array([1, 2, 3])
l2_gpu = cp.linalg.norm(x_gpu)

Ví dụ:

array = cp.arange(10).reshape((2,5))
print(repr(array))
print(array.dtype)
print(array.shape)

array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]])
int64
(2, 5)

array_cpu = np.arange(10)
array_gpu = cp.asarray(array_cpu)
print('CPU:', array_cpu)
print('GPU:', array_gpu)
print(array_gpu.device)

chuyển đổi dữ liệu từ CPU sang GPU

cpu: [0 1 2 3 4 5 6 7 8 9]
gpu: [0 1 2 3 4 5 6 7 8 9]
<CUDA Device 0>

Khi run, CuPy sẽ compile CUDA function và cache để có thể sử dụng lại => nhanh hơn so với lần chạy đầu tiên

Kernels

Ngoài các tính năng tương tự NumPy như trên, CuPy còn cho phép người dùng tự định nghĩa kernels sử dụng với 3 kiểu CUDA kernel: elementwise kernel, reduction kernel và raw kernel

Elementwise kernel

Elementwise kernel sẽ bao gồm 4 thành phần: danh sách input, danh sách output, function body code và tên kernel. Ví dụ

squared_func = cp.ElementwiseKernel(
    'float32 x, float32 y', #input  
    'float32 z', #output
    'z = (x-y)*(x-y)', #function
    'squared_func' #name
)

x = cp.arange(10, dtype=np.float32).reshape(2, 5)
y = cp.arange(5, dtype=np.float32)
squared_func(x, y)

array([[ 0., 0., 0., 0., 0.],
[25., 25., 25., 25., 25.]],
dtype=float32)

Điểm khá thú vị là CuPy kernel có support Type-generic như trong C# và Java . Để hiểu kỹ hơn các bạn có thể tham khảo bài này, nhưng nhìn chung với Generics bạn không cần định nghĩa cụ thể kiểu dữ liệu khi truyền vào function, kiểu dữ liệu sẽ được đại diện với tham số T

Ví dụ:

squared_diff_generic = cp.ElementwiseKernel(
     'T x, T y',
     'T z',
     'z = (x - y) * (x - y)',
     'squared_diff_generic')
     
x = cp.arange(10, dtype=np.float32).reshape(2, 5)
y = cp.arange(5, dtype=np.float32)
squared_diff_generic(x, y)

Reduction kernel

Loại kernel thứ 2 là Reduction kernel với Map-Reduce có thể tự định nghĩa

l2norm_kernel = cp.ReductionKernel(
     'T x',  # input params
     'T y',  # output params
     'x * x',  # map
     'a + b',  # reduce
     'y = sqrt(a)',  # post-reduction map
     '0',  # identity value
     'l2norm'  # kernel name
)

x = cp.arange(10, dtype=np.float32).reshape(2, 5)  
l2norm_kernel(x, axis=1)

array([ 5.477226 , 15.9687195], dtype=float32)

Raw kernel

Với RawKernel, bạn có toàn quyền kiểm soát đối với grid size,* block size*, kích cỡ memory sử dụng và stream

add_kernel = cp.RawKernel(r'''
extern "C" __global__
void my_add(const float* x1, const float* x2, float* y) {
    int tid = blockDim.x * blockIdx.x + threadIdx.x;
    y[tid] = x1[tid] + x2[tid];
}
''', 'my_add')

Như trên, ta có hàm tính toán cộng array add_kernel tự định nghĩa

x1 = cp.arange(25, dtype=cp.float32).reshape(5, 5)
x2 = cp.arange(25, dtype=cp.float32).reshape(5, 5)
y = cp.zeros((5, 5), dtype=cp.float32)
add_kernel((5,), (5,), (x1, x2, y))

array([[ 0., 2., 4., 6., 8.],
[10., 12., 14., 16., 18.],
[20., 22., 24., 26., 28.],
[30., 32., 34., 36., 38.],
[40., 42., 44., 46., 48.]], dtype=float32)

Raw kernel còn có thể hoạt động với cả chuỗi số phức

complex_kernel = cp.RawKernel(r'''
#include <cupy/complex.cuh>
extern "C" __global__
void my_func(const complex<float>* x1, const complex<float>* x2,
            complex<float>* y, float a) {
    int tid = blockDim.x * blockIdx.x + threadIdx.x;
    y[tid] = x1[tid] + a * x2[tid];
}
''', 'my_func')

 x1 = cp.arange(25, dtype=cp.complex64).reshape(5, 5)
 x2 = 1j*cp.arange(25, dtype=cp.complex64).reshape(5, 5)
 y = cp.zeros((5, 5), dtype=cp.complex64)
  complex_kernel((5,), (5,), (x1, x2, y, cp.float64(2.0)))  # grid, block and arguments

y = array(
[[ 0.+0.j, 1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j],
[ 5.+0.j, 6.+0.j, 7.+0.j, 8.+0.j, 9.+0.j],
[10.+0.j, 11.+0.j, 12.+0.j, 13.+0.j, 14.+0.j],
[15.+0.j, 16.+0.j, 17.+0.j, 18.+0.j, 19.+0.j],
[20.+0.j, 21.+0.j, 22.+0.j, 23.+0.j, 24.+0.j]], dtype=complex64)

Computation Speed Comparison

Để demo sức mạnh tính toán của CuPy, tôi sẽ thử các phương pháp tính toán theo từ đơn giản nhất là Python. Phép tính toán cũng không quá phức tạp, chỉ bao gồm cộng trừ nhân chia thông thường. Cụ thể thực hiện lần lượt phép tính +, - và lấy căn bậc hai với 2 array độ lớn 1.000.000 phần tử

import numpy as np
import cupy as cp

Python thuần

%% time
# Pure Python

arr_1 = range(1000000)
arr_2 = range(99,1000099)

a_sum = []
a_prod = []
sqrt_a1 = []

for i in range(len(arr_1)):
    a_sum.append(arr_1[i]+arr_2[i])
    a_prod.append(arr_1[i]*arr_2[i])
    sqrt_a1.append(arr_1[i]**0.5)
    
arr_1_sum = sum(arr_1)

CPU times: user 1.06 s, sys: 55.6 ms, total: 1.11 s
Wall time: 1.12 s

Với python thông thường, quá trình này mất đến hơn 1s, không có gì lạ khi phải thực hiện phép toán với từng phần tử trong list.

Python kết hợp NumPy

%%time
# Python converted to NumPy
arr_1 = range(1000000)
arr_2 = range(99,1000099)

arr_1, arr_2 = np.array(arr_1) , np.array(arr_2)

a_sum = arr_1 + arr_2
a_prod = arr_1 * arr_2
sqrt_a1 = arr_1 ** .5
arr_1_sum = arr_1.sum()

CPU times: user 377 ms, sys: 74 ms, total: 451 ms
Wall time: 450 ms

Khi list được chuyển đổi sang dạng numpy array, tốc độ tính toán nhanh hơn hẳn. Nguyên nhân do kiểu dữ liệu ndarrays của numpy thực hiện phép tính theo dạng vector hóa.

Numpy thuần

%%time
# NumPy
arr_1 = np.arange(1000000)
arr_2 = np.arange(99,1000099)

a_sum = arr_1 + arr_2
a_prod = arr_1 * arr_2
sqrt_a1 = arr_1 ** .5
arr_1_sum = arr_1.sum()

CPU times: user 50.2 ms, sys: 0 ns, total: 50.2 ms
Wall time: 49.4 ms

Tốc độ lúc này cũng được tối ưu với kiểu NumPy với khả năng tính toán x10 thật đáng sợ

CuPy

Và đến với nhân vật chính hôm nay: thư viện CuPy

%%time
arr_1 = cp.arange(1000000)
arr_2 = cp.arange(99,1000099)

a_sum = arr_1 + arr_2
cp.cuda.Stream.null.synchronize()
a_prod = arr_1 * arr_2
cp.cuda.Stream.null.synchronize()
sqrt_a1 = arr_1 ** .5
cp.cuda.Stream.null.synchronize()
arr_1_sum = arr_1.sum()
cp.cuda.Stream.null.synchronize()

CPU times: user 2.04 ms, sys: 2.83 ms, total: 4.87 ms
Wall time: 4.58 ms

Tốc độ tính toán chỉ 4.87ms, gấp 10 lần so với NumPy với GPU Tesla T4 (Colab obviously)

Plot ra 1 chút cho dễ hình dung

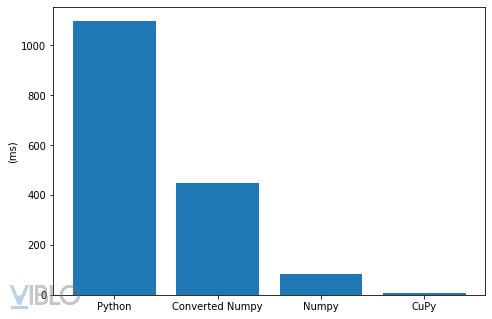
Đồng thời, theo thống kê của RAPIDS AI CuPy có tốc độ nhanh hơn nhiều lần NumPy với các thuật toán khác nhau, đặc biệt với các array lớn

Conclusion

CuPy nhanh đến vậy tại sao chúng ta không sử dụng nó luôn mà vẫn đa phần dùng NumPy?

Thứ nhất, bạn phải có GPU mới sử dụng được CuPy, khá hiển nhiên
Thứ hai, CuPy cho thấy sự ưu việt với nhiều dữ liệu ( > 10.000.000 điểm dữ liệu). Nếu tập data của bạn nhỏ hoặc phép tính toán quá đơn giản , sử dụng CuPy không khác gì lấy dao mổ trâu để giết gà Bạn có thể giảm số chiều của ví dụ trên xuống dưới 1.000 sẽ thấy ngay được sự cồng kềnh khi tính toán với CuPy
Thứ ba, khi kiểu dữ liệu quá lớn so với nhu cầu có thể gây tốn tài nguyên cấp phát của GPU (parallel computing, duh?)