Chào mọi người, hôm nay mình sẽ giới thiệu với mọi người 1 phương pháp vô cùng cần thiết trong bước tiền xử lý dữ liệu: Scaling và Normalization

I. Tại sao cần scaling và normalization?

    Khi xử lý dữ liệu thô, chúng ta sẽ gặp rất nhiều các dạng dữ liệu lạ nên đôi khi rất khó để phân tích và tìm ra insights. Một cách tiếp cận đơn giản là biến đổi dữ liệu, mục tiêu là đưa dữ liệu về một phân phối chuẩn (normal (Gaussian) distribution), ví dụ như bell curve. Dữ liệu có dạng phân phối chuẩn giúp mô hình học được tốt hơn và đưa ra dự đoán chính xác và sát với kết quả ta mong muốn hơn.

    Khác biệt giữa scaling và Normalization

    Hẳn ban đầu mới tiếp xúc, các bạn cũng có chút nhầm lẫn giữa 2 loại nhỉ (hoặc chỉ mỗi mình ). Một trong những lý do gây ra hiểu nhầm là các thuật ngữ đôi khi được sử dụng thay thế cho nhay và hơn hết, nếu chỉ lướt qua, ta sẽ thấy chúng rất giống nhau, về hình thức và mục đích. Trong cả 2 trường hợp, ta đều biến đổi dữ liệu để thu được những thuộc tính hữu ích. Điểm khác biệt ở đây là:

• Scaling thay đổi khoảng giá trị của dữ liệu
• Normalization thay đổi hình dạng phân phối của dữ liệu

    Let's take a closer look ->

II. Scaling

    Scaling là biến đổi khoảng giá trị của dữ liệu về một khoảng đặc biệt như 0-100 hay 0-1, thường là 0-1. Trong một số thuật toán Machine Learning mà khoảng cách giữa các điểm dữ liệu là quan trong, như SVM hay KNN, thì việc scale dữ liệu là vô cùng quan trọng, vì mỗi thay đổi nhỏ của dữ liệu cũng mang đến kết quả khó đoán trước.

    Giả sử trong dữ liệu về cân nặng 1 người, có 2 loại dữ liệu là kg và pound. Khi chúng ta sử dụng trực tiếp những giá trị này với SVM hoặc KNN, thuật toán sẽ hiểu sự 1kg = 1pound, nhưng điều đó không đúng trong thực tế (1pound = 0.45359237kg). Qua ví dụ trên, chắc mọi người cũng đã hiểu được tầm quan trọng của việc scale dữ liệu.

    Scale dữ liệu cần thực hiện trên cùng mục đích sử dụng của thước đo (tiền - tiền, chiều cao - chiều cao,...), chứ hiển nhiên ta ko thể scale cân nặng với chiều cao, vì giữa chúng cơ bản không có sự liên quan mật thiết.

    Một số loại scale thông dụng:

1.1 Simple Features Scaling

    $$X_{new} = \frac{X_{old}}{X_{max}}$$

    Phương pháp đơn giản là lấy các giá trị trên cùng 1 features chia cho giá trị lớn nhất của features đó. Khoảng giá trị nhận lại mong muốn thường từ 0 đến 1.

    Chính vì tính đơn giản của phương pháp, nên thường được sử dụng với features mà tất cả giá trị của features đó thuộc khoảng $(-\infty, 0]$ hoặc $[0, +\infty)$

    Ta bắt gặp phương pháp này nhiều nhất (maybe), trong xử lý ảnh, khi mà ta thường chia giá trị của các pixel trên 1 bức ảnh cho 255 (giá trị lớn nhất của 1 pixel)

1.2 Min-Max Scaling

    $$X_{new} = \frac{X_{old} - X_{min}}{X_{max} - X_{min}}$$

    Mục tiêu của phương pháp là đưa các giá trị về gần hơn giá trị mean của features. Phương pháp này đưa các giá trị về 1 khoảng đặc biệt, thường là $[0, 1]$ hoặc $[-1, 1]$. Một trong những hạn chế của phương pháp này là khi áp dụng với một khoảng giá trị nhỏ, ta sẽ thu được độ lệch chuẩn nhỏ hơn, điều này làm giảm weight của các outliers trong dữ liệu.

    ##1.3 Ví dụ

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import minmax_scale

# set seed for reproducibility
np.random.seed(0)

# generate 1000 data points randomly drawn from an exponential distribution
original_data = np.random.exponential(size = 1000)

# mix-max scale the data between 0 and 1
scaled_data = minmax_scale(original_data)

# plot both together to compare
fig, ax=plt.subplots(1,2)
sns.distplot(original_data, ax=ax[0], color='y')
ax[0].set_title("Original Data")
sns.distplot(scaled_data, ax=ax[1])
ax[1].set_title("Scaled data")
plt.show()

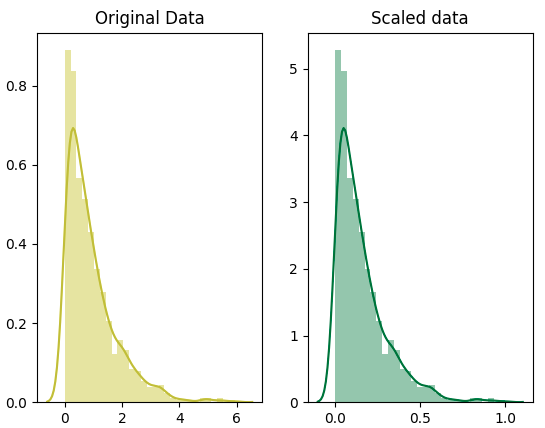
    Qua ví dụ, khẳng định scaling chỉ làm thay đổi khoảng giá trị chứ không làm thay đổi hình dạng phân phối dữ liệu là chính xác.

II. Normalization

    Như đã nói ở trên, scaling chỉ làm thay đổi khoảng giá trị dữ liệu, normalization là 1 cách thay đổi triệt để hơn. Mục đích là biến đổi dữ liệu với kì vọng thu được 1 phân phối chuẩn cho dữ liệu đó

    Normal distribution: Also known as the "bell curve", this is a specific statistical distribution where a roughly equal observations fall above and below the mean, the mean and the median are the same, and there are more observations closer to the mean. The normal distribution is also known as the Gaussian distribution.

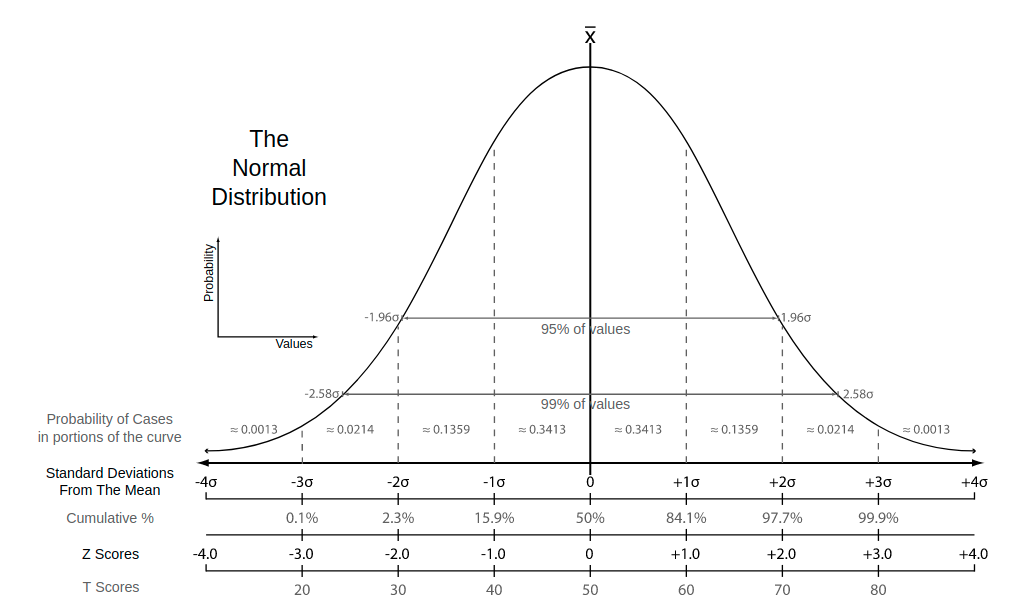
    Note: Định nghĩa trên là theo khái niệm của thống kê. Có nhiều loại normalization khác nhau. Trên thực tế, min-max scaling cũng được coi là một kiểu normalization. Trong Machine Learning, một số loại normalization sau đây được sử dụng phổ biến nhất

2.1 Standardization hay Z-score normalization

    $$X_{new} = \frac{X_{old} - X_{mean}}{\sigma}$$

    Với $\sigma$ là độ lệch chuẩn (standard deviation)

    Sau bước biến đổi, ta sẽ thu được tập giá trị mới mean bằng 0 và std bằng 1 (dễ dàng chứng minh). Phương pháp này có ích với những dữ liệu có outlier mà bạn lại không muốn loại bỏ hoàn toàn những ảnh hưởng của nó.

    Standardization được sử dụng rộng rãi trong SVM, logistics regression và neural networks.

2.2 Mean Normalization

    $$X_{new} = \frac{X_{old} - X_{mean}}{X_{max} - X_{min}}$$

    Phương pháp đơn giản này nhìn quá có vẻ giống nhưng thực tế nó khác với min-max scaling và Standardization.

    Sau khi áp dụng ta sẽ thu được một phân phối với mean bằng 0

2.3 Box-Cox Normalization

    $$\mathrm y_i^{(\lambda)} = \begin{cases} \frac{y_i^{\lambda} - 1}{\lambda} & \text{if } \lambda \neq 0 \\ \ln(y_i) & \text{if} \lambda = 0 \end{cases}$$

    Box-cox thường được sử dụng để ổn định variance (loại bỏ các phương sai bị thay đổi) và biến đổi non-normal dependent variables thành normal shape.

    Để hiểu rõ hơn về phương pháp này, các bạn có thể đọc tại đây

    Ví dụ sau đây sử dụng box-cox normalization được cài đặt sẵn trong thư viện scipy.

# for Box-Cox Transformation
from scipy import stats

# normalize the exponential data with boxcox
normalized_data = stats.boxcox(original_data)

# plot both together to compare
fig, ax=plt.subplots(1,2)
sns.distplot(original_data, ax=ax[0], color='y')
ax[0].set_title("Original Data")
sns.distplot(normalized_data[0], ax=ax[1])
ax[1].set_title("Normalized data")
plt.show()

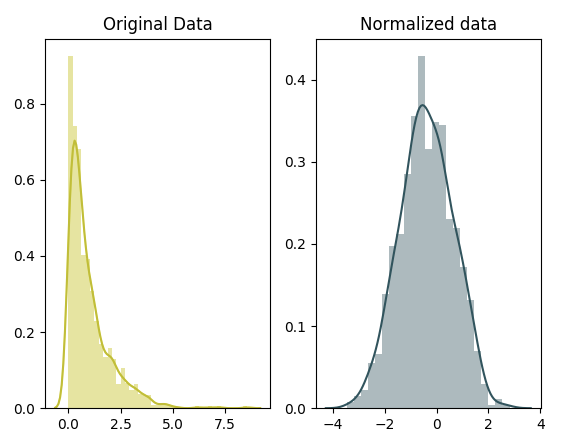
III. Một số phương pháp biến đổi dữ liệu khác

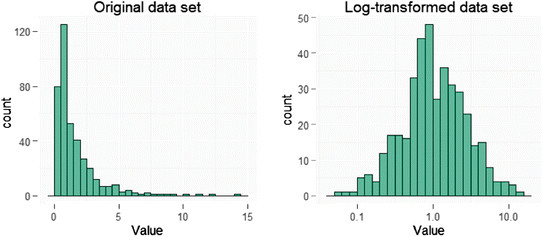
3.1 Log Transformation

    $$x = \log(x)$$

    Phương pháp này được sử dụng nhất khi dữ liệu bị lệch (không đối xứng). Kết quả thu được có kì vọng làm dữ liệu đối xứng hơn.

3.2 Unit Vector Transformation

    $$X_{new} = \frac{X_{old}}{||x||}$$

    Với $||\overrightarrow{x}|| = \sqrt{\sum{x_i^2}}$, $\overrightarrow{x}(x_1, x_2,..., x_n)$

    Với phương pháp này, ta tự chia các giá trị của vector với độ dài của chính nó, khi đó, độ dài của vector bằng 1. Phương pháp này dùng để chuẩn hóa độ dài của vector mà không làm thay đổi hướng của nó.

IV. Kết luận

    Như vậy, ta đã biết được normalization là một phương pháp hữu ích khi dữ liệu của bạn không theo phân phối Gaussian. Normalization thay đổi các giá trị của dữ liệu với mục đích chính để thu được 1 phân phối dữ liệu tốt hơn cho các thuật toán học máy.

    Scaling hữu ích khi muốn so sánh 2 thang đo khác nhau với mục đích sử dụng tương đương. Thường được sử dụng cho các bài toán mà khoảng cách giữa các điểm dữ liệu mang tính quan trọng, đưa đến sự cân bằng giữa các điểm dữ liệu. Vì khi một biến có trọng số lớn hơn các biến khác, mô hình sẽ tập trung vào những giá trị đó.

    Các bạn có thể thực hành tại những kiến thức trên tại kaggle

    Cảm ơn các bạn đã dành thời gian đọc bài viết của mình. Hẹn gặp lại các bạn trong bài viết tiếp theo. See ya!! (KxSS)

Tài liệu tham khảo

1. Feature Scaling for Machine Learning: Understanding the Difference Between Normalization vs. Standardization
2. Power transform
3. Scaling vs. Normalizing Data