Mở bài

    Vấn đề về adversarial attacks chắc hẳn đã không còn xa lạ sau khi đọc bài kia của mình rồi nhỉ Đó là khi một ảnh có thể bị thay đổi đôi chút sao cho người nhìn không nhận ra khác nhau, nhưng mô hình thì lại đưa ra dự đoán sai.

    Vậy ngoài các cách phòng thủ trong bài trên ra còn những phương pháp nào nữa? Một cách chúng ta có thể làm là xử lý luôn trường hợp xấu nhất, bằng cách train với toàn bộ data đã bị dịch chuyển trong $\epsilon$-ball xung quanh data sạch, vậy thì các tấn công không thể làm gì được nữa. Bạn có thể tưởng tượng nó gần giống như adversarial training, nhưng thay vì mất công tìm ra adversarial example mà mô hình dự đoán sai, chúng ta chọn bừa một điểm trong khoảng tấn công cho phép bất kể có thành công hay không. Sau nhiều lần sample như vậy thì mô hình sẽ học được rằng tất cả những ảnh gần giống ảnh gốc cũng phải dự đoán ra giống ảnh gốc.

    Đơn giản đúng không? Vậy giờ chúng ta vào nội dung chính của bài nhé!

Existing works

    Việc thêm nhiễu vào mô hình không có gì là mới cả. Với quá trình training bình thường, việc augment data bằng cách thêm nhiễu là điểu gần như mặc định luôn làm. Ngoài ra, thêm nhiễu vào label cũng được thường xuyên sử dụng: hoặc là thêm nhiễu không, hoặc là sử dụng label smoothing: khi chúng ta cho ground truth label không phải là one-hot mà là $[0.9,0.01,0.01,\dots,0.01]$. Tất cả những phương pháp trên được sử dụng để cho mô hình tăng khả năng generalization, học được data được lấy ở những điều kiện khác nhau (giúp generalize ra data ở ngoài dataset), và để giảm độ tự tin của mô hình (từ đó giảm overfitting). Đó cũng là lý do tại sao knowledge distillation hoạt động: khi học với các pseudolabel, mô hình sẽ học được những kiến thức riêng theo model giáo viên, và sẽ generalize tốt hơn so với việc học vẹt true label.

    Tuy nhiên, ít ai để ý rằng một hiệu quả vô tình của việc thêm nhiễu là làm giảm adversarial vulnerability, như mình đã đề cập ở trước. Bằng cách học được việc các data tương tự với data sạch cũng phải đưa ra prediction giống thế, cách augmentation này giúp cho mô hình trở nên khó bị tấn công hơn. Tuy nhiên, có một điểm khác nữa là các phương pháp sau đây sử dụng việc thêm nhiễu cả vào các output ở giữa mô hình, và cả trong tensor trọng số của mô hình nữa!

PixelDP

    Được viết bởi Lecuyer et. al, Columbia University, PixelDP mô tả một mô hình được thiết kế để tránh bị tấn công nhờ các matrix bounds và lý thuyết của differential privacy. Cụ thể về differential privacy thì rất dài và lằng nhằng nên mình đã viết một bài riêng cho chủ đề này

    Tóm tắt lại công thức của DP trong trường hợp tổng quát, chúng ta có: một thuật toán randomized $A$ lấy một input $d$ và trả về một kết quả trong range $O$ được gọi là $(\varepsilon,\delta)$-DP nếu

    $$\mathbb{P}[A(d)\in S]\le e^\varepsilon\mathbb{P}[A(d')\in S]+\delta$$

    với mọi $\rho(d,d')\le 1$ và $S\subseteq O$, $\rho$ là một distance metrics nào đó, ví dụ như $p$-norm $\Vert\mathbf{x}\Vert_p=\left(\sum_i|x_i|^p\right)^{1/p}$.

Tác dụng của Differential Privacy

    PixelDP xử lý một setting phổ biến khi các layer đưa ra một non-negative representation - ví dụ, data ảnh thường được normalize về khoảng $(0, 1)$, hoặc các lớp Linear thường đều được đưa qua lớp ReLU/softmax. Chúng ta có một bổ đề giới hạn độ thay đổi đầu ra của mô hình (possible misclassification) phụ thuộc vào độ thay đổi đầu vào (adversarial perturbation):

    Bổ đề: Với $A(x)\in[0,b], b\in\mathbb{R}^+$ là một hàm $(\varepsilon,\delta)$-DP, thì:

    $$\mathbb{E}[A(x)]\le e^\varepsilon\mathbb{E}[A(x')]+b\delta \;\forall x,x':\Vert x-x'\Vert_p\le1.$$

    Chứng minh: Phần quan trọng nhất của chứng minh bổ đề trên nằm ở cách chúng ta định nghĩa expected value:

    $$\begin{aligned} \int^b_0\mathbb{P}[A(x)>t]dt &=\int^b_0\int^b_tf_A(x)dxdt\\ &=\int_0^b\int_0^xf_A(x)dtdx & (*)\\ &=\int_0^bxf_A(x)dx\\ &=\mathbb{E}[A(x)] \end{aligned}$$

    Trong đó, $f_A(x)$ là probability distribution function của $A(x)$, và bước $(*)$ là việc đổi thứ tự tích phân theo vùng được tích phân:

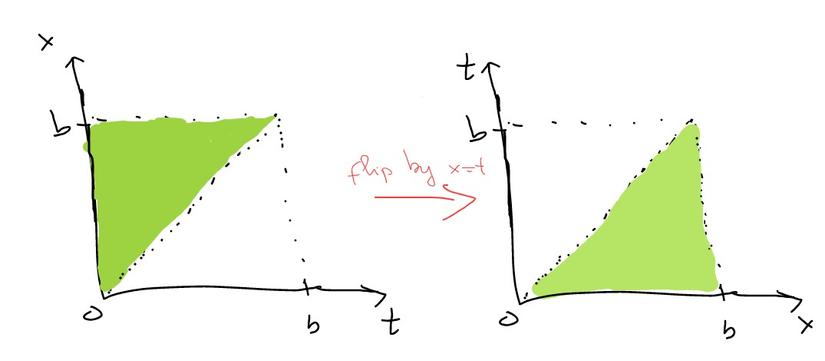
    Từ đó và định nghĩa trên của DP, ta có:

    $$\mathbb{E}[A(x)]\le e^\varepsilon\left(\int^b_0\mathbb{P} [A(x')>t]dt\right) + \int^b_0\delta dt = e^\varepsilon\mathbb{E}[A(x')] + b\delta.$$

    Trường hợp đặc biệt của ảnh được normalize hoặc đầu ra probability là khi $b=1$. Giờ cho $A(x)$ là một hàm $(\varepsilon,\delta)$-DP đưa ra probability distribution trong bài toán classification, chúng ta có thể giới han được xác suất tấn công thành công của một mô hình nếu chúng ta có thể đảm bảo một robust gap giữa class đúng và tất cả các class còn lại:

    $$\mathbb{E}[A_k(x)] > e^{2\varepsilon}\max_{i\ne k}\mathbb{E}[A_i(x)] + (1+e^\varepsilon)\delta$$

    thì

    $$\mathbb{E}[A_k(x')] > \max_{i\ne k}\mathbb{E}[A_i(x')] \;\forall x':\Vert x-x'\Vert_p\le1.$$

    Phần chứng minh khá đơn giản và để lại cho bạn đọc cho đỡ loãng bài Chúng ta có thể scale $p$-norm difference của ảnh gốc và ảnh đã attack từ 1 thành một giá trị bất kỳ bằng DP composition bound đã có trong bài DP kia.

    Từ công thức trên, chúng ta có thể suy ra rằng với phương pháp này, sau khi đảm bảo yêu cầu DP, chúng ta có thể tính robust gap kia để giới hạn được độ lớn của adversarial perturbation; và việc expected value được sử dụng trong công thức cho chúng ta thấy, trong quá trình inference chúng ta sẽ sử dụng trung bình của nhiều lần inference khác nhau làm kết quả cuối cùng.

Đảm bảo yêu cầu Differential Privacy

    Đơn giản thôi, thêm một noise layer vào đâu đó trong mô hình sao cho bước đó đảm bảo $(\varepsilon,\delta)$-DP, và tính chất postprocessing immunity của DP sẽ xử lý hết phần còn lại

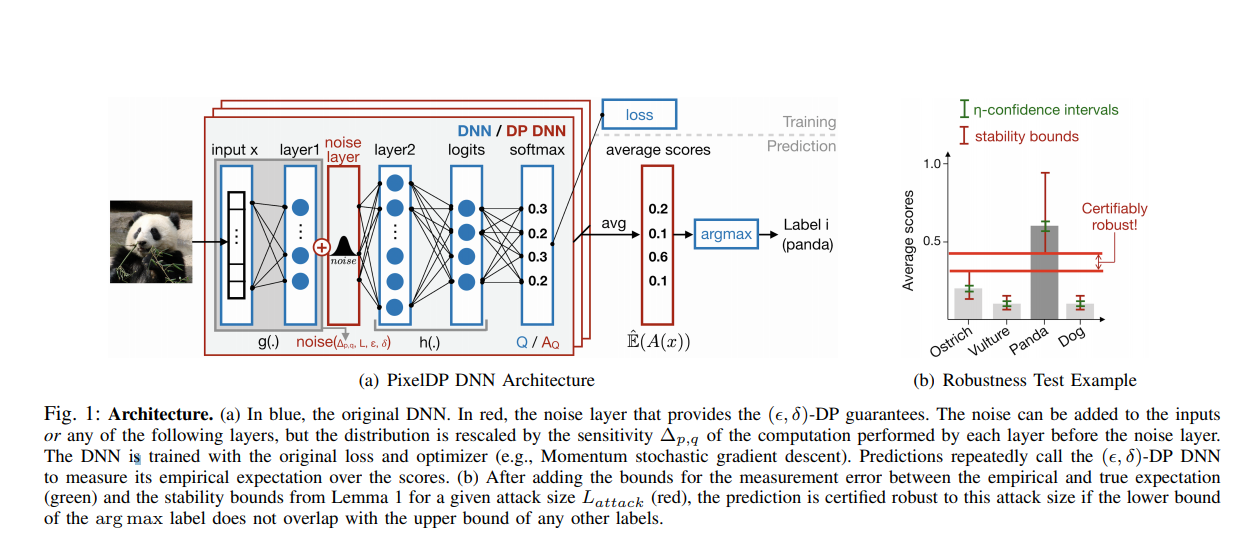
    Tuy nhiên, phần khó nhất của việc đảm bảo yêu cầu DP là phải giới hạn được sensitivity của mô hình tại điểm đó. Noise layer của chúng ta đặt càng sâu trong mô hình thì càng khó ước lượng và giới hạn sensitivity của mô hình tại điểm đó, do độ phức tạp của tính toán tại điểm đó càng ngày càng cao. Để nhắc lại, sensitivity của một hàm được định nghĩa là:

    $$\Delta_{p,q}f=\max_{\Vert x-x'\Vert_p\le 1}\Vert f(x) - f(x')\Vert_q.$$

    Một vài vi trí có thể đặt lớp nhiễu có thể kể đến:

• Thêm nhiễu ngay vào đầu vào: do chưa có xử lý gì data nên sensitivity bằng chính xác 1 nếu $p=q$.
• Thêm nhiễu vào ngay sau lớp Linear đầu tiên: tạm bỏ qua bias cho đơn giản, sensitivity chính là định nghĩa của $\Vert W\Vert_{p,q}$, với $W$ là weight của lớp Linear đầu tiên đó, do chúng ta có thể hiểu norm ở đây theo hướng operator norm.
• Thêm nhiễu vào sâu nữa: chúng ta có thể sử dụng composition bound và cứ nhân tới các privacy bound, nhưng kết quả sẽ càng ngày càng lỏng quá mức. Có một số phương pháp giúp giảm sensitivity như normalize columns/rows của Linear weights, hoặc sử dụng phép chiếu như paper Parseval network.
• Thêm noise vào autoencoder: một ý tưởng khá mới của tác giả là sử dụng một autoencoder ở trước một mô hình bất kỳ, và train nó độc lớp với dataset. Từ đó chúng ta có thể coi sensitivity của hàm này giống như của hàm identity (option 1).

    Cuối cùng, chúng ta chỉ cần cho nhiễu vào bằng Laplacian hoặc Gaussian mechanism, phụ thuộc vào yêu cầu của bài toán thôi

Ước lượng vùng an toàn tấn công

    Từ công thức trên thì phần này khá đơn giản: nếu thỏa mãn điều kiện ở trên thì prediction của model sẽ an toàn trong khoảng $\Vert\cdot\Vert_p\le L$ nếu như:

• Đảm bảo confidence của prediction:

    $$\mathbb{E}[A_k(x)] > e^{2\varepsilon}\max_{i\ne k}\mathbb{E}[A_i(x)] + (1+e^\varepsilon)\delta$$

• Nhiễu đủ lớn để thỏa mãn DP:
  • Với Laplace mechanism: $\sigma=\Delta_{p,1}L/\varepsilon, \delta=0$
  • Với Gaussian mechanism: $\sigma=\sqrt{2\ln(1.25/\delta)}\Delta_{p,2}L/\varepsilon, \varepsilon\le 1$

    Trong quá trình training, nếu chúng ta có threat model (ví dụ, tối đa thay đổi input là 8/255 thì mắt thường không nhận ra), chúng ta có thể tính $L$ đủ lớn cần thiết để sử dụng luôn trong quá trình sinh noise lúc training.

    Các giá trị expectation chúng ta có thể ước lượng bằng Monte Carlo methods. Confidence của đảm bảo an toàn trên sẽ phụ thuộc vào confidence của Monte Carlo estimate, và confidence sẽ tiến dần về 1 khi chúng ta tăng số sample được sử dụng trong estimate. Chúng ta có thể sử dụng bound trên để tính độ robustness của mô hình trên test set và có được một unbiased estimator cho độ an toàn của mô hình đối với một data (sạch) ngoài kia mà mô hình chưa thấy bao giờ.

Hết rồi, train và chạy thôi

    À, cẩn thận không được dùng Batch Normalization trong trường hợp bạn đặt noise layer đâu đó giữa mô hình nhé, vì batchnorm làm hỏng hết tất cả các ước lượng sensitivity đó

Random Self-Ensemble

    Được viết bởi Liu et. al từ UC Davis, Random Self-Ensemble (RSE) là một phương pháp thêm nhiễu vào mô hình khá là giống với PixelDP - tác giả có công nhận điều này và nói thêm rằng PixelDP chỉ được survey ra khi RSE sắp được nghiên cứu xong, và ý tưởng cơ bản của RSE khác hoàn toàn với PixelDP - Liu et. al tin rằng adversarial robustness nên được phân tích độc lập với DP, và mối tương quan với DP kia chỉ là một hiện tượng trùng hợp thú vị.

    Thiết kế của mô hình RSE khá đơn giản: thêm nhiễu vào đầu vào của mỗi layer, và train cùng với nhiễu. Điều đó tương ứng với việc ensemble các mô hình với các biases khác nhau, một ý tưởng khá giống với Dropout (ensemble các mô hình với các weight bị đục lỗ/zeroed out khác nhau) - từ đó suy ra cái tên RSE.

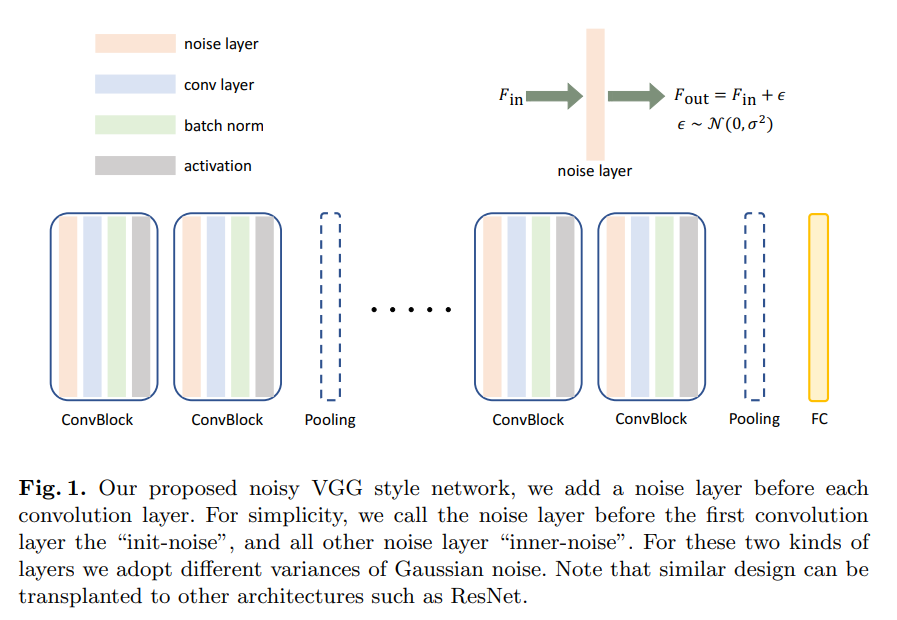
    Trong đó, có một vài chi tiết quan trọng cần lưu ý:

• Mô hình được train cùng với nhiễu trong input, và clean labels (ground truth)
• Nhiễu được đưa vào đầu vào của mô hình từ phân bố $\mathcal{N}(0,\sigma^2)$, và nhiễu đầu vào của các lớp ở giữa được draw từ cùng một phân bố $\mathcal{N}(0,\sigma'^2)$ khác với phân bố của nhiều đầu vào mô hình.
• Như đã đề cập ở trên, mô hình RSE chỉ có thêm 2 hyperparameters cho standard deviation của univariate distribution của nhiễu, và các giá trị này được grid search như bình thường để tìm ra giá trị tối ưu.
• Evaluation của mô hình sử dụng trung bình của nhiều lần inferences.

    Phần thú vị của paper này lại nằm ở phần toán Với các mô hình sử dụng log-likelihood loss, việc tối ưu hóa trọng số mô hình có thể được biểu diễn dưới dạng công thức như sau:

    $$w^* = \argmin_w\mathbb{E}_{(x_i, y_i)\in\mathcal{D}_\mathrm{train}}\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}\left[-\log f_\epsilon(w,x_i)[y_i]\right]$$

    Và trong quá trình evaluation, chúng ta lấy trung bình của nhiều lần inferences và chon class có logit lớn nhất:

    $$\hat{y}_i = \argmax\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}f_\sigma(w,x_i)$$

    Với một chút ✨handwavy math✨ thì chúng ta sẽ phân tích được phần trong $\argmin$ của vế bên phải phần tối ưu hóa trọng số như sau:

    $$\begin{aligned} & \mathbb{E}_{(x_i, y_i)\in\mathcal{D}_\mathrm{train}}\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}\left[-\log f_\epsilon(w,x_i)[y_i]\right]\\ \overset{(a)}{\approx}\;& \mathbb{E}_{(x_i, y_i)\in\mathcal{D}_\mathrm{data}}\left[-\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}\log f_\epsilon(w,x_i)[y_i]\right]\\ \overset{(b)}{\ge}\;& \mathbb{E}_{(x_i, y_i)\in\mathcal{D}_\mathrm{data}}\left[-\log\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}f_\epsilon(w,x_i)[y_i]\right]\\ \overset{(c)}{\ge}\;& \mathbb{E}_{(x_i, y_i)\in\mathcal{D}_\mathrm{data}}\left[-\log\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}f_\epsilon(w,x_i)[\hat{y}_i]\right]\\ \overset{(a)}{\approx}\;& \mathbb{E}_{(x_i, y_i)\in\mathcal{D}_\mathrm{test}}\left[-\log\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}f_\epsilon(w,x_i)[\hat{y}_i]\right]\\ \end{aligned}$$

    Nghĩa là, tối thiểu hóa hàm loss trên toàn bộ training set của chúng ta tương đương với việc tối thiểu hóa giới hạn trên của hàm loss của quá trình evaluation toàn bộ test set (sau khi tính trung bình nhiều lần inferences). Trong quá trình biến đổi trên, $(a)$ là do Law of Large Numbers, $(b)$ là theo bất đẳng thức Jensen, và $(c)$ là do cách chúng ta chọn kết quả inference $\hat{y}_i$. Thực ra chúng ta có thể bỏ bước cuối để chỉ lấy kết luận với data random ngoài kia thay vì chỉ trong test set.

    Ngoài ra, để ý rằng adversarial robustness tương ứng với (local) Lipschitz smoothness. Tác giả đã sử dụng Taylor's series expansion để chứng minh rằng sử dụng RSE tương ứng với Lipschitz regularization, khiến cho hàm loss khi sử dụng mô hình smooth xung quanh các data (khác với định nghĩa bình thường là classifier boundary smooth):

    $$\begin{aligned} &\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}l(f_\epsilon(w,x_i), y_i)\\ \overset{(a)}\approx\;&\mathbb{E}_{\epsilon\sim\mathcal{N}(0,\sigma^2)}\left[l(f_0(w,x_i),y_i) + \epsilon^\top\nabla_\epsilon l(f_0(w,x_i), y_i)+\frac{1}{2}\epsilon^\top\nabla_\epsilon^2l(f_0(w,x_i), y_i)\epsilon\right]\\ \overset{(b)}=\;& l(f_0(w,x_i), y_i) + \frac{\sigma^2}{2}\mathrm{Tr}(\nabla_\epsilon^2l(f_0(w,x_i), y_i)) \end{aligned}$$

    Trong đó, $(a)$ là từ Taylor expansion với $\epsilon$ rất bé do chúng ta chỉ inject một lượng nhỏ nhiễu, $(b)$ là do sau khi chúng ta tách từng số hạng và thay vào first/second moment của nhiễu (phần toán cụ thể để dành cho bạn đọc). Sử dụng trick convex relaxation và coi $l\circ f_0$ là hàm lồi, chúng ta có $\mathrm{Tr}(A)\ge\Vert A\Vert_2$ với $A$ positive definite. Từ đó chúng ta có

    $$\mathrm{Loss}(f_\epsilon, (x,y))\simeq\mathrm{Loss}(f_0, (x,y))+\frac{\sigma^2}{2}\Vert\nabla_\epsilon^2[l\circ f_0]\Vert_2$$

    trong đó giá trị bên trái được tối ưu khi chúng ta sample nhiễu nhiều lần trên data trong quá trình training, số hạng đầu trong vế bên phải chính là loss trên clean data, và số hạng thứ 2 tương ứng với độ smooth của gradient của hàm loss - khác với trong paper, tác giả nói là Lipschitz constant của hàm loss, nghĩa là độ smooth của hàm loss luôn. Về tác dụng của smooth gradient của hàm loss, và việc tối thiểu hóa các eigenvalue của ma trận Hessian (trong paper này là Laplacian chứ không phải Hessian, nhưng cũng tương tự), các bạn có thể tham khảo ở một paper khá hay này.

    ^{Nếu mình sai mong các cao nhân chỉ giáo, mình viết đoạn này vào 1h sáng và não mình tắt luôn rồi.}

Parametric Noise Injection

    Được viết bởi Rakin et. al từ UCF, Parametric Noise Injection (PNI) cải tiến thiết kế của RSE bằng cách thêm nhiễu mọi lúc mọi nơi. Chỗ nào có tensor, chỗ đó cho thêm nhiễu. Cụ thể, người dùng có thể chọn thêm nhiễu vào trong các tensor trọng số, hoặc thêm vào các đầu ra sau kích hoạt của các lớp của mô hình, hoặc cả 2. Điểm lợi là thêm nhiễu thêm vui (kết quả báo cáo cao hơn so với RSE), và điểm hại là tất cả lý thuyết đã viết của RSE bị ném ra cửa sổ - PNI thuần túy là một paper thông báo các kết quả thực nghiệm.

    Bởi vì như mình đã kể trên là paper này rất đơn giản nên mình sẽ chỉ tóm tắt configuration của paper thôi nhé:

• Noise được sample từ phân bố chuẩn với mean 0 và variance của signal tensor (weight hoặc post-activation tensor), sau đó scale với một trainable scalar/parameter alpha.

    $$\tilde{\mathbf{v}}=f_\mathrm{PNI}(\mathbf{v}) + \alpha\cdot\eta;\;\;\eta\sim\mathcal{N}(0,\mathrm{Var}(\mathbf{v}))$$

    Chú ý rằng với mỗi một tensor chỉ sample đúng 1 random variable, và chỉ có 1 trainable parameter để scale nhiễu.

• Cần sử dụng adversarial training để cho các noise scalar không bị về 0: nếu train bình thường thì mô hình sẽ học được rằng không có nhiễu là tốt nhất.
• Tính hàm loss trên cả clean data và adversarial data: loss tổng là một tổng có trọng số giữa 2 thành phần trên.

    $$\mathcal{L}'=w_c\cdot\mathcal{L}(g(\mathbf{x}; f_\mathrm{PNI}(\mathbf{\theta})), t)+w_a\cdot\mathcal{L}(g(\hat{\mathbf{x}}; f_\mathrm{PNI}(\mathbf{\theta})), t)$$

• Có chèn nhiễn vào trong quá trình evaluation, không lấy trung bình của nhiều lần inferences.

    Kết quả thì nói chung là tốt hơn RSE, và không bị tấn công bởi Expectation-over-Transformation; nghĩa là, việc thêm nhiễu ở đây không phải là gradient obfuscation.

    ^{Paper này content khá ít nên tóm tắt ngắn và không có ảnh minh họa nào trong paper mà đưa vào bài được cả.}

Learn2Perturb

    Được viết bởi Jeddi et. al từ University of Waterloo, Learn2Perturb là một phiên bản nữa cho một mô hình chèn nhiễu, với nhiều cải tiến khác nhau so với PNI.

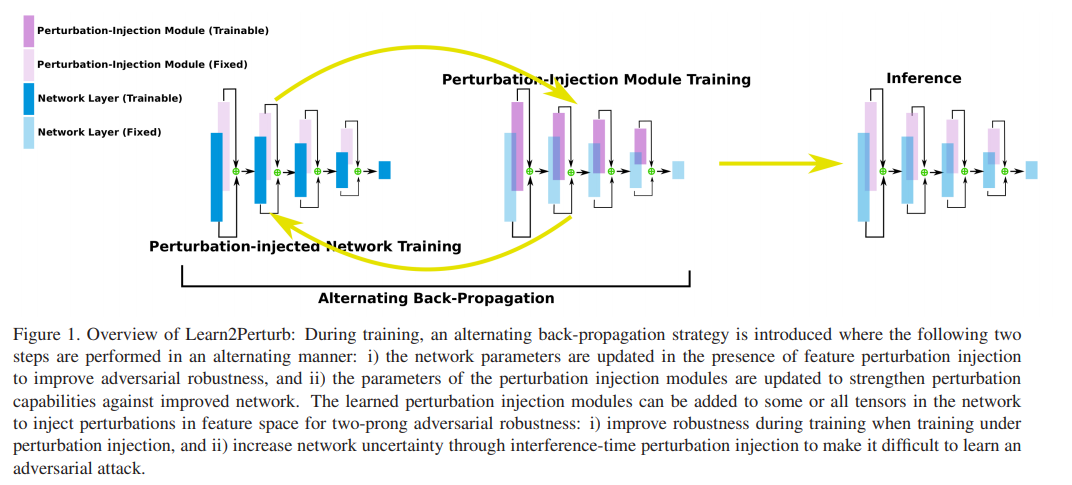
    Một bức tranh bằng ngàn câu chữ, các bạn hay nhìn vào ảnh ở trên để có thể hiểu được phương pháp này. Mỗi layer của mô hình (cụ thể là paper này thí nghiệm trên ResNet) là tổng của 2 phần $f_W(X) + Q(\theta)$, trong đó phần màu xanh là Dense/Linear/Convolutional layer $f_W(X)$ với trọng số là $W$ và data $X$ (sau activation), và phần màu tím hồng là nơi chèn nhiễu $Q(\theta)$. Nhiễu được chèn ở đây được lấy từ phân bố chuẩn xung quanh điểm 0: $Q(\theta)\sim\theta\cdot\mathcal{N}(0, \mathbf{I})$, với $\theta$ là cũng là trọng số có thể train được.¹ Tuy nhiên, khác với PNI thì Learn2Perturb không sử dụng adversarial training, vì:

• Train mô hình bằng adversarial training lâu hơn rất nhiều so với training bình thường
• Sử dụng phương pháp adversarial training thì kết quả của paper sẽ chỉ mang tính cải tiến không đáng kể (incremental).

    Thay vì sử dụng adversarial training để giữ độ lớn của nhiễu không xuống 0 trong quá trình training, Learn2Perturb sử dụng 2 (bộ) kỹ thuật: đầu tiên là alternating optimization (như trên hình), khi mô hình train tầm vài epoch với phần nhiễu $Q(\theta)$ bị đóng băng, rồi train vài epoch với phần mô hình $f_W(X)$ đóng băng, và cứ thế so le. Còn lại là một combo của 3 kỹ thuật nhỏ hơn:

• Regularization: như các bài toán tối ưu nhiều hơn 1 mục tiêu, Learn2Perturb đưa thêm một regularization term $g(\theta)$ tỉ lệ nghịch với $\theta$ để giữ cho độ lớn của nhiễu cao:

    $$\argmin_{W,\theta}(\mathcal{L}(P(X;W,\theta), T) + \gamma\cdot g(\theta))$$

    trong đó $\gamma$ là regularization coefficient như bình thường.

• Harmonic annealing: hàm regularization được định nghĩa là

    $$g(\theta)=-\frac{\theta^{1/2}}{\tau}$$

    Do nếu chỉ sử dụng công thức trên thì khi tối ưu objective, trọng số có thể tăng lên không giới hạn. Vì thế, trong hàm $g$ sẽ phải giảm dần theo thời gian, nhờ giá trị $\tau$ là kết quả của dãy harmonic theo số epoch hiện tại $k$:

    $$\tau(k)=\sum_{i=1}^k\frac{1}{i}$$

• Hard minimum-clipping ²: Nếu giá trị của noise scalar nhỏ quá thì chúng ta điều chỉnh nó lại về mức tối thiểu cho phép – tương tự với khi chúng ta clip/project adversarial example trong khoảng cho phép. Công thức cụ thể sẽ phụ thuộc vào norm được sử dụng, nhưng trong trường hợp đơn giản nhất là 1D thì công thức sẽ là:

    $$\theta\leftarrow\max(\theta, \theta_\mathrm{min})$$

    Sau khi train thì mô hình được evaluate có kèm nhiễu (như hình trên). Tương tự như các bài báo khác, Learn2Perturb (được các tác giả claim rằng) không xảy ra hiện tượng gradient obfuscation, và kết quả của Learrn2Perturb trên các thí nghiệm tương tự đều tốt hơn các paper đi trước.

    ¹ Trong paper tác giả ghi là $Q(\theta)\sim\theta\cdot\mathcal{N}(0, 1)$, nhưng trong code của họ sample sử dụng normal_(); ngoài ra họ cũng claim là $P(X; W,\theta)\sim\mathcal{N}(f(X,W), \theta)$, trong khi đúng ra covariance phải là $\theta^2$.

    ² Tên phương pháp là mình tự bịa hết nhé.

Attack-Agnostic Stochastic Neural Network

    Được viết bởi Eustratiadis et. al từ University of Edinburgh, A²SNN (trước gọi là WCA-Net ³) là một phiên bản nữa cho một mô hình chèn nhiễu, nhưng lần này là với anisotropic noise – nghĩa là, lần này nhiễu sẽ được lấy ra (draw) từ normal distribution nhưng với ma trận covariance là symmetric positive semi-definite thôi thay vì là diagonal như các bài trước. Cụ thể, phân bố của nhiễu trong thiết kế mạng này là $\mathcal{N}(0, \mathbf{\Sigma})$, trong đó $\mathbf{\Sigma}=\mathbf{L}\cdot\mathbf{L}^\top$, và $\mathbf{L}$ là một lower-triangular matrix. Từ đó, chúng ta có thể sample một cách hiệu quả từ phân bố trên như sau:

    $$z\sim\mathcal{N}(0, \mathbf{\Sigma})\equiv\mathbf{L}\cdot\mathcal{N}(0, \mathbf{I})$$

    Tuy nhiên, khác với các thiết kế trên thì mô hình này lại chỉ thêm nhiễu vào đầu vào của layer classification cuối cùng, thay vì thêm tứ tung như PNI/L2P, hay vào ngay đầu như RSE.

    Tương tự với L2P, A²SNN không sử dụng adversarial training, mà sử dụng các loại regularization để giữ cho nhiễu lớn hơn 0. Cụ thể, hàm mất mát được sử dụng ngoài cross-entropy cho các mô hình phân lớp, có 2 phần regularization khác:

    $$\mathcal{L}=\mathcal{L}_C-\lambda_1\mathcal{L}_\mathrm{ME}-\lambda_2\mathcal{L}_\mathrm{WCA}$$

• Max-Entropy Regularization ⁴: Tương tự với Learn2Perturb, A²SNN sử dụng regularization với $\mathbf{L}$ với mục đích là để tối đa hóa entropy của phân bố nhiễu:

    $$\mathcal{L}_\mathrm{ME}=\frac{1}{2}\ln\det(2\pi e\Sigma)$$

• Weight-Covariance Alignment: dựa vào chứng minh toán học trong paper mà các tác giả đưa ra được kết luận rằng, mô hình sẽ hoạt động tốt nhất khi covariance của nhiễu khớp với các vector đại diện các class đầu ra (được biểu diễn bởi weight matrix tại layer cuối cùng). Từ đó, tác giả đưa ra được công thức:

    $$\mathcal{L}_\mathrm{WCA}=\sum_{i=1}^C\ln(w_i^\top\Sigma w_i)$$

    trong đó $C$ là số class đầu ra, và $w_i$ là các vector hàng trong weight matrix của lớp classification (Dense/Linear) cuối mạng.

    Tóm tắt về giải thích của công thức trên là như sau:

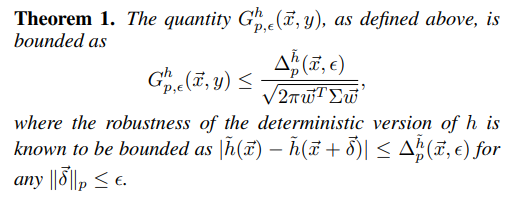
    với $G^h_{p,\epsilon}(x, y)=\max_{\delta:\Vert\delta\Vert_p\le\epsilon}\mathbb{P}[yh(x+\delta)\le 0] -\mathbb{P}[yh(x)\le 0]$ là một giá trị đo đạc khả năng bị tấn công của mô hình chèn nhiễu, và $\Delta^h_{p,\epsilon}$ cũng là giá trị đó nhưng cho một mô hình không có nhiễu. Vì vậy, nếu chúng ta tối đa hóa mẫu số của chặn trên của $G$, thì chúng ta đang gián tiếp tối thiểu hóa $G$. Phần chứng minh thì nếu bạn muốn biết mình thực sự nghĩ bạn nên đọc paper, vì nó rất nhiều các loại ký tự mọi nơi, và mình không thể phân tích rõ ràng hơn phần chứng minh trong paper được đâu.

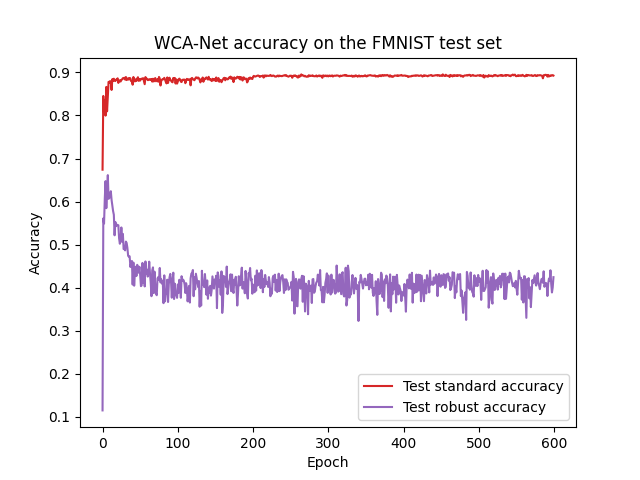
    Tương tự với Learn2Perturb thì sau khi train thì mô hình được evaluate có kèm nhiễu; và tương tự như các bài báo khác, A²SNN (được các tác giả claim rằng) không xảy ra hiện tượng gradient obfuscation, và kết quả trên các thí nghiệm tương tự đều tốt hơn các paper đi trước. Tuy nhiên, có một vài vấn đề xuất hiện trong quá trình reproduce paper này: link repo trên phiên bản mới (v1) của bài này là dead link không truy cập được, còn link trên phiên bản gốc của paper vẫn sống (và last updated là tháng 5 năm nay!) nên mình đã làm thí nghiệm trên repo này. Mình không train lại trên ResNet vì máy quá yếu, mà đã sử dụng setup WCA của họ (như trong paper) với dataset Fashion-MNIST trên LeNet++, và kết quả khá là toang. Cụ thể là có 2 vấn đề:

• Parameter lower-triangular matrix $\mathbf{L}$ mà họ dùng để scale nhiễu từ $\mathcal{N}(0, \mathbf{I})$ sang $\mathcal{N}(0, \mathbf{L}\cdot\mathbf{L}^\top)$ không có yêu cầu gì cụ thể. Tuy nhiên họ sử dụng class MultivariateNormal trong PyTorch, và yêu cầu của parameter scale_tril là một ma trận vuông lower-triangular với các giá trị trên đường chéo dương (nếu bạn cung cấp variance matrix thay vì scaling matrix thì class cũng chạy Cholesky decomposition để sinh ra scaling matrix thôi). Vì vậy, trong code train của mình đã phải tạo một hàm handle vấn đề này tương tự với ReLU:

    $$\mathbf{L}\leftarrow\max(\mathbf{L},10^{-8})$$

• A²SNN đượctrain với 600 (!) epochs, và kết quả robust accuracy (đo bằng AutoAttack, code ở đây) tốt nhất đạt được khá sớm và thấp, sau đó xuống dần không phanh, như đã thấy trong hiện tượng Robust overfitting. Tuy nhiên clean test accuracy vẫn tăng mà không có hiện tượng overfitting, chứng tỏ thiết kế mô hình chèn nhiễu của họ ít nhất cũng đã thành công trong phương pháp này. Evaluation plot do mình chạy được show ra dưới đây:

    ³ Bài này mình sử dụng code từ phiên bản cũ của paper này, nên nếu có gì đã thay đổi mong mọi người chỉ ra giúp.

    ⁴ Tên phương pháp lần này là từ paper chứ không phải tự bịa gì đâu nhé.

Kết bài

    Hết thật rồi Bài này quá dài và quá nhiều paper survey, lại còn là chủ đề ngách nên mình không nghĩ sẽ có ai đọc hết đâu. Nếu bạn đã đọc đến đây thì mình cảm ơn rất nhiều đã quan tâm theo dõi content của mình. Giờ thì xin chào và hẹn gặp lai!