Ngày nay, Image Segmentation đã trở thành 1 lĩnh vực nghiên cứu tích cực, vì nó giúp ích rất nhiều trong ứng dụng thực tiễn, từ tự động phát hiện bệnh cho đến ứng dụng xe tự hành.

    Trong 5 năm qua, có rất nhiều bài báo nói về các loss function, mỗi loss function lại phù hợp với 1 trường hợp bài toán riêng, ví dụ như biased data, sparse segmentation, ... Vậy trong bài viết này, chúng ta cùng tổng kết lại một số loss function được biết đến và được dùng rộng rãi trong bài toán Image Segmentation, cũng như việc liệt kê ra các trường hợp mà chúng giúp cho việc hội tụ nhanh hơn và tốt hơn của mô hình học sâu.

    Xa hơn 1 chút, chúng ta cùng tìm hiểu về log-cosh dice loss và so sánh hiệu năng của nó với các loss function phổ biến khác, dựa trên bộ dữ liệu mã nguồn mở NBFS skull-segmentation.

Giới thiệu

    Image segmentation được định nghĩa giống như bài toán classification cho từng pixel trên ảnh. 1 ảnh có rất nhiều pixel, chúng được nhóm cùng nhau để tạo ra các thành phần khác nhau trong trong ảnh. 1 phương thức của việc phân loại đó được gọi là Semantic segmentation.

    Vào năm 2012, các nhà nghiên cứu đã thử nghiệm hàm loss function riêng biệt trên nhiều vùng khác nhau để cải thiện kết quả cho bộ dữ liệu của họ. Chúng ta cùng điểm qua 15 hàm loss function 'cốt cán' nhất trong bài toán semantic segmentation. Về cơ bản chúng được chia làm 4 loại chính:

• Distributed-based: Dựa trên phân phối
• Region-based: Dựa trên miền
• Boundary-based: Dựa trên biên
• Compounded-based: Dựa trên kết hợp

    Qua đó, chúng ta cũng bàn về điều kiện tiên quyết để 1 hàm loss function hữu dụng trong 1 tình huống bài toán nhất định.

    Ngoài ra, tác giả còn đề xuất 1 hàm loss function mới có tên Log-cosh cho bài toán Semantic segmentation. Để chỉ ra tính hiệu quả của nó, chúng ta cùng so sánh nó với tất cả các loss function khác trong bộ dữ liệu NBFS Skull-stripping.

    Dưới đây là bảng liệt kê các loss function và thể loại của chúng:

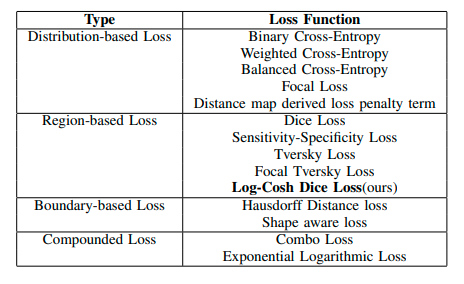
15 Loss Function

    Trong bài báo này, chúng ta tập trung và Sematic Segmentation thay vì Instance Segmentation, chính vì thế số nhãn bị bạn chế là 2 nhãn.

Binary Cross-Entropy

    Cross-Entropy được định nghĩa là 1 thước đo sự khác nhau giữa 2 phân phối xác suất của 1 biến ngẫu nhiên. Nó được sử dụng rộng rãi cho bài toán phân loại đối tượng. Cũng giống như segmentation, là phân loại trên các pixel.

    $$L_{Binary-CE}(y, \hat y) = -(y log(\hat y) + (1 - y)log(1 - \hat y))$$

Weighted Binary Cross-Entropy

    WCE là 1 biến thể của Binary Cross-Entropy. Được sử dụng rộng rãi trong các bộ dữ liệu bị 'lệch'. Hàm loss này chỉ quan tâm đến các mẫu positives, nên nó chỉ đánh trọng số cho mẫu positives.

    $$L_{Weighted-BCE}(y, \hat y) = -(\beta *y log(\hat y) + (1 - y)log(1 - \hat y))$$

    $\beta$ được dùng để điều chỉnh số lượng false negatives và false positives. Nếu chúng ta muốn giảm số lượng false negatives thì $\beta > 1$, để giảm số lượng false positives thì $\beta < 1$.

Balanced Cross-Entropy

    BCE lại là 1 biến thể của W-BCE, chỉ khác là BCE quan tâm tới cả 2 mẫu negatives và positives, nên cả 2 đều được đánh trọng số.

    $$L_{Balanced-CE}(y, \hat y) = -(\beta *y log(\hat y) + (1-\beta) * (1 - y)log(1 - \hat y))$$

    Ở đây, $\beta = 1 - \frac y {H * W}$, trong đó: $H * W$ là tổng số pixel trong ảnh.

Focal Loss

    Focal Loss (FL) cũng được xem là 1 biến thể của Balanced-CE.

    Từ công thức của Cross-Entropy, ta có thể tóm gọm lại như sau:

    $$CE = \begin{cases} -log(p_i), &\text{if } y = 1 \\ -log(1-p_i), &\text{otherwise} \end{cases}$$

    Trong đó: $p_i$ là tần suất xuất hiện của nhãn $i$

    Viết gọn hơn, chúng ta được như sau:

    $$CE = -log(p_i)$$

    và:

    $$\text{Balanced-CE} = -\beta log(p_i)$$

    Công thức của Focal Loss như sau: $FL = -\beta (1 - p_i)^\gamma log(p_i)$

    Mục đích thêm nhân tử đó:

• Hạn chế sự ảnh hưởng của các mẫu dễ dự báo lên loss function, các mẫu dễ dự báo thường có $p_i$ cao hơn, việc thêm $(1 - p_i)^\gamma$ sẽ hạn chế ảnh hưởng đó
• Phạt nặng vào các mẫu khó dự báo, thường $p_i$ của các mẫu khó dự báo sẽ thấp hơn.

Dice Loss

    Hằng số Dice được sử dụng rộng rãi để đo độ giống nhau của 2 ảnh. Vào cuối năm 2016, nó được phát triển thành 1 loss function gọi là Dice Loss:

    $$DL(y, \hat y)=\frac{y+\hat{y} - 2 y \hat{y}} {y + \hat{y} + \alpha}$$

    Ở đây, $\alpha$ là số rất nhỏ để đảm bảo mẫu số của biểu thức luôn khác 0

Tversky Loss

    Độ đo Tversky cũng được gọi là 1 biến thể của độ đo Dice

    $$TI(y, \hat y)=\frac {y \hat y} {y \hat{y} + \beta (1-y) \hat{y} + (1 - \beta)y (1- \hat y)}$$

    Khi $\beta = 1 / 2$ thì công thức trở thành độ đo Dice

    Cũng từ đó sẽ có Tversky Loss:

    $$TL(y, \hat y)=\frac {\beta(1-y)\hat{y} + (1-\beta)y(1-\hat y)}{y\hat{y} + \beta(1-y)\hat{y} + (1-\beta)y(1-\hat y) + \alpha}$$

Focal Tversky Loss

    Cũng giống như Focal Loss, Focal Tversky Loss cũng tập trung vào việc giảm ảnh hưởng của các mẫu dễ dự báo, phạt nặng vào các mẫu khó dự báo.

    $$FTL = \displaystyle\sum_{c} {(1 - TI_c)^\gamma}$$

Sensitivity Specificity Loss

    Sensitivity Specificiry Loss được định nghĩa như sau:

    $$SSL = w * sensitivity + (1-w) * specificity$$

    Trong đó:

    $$sensitivity = \frac {TP} {TP +FN}$$

    $$specificity = \frac {TN} {TN +FP}$$

Shape-aware Loss

    Nhìn chung, hầu hết các hàm loss đều làm việc ở cấp độ là các pixel. Tuy nhiên, Shape-aware loss lại tính điểm trung bình để đường cong Euclid ở giữa các điểm xung quanh đường cong được dự đoán, và sử dụng nó như 1 hệ số trong Cross-Entropy loss.

    $$E_i = D(\hat C, C_{GT})$$

    $$L_\text{shape-aware}=-\displaystyle\sum_i {CE(y, \hat y) - \displaystyle\sum_i E_i CE(y, \hat y)}$$

    $E_i$ được coi là 1 mặt nạ mạng được học tương tự như các training shape

Combo loss

    Combo loss được định nghĩa giống như 1 trung bình trọng số của Dice loss và là 1 biến thể từ Cross entropy. Nó cố gắng tận dụng sự linh hoạt của Dice loss và cùng lúc sử dụng cả Cross Entropy để làm mượt đường cong biến thiên.

    $$L_\text{m-bce}=-\frac{1}{N} \displaystyle\sum_i \beta(y-log(\hat y)) + (1-\beta)(1-y)log(1-\hat y)$$

    $$CL(y, \hat y)=\alpha L_\text{m-bce} - (1-\alpha)DL(y, \hat y)$$

    Ở đây DL chính là Dice loss

Exponential Logarithmic Loss

    ELL tập trung vào các cấu trúc được dự đoán kém chính xác hơn, sử dụng kết hợp giữa Dice loss và Cross Entropy.

    Tác giả đề xuất 1 chuyển đổi có logarit và mũ cho cả Dice loss và Cross Entropy để kết hợp lợi ích của cả 2.

    $$L_\text{Exp}=w_{Dice} L_{Dice} + w_{cross} L_{cross}$$

    ở đây: $L_{Dice} = E(-ln(DC)^{\gamma_{Dice}})$

    $$L_{cross} = E(w_l (-ln(p_l))^{\gamma_{cross}})$$

    Chúng ta có thể sử dụng $\gamma_{cross} = \gamma_{Dice}$

Distance map derived loss

    Distance map được định nghĩa là khoảng cách giữa ground truth và predicted map. Có 2 cách để kết hợp các bản đồ khoảng cách: Tạo 1 kiến trúc mạng neural mà có 1 đầu tái cấu trúc với segmentation, hoặc đưa nó trở thành 1 loss function.

    Caliva đã sử dụng bản đồ khoảng cách lấy được từ mặt nạ ground truth và tạo 1 mức phạt tùy chỉnh dựa trên loss function. Sử dụng cách tiếp cận này, có 1 cách dễ dàng để làm cho mạng tập trung vào các miền boundary khó segment.

    Hàm loss được định nghĩa như sau:

    $$DMDL = \frac{1}{N}\displaystyle\sum_{i=1}^{N} (1+\phi)(\odot)L_{CE}(y, \hat y)$$

    Ở đây $\phi$ được tạo từ các distance maps. Hằng số $1$ được thêm vào để tránh vấn đề tiêu biến gradient trong các kiến trúc mạng U-net và V-net.

Hausdorff Distance Loss

    HDL là 1 thước đo được sử dụng trong các cách tiếp cận segmentation để theo dõi hiệu năng của mô hình. Nó được định nghĩa như sau:

    $$d(X, Y)=max_{x\in X}min_{y \in Y} \parallel x - y \parallel_2$$

    Mục tiêu của bất kỳ mô hình segmentation nào đó là tối đa hoá khoảng cách Hausdorff, nhưng vì tính chất của nó không phải hàm lồi, nên nó không được sử dụng rộng rãi như 1 loss function.

    Karimi đã đề xuất ra 3 biến thể của độ đo Hausdorff dựa trên các loss function, gồm có:

• Tối đa hóa các lỗi Hausdorff loss
• Tối thiểu hóa các lỗi Hausdorff loss thu được bằng việc đặt 1 kiến trúc hình tròn bán kính $r$
• Lấy đối đa các kernel tích chập được đặt trên đầu các pixel bị segment sai.

    Dưới đây là khoảng cách Hausdorff giữa các điểm của bộ dữ liệu X và Y

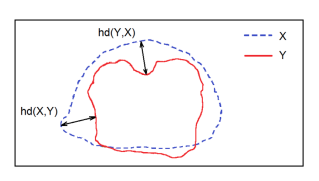
Correlation Maximized Structural Similarity

    Có rất nhiều hàm loss trong sematic segmentation tập trung vào lỗi phân loại các pixel trong khi lại không coi trọng thông tin cấu trúc của pixel đó. Có một số hàm loss đã cố gắng sử dụng thêm thông tin các kiến trúc có trước như CRF, GAN, ... Ở trong hàm loss này, tác giả đã giới thiệu Structural Similarity Loss (SSL) để đạt được sự tương quan tuyến tính tích cực cao giữa ground truth maps và predicted maps. Nó chia làm 3 bước:

• Structure Comparison
• Xác định hệ số Cross Entropy
• Định nghĩa hàm loss trên các mini-batch

    Trong bước Structure Comparison, tác giả định nghĩa 1 biến $e$ để đo sự tương đồng tuyến tính giữa ground truth và prediction:

    $$e = \mid \frac{y - \mu_y + C_4}{\sigma_y + C_4} - \frac{\hat y - \mu_{\hat y} + C_4}{\mu_{\hat y} + C_4} \mid$$

    Ở đây:

• $C_4$ là hệ số ổn định, thông thường theo kinh nghiệm thì bằng $0.01$
• $\mu_y$ và $\sigma_y$ lần lượt là giá trị trung bình cục bộ và độ lệch chuẩn của ground truth $y$.

    Sau khi tính được độ tương quan $e$. Tác giả sử dụng nó như 1 hệ số trong Cross Entropy, được định nghĩa như sau:

    $$f_{n, c}=1 * e_{n, c} > \beta e_{max}$$

    Sử dụng hệ số trên trong hàm tính $CMSSL$ như sau:

    $$CMSSL(y_{n, c}, \hat {y}_{n, c})=e{n, c} f{n, c} L_{CE}(y_{n, c} \hat {y}_{n, c})$$

    Và hàm loss được định nghĩa cho mini-batch như sau:

    $$CMSSL=\frac 1 {M} \displaystyle\sum_{n=1}^N \displaystyle\sum_{c=1}^C CMSSL(y_{n, c}, \hat y_{n, c})$$

    Trong đó: $M = \displaystyle\sum_{n=1}^N \displaystyle\sum_{c=1}^C f_{n, c}$. Sử dụng công thức bên trên, hàm loss sẽ tự động bỏ qua những pixel không thể hiện được độ tương quan trong cấu trúc.

Log-Cosh Dice Loss

    Độ đo Dice chúng ta đã nói phía trên tuy được sử dụng rộng rãi, nhưng nó không phải là một hàm lồi, nên nó có thể sai sót trong việc đạt được kết quả tối ưu.

    Lovsz-Softmax loss hướng tới việc giải quyết vấn đề hàm không lồi bằng cách thêm công cụ Lovsz để làm mượt. Cách tiếp cận Log Cosh được sử dụng rộng rãi trong hồi quy dựa trên việc làm mượt đường cong

    Hàm Cosh là giá trị trung bình của $e^x$ và $e^{-x}$

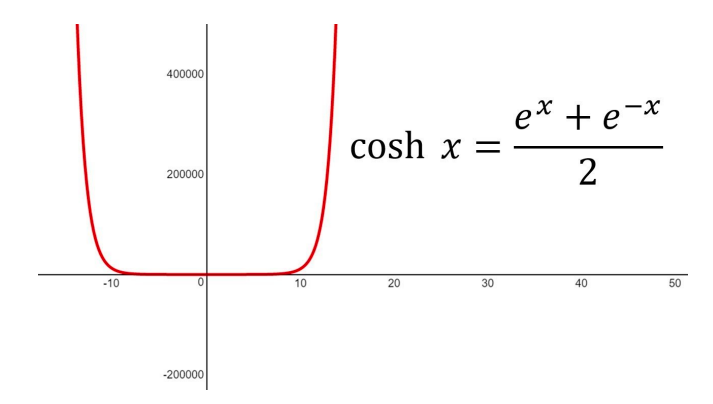
    Hàm $tanh(x)$ là liên tục và hữu hạn trong khoảng $[-1, 1]$

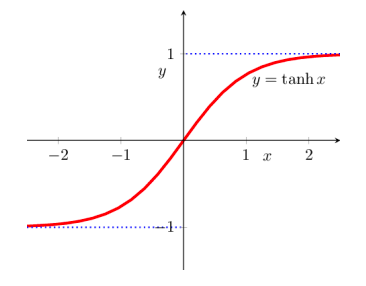
    Các hàm hypebol được sử dụng rộng rãi trong deep learning trong điều kiện các lớp phi tuyến như tanh, relu, ... Chúng dễ dàng được theo dõi và phân biệt 1 cách rõ ràng.

    Hàm $Cosh(x)$ được định nghĩa như sau

    $$cosh(x)=\frac{e^x + e^{-x}}{2}$$

    và đạo hàm của nó:

    $$cosh'(x)=\frac{e^x + e^{-x}}{2}=sinh(x)$$

    Nhưng khoảng giá trị của hàm $cosh(x)$ có thể tiến ra vô cùng, nên tác giả đã để nó vào hàm $log$. Từ đó, hàm log-cosh ra đời:

    $$L(x)=log(cosh(x))$$

    Sau khi dùng kỹ thuật change rule, ta có:

    $$L'(x)=\frac{sinh(x)}{cosh(x)}=tanh(x)$$

    Đây là 1 hàm liên tục và hữu hạn trong khoảng $[-1, 1]$

Các tình huống sử dụng các loss function

    Tác giả cũng đề xuất 1 hàm loss có tên là Log-Cosh Dice Loss function, nó dễ dàng theo dõi và đóng gói các tính năng của hệ số Dice, được định nghĩa như sau:

    $$L_{lc-dce}=log(cosh(DiceLoss))$$

Kinh nghiệm

    Theo như kinh nghiệm, tác giả đã triển khai kiến trúc mô hình Unet 2D đơn giản với 10 layer tích chập encoder đơn giản và 8 layer giải chập decoder, với bộ dữ liệu NBFS Skull-Stripping. Bộ dữ liệu gồm các ảnh về 125 hộp sọ, mỗi ảnh chứa 120 lát cắt. Huấn luyện với batch_size = 32, tối ưu adam, learning_rate = 0.001 và giảm xuống $10^{-8}$. Tác giả chia bộ dữ liệu thành training, validation và test tương ứng là 6-2-2.

    Tác giả triển khai với 9 hàm loss, do các hàm còn lại hoặc đã được kế thừa trong 9 hàm loss nói trên, hoặc không phù hợp với bộ dữ liệu NBFS. Sau khi huấn luyện, tác giả đã đánh giá chúng như sau:

    So sánh các hàm loss trên các độ đo Dice, Sensitivity và Specificity trên Skull Segmentation

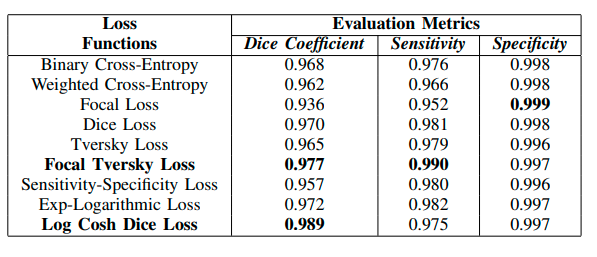
    với công thức trên các độ đo như sau:

    $$DC=\frac{2TP}{2TP + FP + FN}$$

    $$Sensitivity = \frac {TP}{TP + FN}$$

    $$Specificity = \frac {TN}{TN + FP}$$

Kết luận

    Việc chọn hàm loss là 1 tác vụ thiết yếu để xác định hiệu suất mô hình. Đối với các mục tiêu phức tạp như segmentation, chúng ta không thể khái quát hết trong 1 hàm loss chung chung được. Phần lớn thời gian sẽ phụ thuộc vào tính chất của bộ dữ liệu huấn luyện, như phân phối, độ lệch, đường biên.

    Không thể đề cập đến 1 loss function nào là tốt nhất, tuy nhiên chúng ta có thể nói rằng trong trường hợp dữ liệu mất cân bằng thì hàm loss nào hoạt động là tốt hơn.

    Trong bài báo này, tác giả đã tổng kết 14 hàm loss cho semantic segmentation và đề xuất 1 biến thể được lấy cảm hứng từ Dice loss function cho việc tối ưu được chính xác và tốt hơn. Trong tương lai, tác giả sẽ sử dụng nó làm cơ sở triển khai cho các thử nghiệm segmentation khác.

Tham khảo

    https://arxiv.org/pdf/2006.14822.pdf

    https://www.kaggle.com/bigironsphere/loss-function-library-keras-pytorch

    https://www.machinecurve.com/index.php/2019/10/23/how-to-use-logcosh-with-keras/