Lời mở đầu

    Chào các bạn, hôm nay tuy không rảnh lắm, nhưng mình vẫn thử dịch và viết một bài về Time Series data (dữ liệu theo thời gian). Bài viết này dựa trên ý hiểu của mình khi đọc bài gốc, có gì sai sót mong các bạn bỏ qua.

Định nghĩa

    Time series data là gì ? Để trả lời câu hỏi này, tôi sẽ đặt ra 3 tình huống:

1. Bạn làm quản lý ở một nhà hàng pizza, bạn thấy mỗi thứ 7 giá đơn hàng tăng lên một chút, bạn muốn biết việc bán ra của mình có theo một quy luật đặc biệt nào không.
2. Công ty của bạn bán một sản phẩm và bạn được giao nhiệm vụ dự đoán lượng mua, dự báo số nguyên liệu cần cho sản phẩm này.
3. Bạn là người duy trì hệ thống dữ liệu tập trung. Bạn muốn phát hiện ra những vấn đề xảy ra trong tiến trình của hệ thống như việc sử dụng CPU bất bình thường dẫn đến máy chủ sập. Vì vậy bạn phải theo dõi giá trị sử dụng CPU theo thời gian.

    Như các bạn thấy trong các ví dụ trên, tôi đã và đang làm việc với dữ liệu theo thời gian, từ đơn hàng cho đến dự đoán của sản phẩm, ... Thể hiện rõ nhất ở đây là biểu đồ chứng khoán.

    Trong xã hội hiện đại, khi lượng thông tin càng ngày càng tăng, việc phân tích dữ liệu time series trở nên cực kỳ quan trọng, nhưng cho dù có nhiều thuật toán hay mô hình trí tuệ nhân tạo sinh ra, việc dự đoán tương lai vẫn thất bại do sự thiếu ổn định trong chuỗi thời gian.

Một vài thuật ngữ trong Time Series

    Trend: xu hướng của dữ liệu (tăng hoặc giảm). Điều này có thể phát hiện thông qua độ dốc của dữ liệu trên biểu đồ.

    Seasonality: dữ liệu bị ảnh hưởng theo thước đo thời gian như: giờ, tuần, tháng, năm, ... Trong trường hợp, này dữ liệu có chu kỳ lặp đi lặp lại theo thước đo thời gian kể trên với một tần suất cố định.

    Cyclicity: một chu kỳ xảy ra khi dữ liệu tăng và giảm không theo một tần suất cố định. Dễ thấy nhất ở đây là trong lĩnh vực kinh tế.

    Residuals: dữ liệu time series có thể chia thành 2 loại: giá trị dự báo tại thời điểm t và phần thặng dư tại thời điểm t

    Value of series at time t = Predicted value at time t + Residual at time t

    Một số ví dụ:

• Chuỗi theo xu hướng tăng:

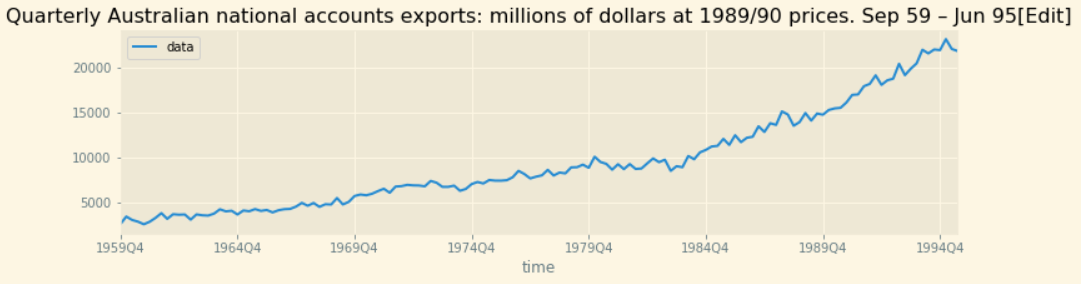
• Chuỗi theo chu kỳ với tần suất cố định:

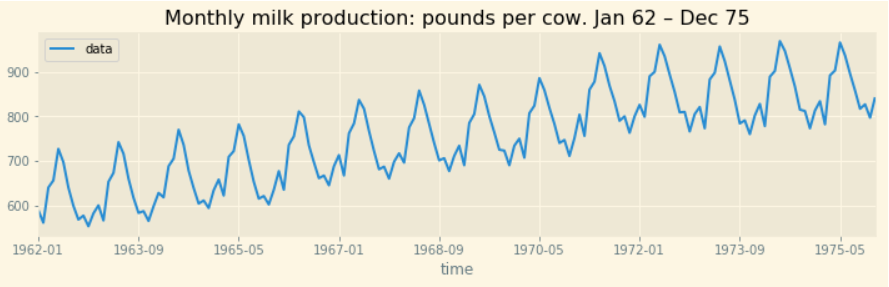
• Chuỗi theo chu kỳ với tần suất không cố định:

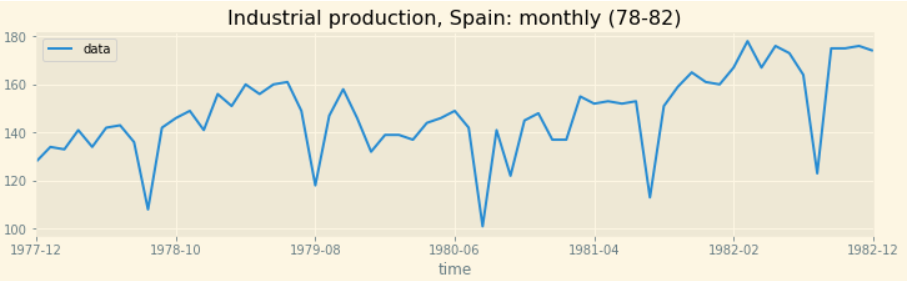
• Chuỗi chả theo thể loại gì:

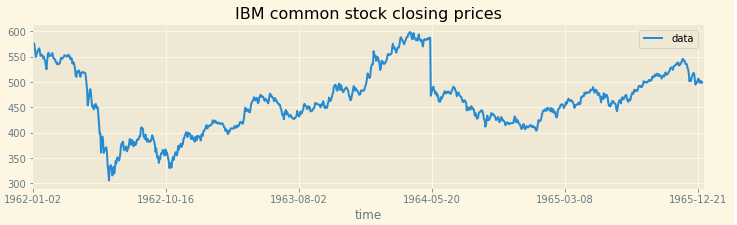
    Một chuỗi cũng có thể là tổ hợp của nhiều loại kể trên.

Tính ổn định của chuỗi

    Đơn giản hiểu là một chuỗi lặp đi lặp lại theo một chu kỳ, giá trị không tăng theo thời gian. Dự đoán chuỗi có tính ổn định rất dễ do có các đặc tính như: mean, variance, autocorrelation, ...

Biến đổi về chuỗi ổn định

    Đại đa số trường hợp chúng ta bắt gặp các chuỗi bất ổn định, vì vậy cần phải loại bỏ những yếu tố gây bất ổn định.

• De-trending (thủ tiêu xu hướng): như tên gọi, loại bỏ các khu vực mang yếu tố xu hướng trong chuỗi. Việc loại bỏ có nhiều cách, phụ thuộc vào bản chất của dữ liệu: index hay non-index.
• Differencing: seasonal hoặc cyclical có thể được loại bỏ bằng cách lấy giá trị quan sát tại thời điểm t trừ giá trị quan sát tại thời điểm t-1.
• Logging: nôm na là khi xu hướng không dựa trên chỉ số giá cả (trong trường hợp không phải chuỗi tiền tệ) , logging sẽ biến chuỗi thành một chuỗi tuyến tính (log(exp(x)).

Pratice code

Kiểm tra tính ổn định của chuỗi

Visualize

    Cách đơn giản nhất là quan sát chuỗi bằng mắt thường. Nếu bạn là dân code ngôn ngữ python-er như mình có thể dùng thư viện matplotlib để vẽ dữ liệu thành biểu đồ.

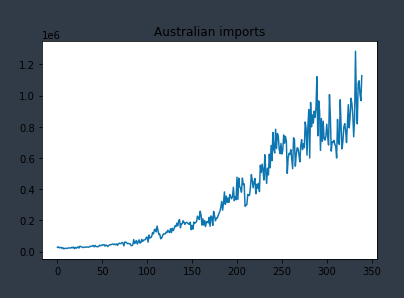
    Ở đây tôi dùng dữ liệu xuất nhập khẩu Úc-Nhật.

csv_path = "/home/pham.minh.hoang/Pictures/monthly-australian-imports-from-.csv"

data_imports = pd.read_csv(csv_path)[:-1:]
data = data_imports.drop(['Month'], 1)
data.values.reshape(-1,1)

plt.plot(data)
plt.title('Australian imports')
plt.show()

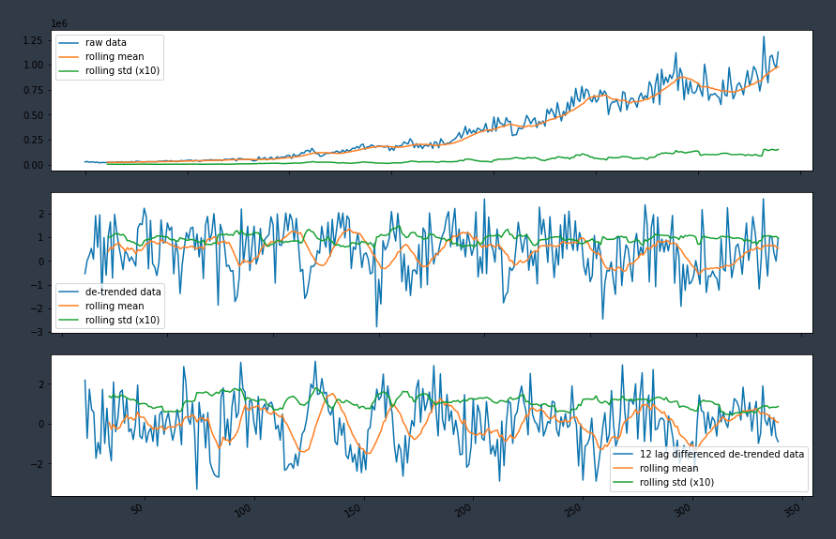
data_detrend = (data - data.rolling(window=12).mean()) / data.rolling(window=12).std()
data_season = data_detrend - data_detrend.shift(12)

fig, ax = plt.subplots(3,figsize=(12, 9))
ax[0].plot(data.index, data, label='raw data')
ax[0].plot(data.rolling(window=12).mean(), label="rolling mean");
ax[0].plot(data.rolling(window=12).std(), label="rolling std (x10)");
ax[0].legend()

ax[1].plot(data.index, data_detrend, label="de-trended data")
ax[1].plot(data_detrend.rolling(window=12).mean(), label="rolling mean");
ax[1].plot(data_detrend.rolling(window=12).std(), label="rolling std (x10)");
ax[1].legend()

ax[2].plot(data.index, data_season, label="12 lag differenced de-trended data")
ax[2].plot(data_season.rolling(window=12).mean(), label="rolling mean");
ax[2].plot(data_season.rolling(window=12).std(), label="rolling std (x10)");
ax[2].legend()

plt.tight_layout()
fig.autofmt_xdate()

Adfuller

    Cách 2, dùng adfuller test để kiểm tra tính ổn định của chuỗi. Bạn cần tải về thư viện statsmodels

pip install statsmodels

from statsmodels.tsa.stattools import adfuller

print(" > Is the data stationary ?")
dftest = adfuller(data, autolag='AIC')
print("Test statistic = {:.3f}".format(dftest[0]))
print("P-value = {:.3f}".format(dftest[1]))
print("Critical values :")
for k, v in dftest[4].items():
    print("\t{}: {} - The data is {} stationary with {}% confidence".format(k, v, "not" if v<dftest[0] else "", 100-int(k[:-1])))
    
print("\n > Is the de-trended data stationary ?")
dftest = adfuller(data_detrend.dropna(), autolag='AIC')
print("Test statistic = {:.3f}".format(dftest[0]))
print("P-value = {:.3f}".format(dftest[1]))
print("Critical values :")
for k, v in dftest[4].items():
    print("\t{}: {} - The data is {} stationary with {}% confidence".format(k, v, "not" if v<dftest[0] else "", 100-int(k[:-1])))
    
print("\n > Is the 12-lag differenced de-trended data stationary ?")
dftest = adfuller(data_season.dropna(), autolag='AIC')
print("Test statistic = {:.3f}".format(dftest[0]))
print("P-value = {:.3f}".format(dftest[1]))
print("Critical values :")
for k, v in dftest[4].items():
    print("\t{}: {} - The data is {} stationary with {}% confidence".format(k, v, "not" if v<dftest[0] else "", 100-int(k[:-1])))

 > Is the data stationary ?
Test statistic = 0.811
P-value = 0.992
Critical values :
	1%: -3.450632157720528 - The data is not stationary with 99% confidence
	5%: -2.870474482366864 - The data is not stationary with 95% confidence
	10%: -2.5715301325443787 - The data is not stationary with 90% confidence

 > Is the de-trended data stationary ?
Test statistic = -5.070
P-value = 0.000
Critical values :
	1%: -3.4514162625887037 - The data is  stationary with 99% confidence
	5%: -2.8708187088091406 - The data is  stationary with 95% confidence
	10%: -2.5717136883095675 - The data is  stationary with 90% confidence

 > Is the 12-lag differenced de-trended data stationary ?
Test statistic = -5.530
P-value = 0.000
Critical values :
	1%: -3.4521175397304784 - The data is  stationary with 99% confidence
	5%: -2.8711265007266666 - The data is  stationary with 95% confidence
	10%: -2.571877823851692 - The data is  stationary with 90% confidence

KPSS

    Cách 3, dùng KPSS test với giả thuyết rằng chuỗi có xu hướng ổn định. Nói cách khác, p-value < X% độ tin cậy => loại bỏ giả thuyết này, chuỗi không có xu hướng ổn định và ngược lại.

from statsmodels.tsa.stattools import kpss

print(" > Is the data stationary ?")
statistic, p_value, n_lags, critical_values = kpss(data)
print("Test statistic = {:.3f}".format(statistic))
print("P-value = {:.3f}".format(p_value))
print("num lags: {}".format(n_lags))
print("Critical values :")
for k, v in critical_values.items():
    print(f'   {k} : {v}')
print(f'Result: The series is {"not " if p_value < 0.05 else ""}stationary')

 > Is the data stationary ?
Test statistic = 1.902
P-value = 0.010
num lags: 17
Critical values :
   10% : 0.347
   5% : 0.463
   2.5% : 0.574
   1% : 0.739
Result: The series is not stationary

/python3.7/site-packages/statsmodels/tsa/stattools.py:1907: InterpolationWarning:
The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is smaller than the p-value returned.

warn_msg.format(direction="smaller"), InterpolationWarning

ACF & PACF

    Autocorrelation (ACF) plot là đồ thị thể hiện sự tương quan giữa chuỗi và độ trễ của chính nó.

    Partial autocorrelation (PACF) plot là đồ thị thể hiện số lượng tương quan giữa chuỗi và độ trễ, không tính mối tương quan với độ trễ thấp.

    Lý tưởng nhất là không có tương quan nào giữa chuỗi và độ trễ. Tức là chuỗi luôn cập nhật chính xác và kịp thời.

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

fig, ax = plt.subplots(2, figsize=(12,6))
ax[0] = plot_acf(data_detrend.dropna(), ax=ax[0], lags=20)
ax[1] = plot_pacf(data_detrend.dropna(), ax=ax[1], lags=20)

     Các cột vượt quá vùng xanh thể hiện mối tương quan với độ trễ 1, 2, 3, 4

Exponential Smoothing

    Phương pháp làm mịn này phù hợp với dữ liệu không theo xu hướng hoặc không theo chu kỳ.

    Các phương pháp làm mịn dữ liệu có phương thức cơ bản là tính trung bình cộng của quá khứ. Với những phương pháp nâng cao thì có thể thêm tính chu kỳ và tính xu hướng.

    Để dễ hiểu hơn, tôi sẽ giải thích bằng công thức toán học với y là chuỗi, p là kết quả dự đoán, l là giá trị p đã được smooth, s là giá trị chu kỳ và b là giá trị xu hướng.

Simple Exponential Smoothing

    Thuật toán này dùng khi ít dữ liệu, không có xu hướng và chu kỳ. Công thức ở đây là:

    $$p_t = l_t$$

    $$l_t = \alpha * y_t + (1-\alpha) * l_{t-1}$$

    Ở điểm ban đầu, lấy kết quả dự đoán ban đầu làm giá trị khởi tạo của l. Giá trị smooth ở thời điểm t = giá trị smooth ở thời điểm t-1 nhân với 1-$\alpha$ (thông số làm mịn) cộng với $\alpha$ nhân với giá trị quan sát ở thời điểm t-1.

from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt

train = data.iloc[:-10]
test = data.iloc[-10:]

model = SimpleExpSmoothing(np.asarray(train))

fit1 = model.fit()
pred1 = fit1.forecast(10)
fit2 = model.fit(smoothing_level=.2)
pred2 = fit2.forecast(10)
fit3 = model.fit(smoothing_level=.5)
pred3 = fit3.forecast(10)

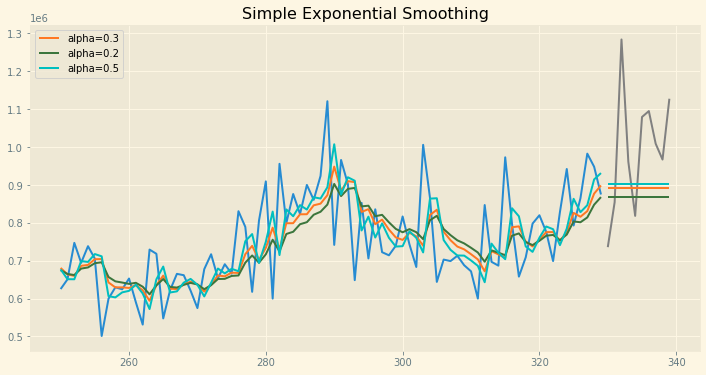
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(train.index[150:], train.values[150:])
ax.plot(test.index, test.values, color="gray")
for p, f, c in zip((pred1, pred2, pred3),(fit1, fit2, fit3),('#ff7823','#3c763d','c')):
    ax.plot(train.index[150:], f.fittedvalues[150:], color=c)
    ax.plot(test.index, p, label="alpha="+str(f.params['smoothing_level'])[:3], color=c)
plt.title("Simple Exponential Smoothing")    
plt.legend();

Holt’s Linear Smoothing

    Phương pháp làm mịn này phù hợp với dữ liệu theo xu hướng, không theo chu kỳ

    $$(1) Forecast p_{t+h|t} = l_t + b_t$$

    $$(2) l_t = \alpha * y_t + (1-\alpha) * l_{t-1} (\alpha = smoothing level)$$

    $$(3) b_t = \beta * (l_t - l_{t-1}) + (1-\beta) * b_{t-1} (\beta = smoothing slope)$$

from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt

train = data.iloc[:-10]
test = data.iloc[-10:]

model = Holt(np.asarray(train))

fit1 = model.fit(smoothing_level=.3, smoothing_trend=.05)
pred1 = fit1.forecast(10)
fit2 = model.fit(optimized=True)
pred2 = fit2.forecast(10)
fit3 = model.fit(smoothing_level=.3, smoothing_trend=.2)
pred3 = fit3.forecast(10)

fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(train.index[150:], train.values[150:])
ax.plot(test.index, test.values, color="gray")
for p, f, c in zip((pred1, pred2, pred3),(fit1, fit2, fit3),('#ff7823','#3c763d','c')):
    ax.plot(train.index[150:], f.fittedvalues[150:], color=c)
    ax.plot(test.index, p, label="alpha="+str(f.params['smoothing_level'])[:4]+", beta="+str(f.params['smoothing_trend'])[:4], color=c)
plt.title("Holt's Exponential Smoothing")
plt.legend();

    Dễ thấy ở đây, Holt's Linear cho ra kết quả tốt hơn một chút so với SES. Nhưng không thực tế do xu hướng tính bằng phương pháp này là hằng số không đổi trong tương lai (tăng đến vô hạn và giảm đến vô hạn). Vì vậy người ta nghĩ ra một cách là thêm một thông số để xu hướng hội tụ trong tương lai.

from statsmodels.tsa.holtwinters import ExponentialSmoothing
import numpy as np

model = ExponentialSmoothing(data), trend='mul', seasonal=None)
model2 = ExponentialSmoothing(data), trend='mul', seasonal=None, damped=True)
model._index = pd.to_datetime(train.index)

fit1 = model.fit()
fit2 = model2.fit()
pred1 = fit1.forecast(9)
pred2 = fit2.forecast(10)

fig, ax = plt.subplots(2, figsize=(12, 12))
ax[0].plot(train.index[250:], train.values[250:])
ax[0].plot(test.index, test.values, color="gray", label="truth")
ax[1].plot(train.index[300:], train.values[300:])
ax[1].plot(test.index, test.values, color="gray", label="truth")
for p, f, c in zip((pred1, pred2),(fit1, fit2),('#ff7823','#3c763d')):
    ax[0].plot(train.index[250:], f.fittedvalues[250:], color=c)
    ax[1].plot(train.index[300:], f.fittedvalues[300:], color=c)
    ax[0].plot(test.index, p, label="alpha="+str(f.params['smoothing_level'])[:4]+", beta="+str(f.params['smoothing_trend'])[:4]+ ", damping="+str(True if f.params['damping_trend']>0 else False), color=c)
    ax[1].plot(test.index, p, label="alpha="+str(f.params['smoothing_level'])[:4]+", beta="+str(f.params['smoothing_trend'])[:4]+ ", damping="+str(True if f.params['damping_trend']>0 else False), color=c)
ax[0].set_title("Damped Exponential Smoothing");
ax[1].set_title("Damped Exponential Smoothing - zoomed");
plt.legend();

    Còn phương pháp Holt-Winter’s Seasonal smoothing dành cho chuỗi theo chu kỳ nhưng tôi sẽ đề cập lần sau.

Kết luận

    Ở đây tôi sẽ không viết về ARIMA, các bạn có thể tham khảo blog của anh Khánh nếu muốn hiểu rõ hơn. Tổng thể cả bài tôi giới thiệu sơ qua định nghĩa về chuỗi thời gian và một số phương pháp làm mịn dữ liệu. Nhưng do lười nên tôi chỉ viết đến đây thôi, hẹn các bạn phần sau

Tham khảo

    https://phamdinhkhanh.github.io/2019/12/12/ARIMAmodel.html https://towardsdatascience.com/time-series-in-python-exponential-smoothing-and-arima-processes-2c67f2a52788 https://gitlab.fit.cvut.cz/marchan1/mvi-sp/tree/master => Lấy data về test thử