I. Cấu trúc dữ liệu `deque` - Hàng đợi hai đầu

1. Giới thiệu chung

Khi học lập trình C++, có lẽ chúng ta đều đã biết đến hai container stack và queue - hai cấu trúc dữ liệu ngăn xếp và hàng đợi được xây dựng sẵn trong thư viện STL C++. Nếu tưởng tượng cả hàng đợi và ngăn xếp được biểu diễn bằng mảng, thì hàng đợi sẽ hỗ trợ chúng ta lấy phần tử ra từ đầu mảng và thêm phần tử vào cuối mảng, còn ngăn xếp hỗ trợ chúng ta thêm và lấy ra phần tử từ cuối mảng.

Để khắc phục nhược điểm của stack và queue, người ta nghĩ ra một cấu trúc dữ liệu mới là hàng đợi hai đầu (deque). Hàng đợi hai đầu là sự kết hợp giữa stack và queue, hỗ trợ tất cả các thao tác thêm, xóa phần tử từ hai đầu hàng đợi với độ phức tạp vẫn là $O(1)$ . Sử dụng cấu trúc dữ liệu này sẽ thay thế được cả stack và queue, đồng thời lại rất dễ tưởng tượng hình vẽ.

*Mô tả hàng đợi hai đầu dưới dạng mảng*

2. Sử dụng hàng đợi hai đầu trong C++

Hàng đợi hai đầu đã được xây dựng sẵn trong STL C++, nên việc cài đặt lại là không cần thiết. Để sử dụng, trước tiên ta khai báo header queue cùng với không gian tên chuẩn (đối với các ngôn ngữ khác sẽ có các thư viện tương ứng):

#include <queue>

using namespace std;

Sau đó, khai báo theo cú pháp:

deque <{Kiểu_phần_tử}> {Tên_hàng_đợi};

Ví dụ: Khai báo một hàng đợi hai đầu chứa số nguyên:

deque < int > qu;

Bảng dưới đây sẽ cung cấp các phương thức được hỗ trợ của container deque:

Tên phương thức	Tác dụng	Độ phức tạp
`push_front(x)`	Thêm phần tử $x$ vào đầu hàng đợi	$O(1)$
`pop_front()`	Xóa một phần tử ở đầu hàng đợi	$O(1)$
`push_back(x)`	Thêm phần tử $x$ vào cuối hàng đợi	$O(1)$
`pop_back()`	Xóa một phần tử ở cuối hàng đợi	$O(1)$
`size()`	Trả về kích thước hiện tại của hàng đợi	$O(1)$
`empty()`	Trả về `true` nếu hàng đợi rỗng, ngược lại trả về `false`	$O(1)$
`front()`	Trả về phần tử ở đầu hàng đợi	$O(1)$
`back()`	Trả về phần tử ở cuối hàng đợi	$O(1)$

II. Kĩ thuật Tìm min - max trên đoạn tịnh tiến

Trong nhiều bài toán, các bạn sẽ cần phải tìm giá trị lớn nhất - nhỏ nhất trên một đoạn liên tục. Có nhiều phương pháp để làm việc này, chẳng hạn như sử dụng các cấu trúc dữ liệu Cây phân đoạn (Segment Tree) hay ***Cây chỉ số nhị phân (Binary Indexed Tree)***,...Tuy nhiên, nếu như đoạn cần kiểm tra là một đoạn dịch chuyển liên tục, thì kĩ thuật Deque Tìm min - max trên đoạn tịnh tiến thường được ưu tiên sử dụng vì sự đơn giản và độ phức tạp nhỏ.

Cấu trúc dữ liệu hàng đợi hai đầu sẽ được sử dụng trong kĩ thuật này. Tư tưởng của phương pháp dựa trên kĩ thuật Stack đơn điệu, chỉ lưu trữ các phần tử trong hàng đợi theo thứ tự tăng hoặc giảm, sao cho phần tử ở đầu hàng đợi luôn luôn là min hoặc max của đoạn đang xét. Lược đồ của phương pháp có thể mô tả như sau:

{Xét_đoạn_[l, r], định_thêm_r_vào_đoạn_đang_xét}
{
    // Lọc lại hàng đợi từ đầu.
    // Loại bỏ toàn bộ các phần tử ở đầu hàng đợi không thuộc đoạn [l, r].
    while (!deque.empty() && deque.front() not in [l, r])
        deque.pop_front();   
	
    // Lọc lại hàng đợi từ cuối.
    // Hàm comp(): Kiểm tra việc thêm r vào cuối hàng đợi có phá vỡ trật tự hay không.
    // Nếu có thì xóa các phần tử ở cuối hàng đợi tới khi không vi phạm nữa.
    while (!deque.empty() && !comp(deque.back(), r))
        deque.pop_back(); 
	
    // Thêm phần tử r vào cuối hàng đợi.
    deque.push_back(r);
}

Bây giờ, mình sẽ phân tích một số ví dụ cụ thể để giúp các bạn hiểu rõ hơn về kĩ thuật và cách áp dụng nó trong các bài toán!

Bài toán 1

Đề bài

Cho một mảng $A$ gồm $n \ (1 \le n \le 10^6)$ số nguyên $a_1, a_2,..., a_n \ (1 \le a_i \le 10^9)$ cùng với một số nguyên $k$ .

Yêu cầu: Hãy tìm giá trị lớn nhất trong các đoạn liên tiếp:

$a_1, a_2, \dots, a_k$ .
$a_2, a_3, \dots, a_{k + 1}$ .
$\dots$
$a_{n - k + 1}, a_{n - k + 2}, \dots, a_n$ .

Input:

Dòng đầu tiên chứa hai số nguyên dương $n$ và $k$ .
Dòng thứ hai chứa các số nguyên $a_1, a_2,..., a_n$ .

Output:

In ra $k$ số nguyên là giá trị lớn nhất của từng đoạn số

Sample Input

4 2
3 2 4 1

Sample Output

3 4 4

Ý tưởng

Cách làm đơn giản của bài toán này có độ phức tạp $O\big(k \times (n - k)\big),$ ta sẽ xét mọi đoạn con độ dài $k$ của dãy số và tìm ra giá trị lớn nhất của các đoạn con đó:

for (int i = k; i <= n; ++i)
{
    int max_range = a[i];
    for (int j = i - 1; j >= i - k + 1; --j)
        max_range = max(max_range, a[j]);

    cout << max_range << ' ';
}

Tất nhiên phương pháp này không thể giải quyết bài toán, ta cần một cách làm tốt hơn. Nhận xét thấy, khi xét một đoạn $[i - k + 1, i],$ thì giá trị lớn nhất của đoạn đó sẽ chỉ phụ thuộc vào những ô có giá trị giảm ngặt và vị trí tăng dần trong đoạn (các ô màu đỏ):

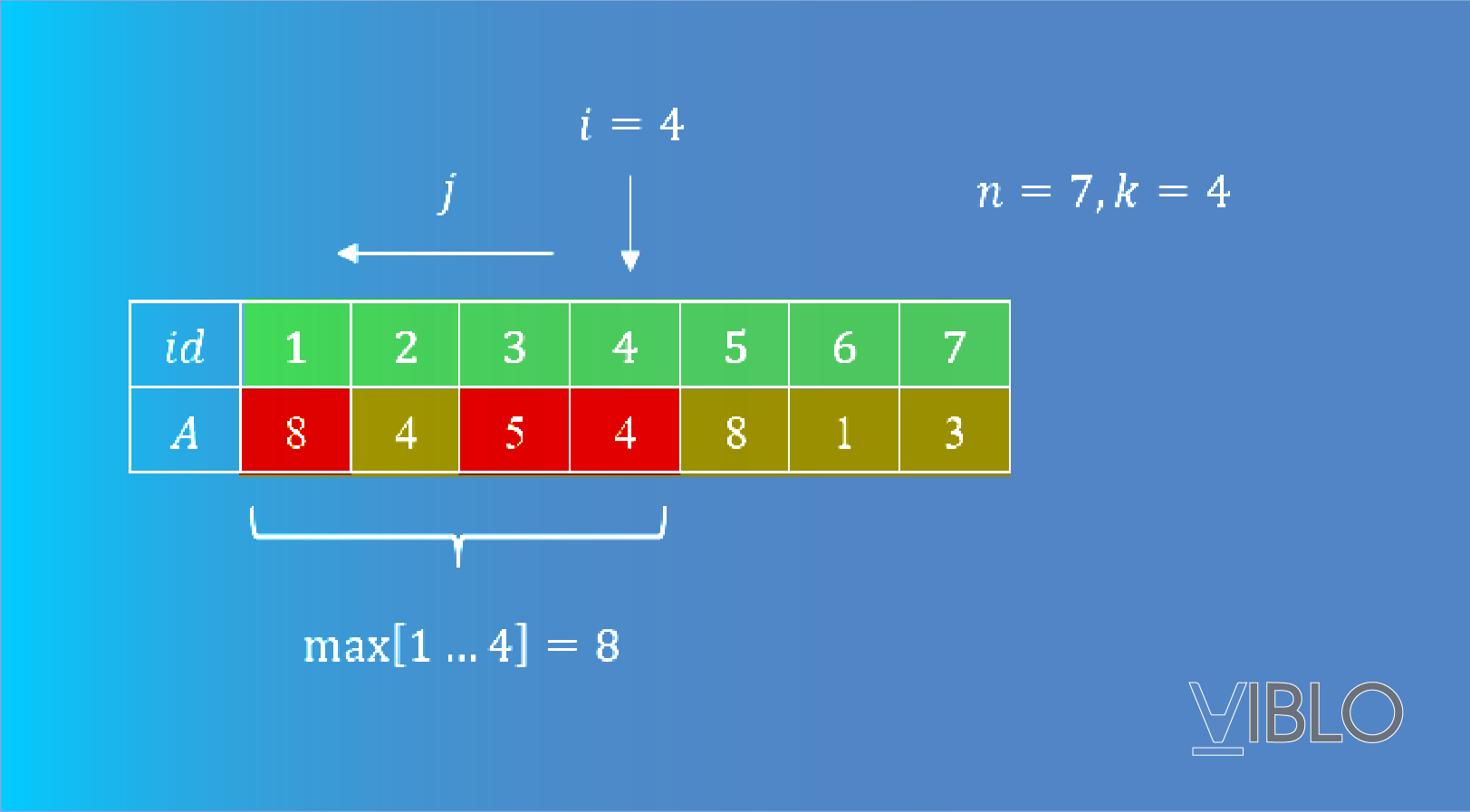
Nhận xét trên cho ta một ý tưởng về việc xây dựng một hàng đợi hai đầu chỉ lưu các ô có vị trí tăng dần và giá trị giảm dần trong đoạn đang xét. Nhờ thế, thông tin về phần tử lớn nhất trong đoạn sẽ được lưu ở vị trí front() của hàng đợi. Vậy ta thực hiện theo bốn bước như sau:

Đầu tiên khởi tạo một hàng đợi rỗng. Hàng đợi này dùng để lưu vị trí của các phần tử trong đoạn $[i - k + 1, i]$ .
Khi chuẩn bị đẩy một phần tử $i$ vào cuối hàng đợi, cần loại bỏ tất cả các phần tử ở cuối hàng đợi mà có giá trị nhỏ hơn hoặc bằng $a_i$ (để đảm bảo tính giảm ngặt về giá trị của các phần tử trong hàng đợi).
Loại bỏ toàn bộ các phần tử ở đầu hàng đợi có vị trí nhỏ hơn $i - k + 1,$ vì ta đang xét đoạn $[i - k + 1, i]$ . Thực tế, do việc tịnh tiến đoạn chỉ dịch về phía sau một vị trí, nên chỉ có tối đa một phần tử ở đầu hàng đợi bị loại đi.
Cuối cùng, phần tử ở đầu hàng đợi sẽ là vị trí của phần tử có giá trị lớn nhất trong đoạn. Lưu ý rằng, ta nên lưu trữ vị trí của các phần tử thay vì giá trị của chúng, như vậy sẽ dễ dàng hơn trong việc quản lý đoạn đang xét.

Lấy ví dụ với mảng ở hình vẽ bên trên, ta sẽ có quy trình lọc hàng đợi như sau (bạn đọc tự vẽ hình dựa theo mô tả để tưởng tượng):

Ban đầu khởi tạo hàng đợi rỗng. Đưa vị trí $1$ và $2$ vào hàng đợi.
Xét vị trí $3,$ ta có $a_3 = 5 > a[\text{deque.back()}],$ vì vậy loại bỏ phần tử $2$ trong deque đi rồi mới đưa $3$ vào.
Đưa vị trí $4$ vào hàng đợi.
Xét vị trí $i = 5,$ phần tử $1$ ở đầu hàng đợi sẽ bị loại đi do đoạn đang xét lúc này đã là $[2, 5],$ vị trí $1$ không còn thuộc đoạn nữa. Ngoài ra, do $a_5$ lớn hơn tất cả các phần tử trong hàng đợi hiện tại, nên toàn bộ hàng đợi sẽ bị loại đi từ cuối, rồi mới đưa vị trí $5$ vào.
Cứ tiếp tục thực hiện thuật toán như vậy mỗi khi xét tới một giá trị $i$ mới. Nếu như $i \ge k$ thì đoạn đang xét đã có đủ $k$ phần tử, lúc này in ra giá trị của phần tử ở đầu hàng đợi.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

int main()
{
    ios_base:sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n, k;
    cin >> n >> k;
	
    int a[n + 1];
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
	
    deque < int > qu_max;
    for (int i = 1; i <= n; ++i)
    {
        // Lọc các phần tử không thuộc đoạn [i - k + 1, i].
        while (!qu_max.empty() && a[qu_max.back()] <= a[i])
            qu_max.pop_back();

        // Lọc lại từ cuối deque để đảm bảo tính giảm ngặt.
        while (!qu_max.empty() && qu_max.front() < i - k + 1)
            qu_max.pop_front();

        qu_max.push_back(i);

        if (i >= k)
            cout << a[qu_max.front()] << ' ';
    }
	
    return 0;
}

Đánh giá

Độ phức tạp thuật toán: $O(n),$ do mỗi phần tử chỉ vào và ra khỏi deque không quá $1$ lần.

Chi phí lưu trữ: $O(n)$ .

Bài toán 2

Đề bài

Cho mảng $A$ gồm $n \ (1 \le n \le 10^5)$ số nguyên $a_1, a_2,..., a_n \ (1 \le a_i \le 10^9)$ .

Yêu cầu: Ứng với mỗi $a_i,$ hãy tìm đoạn $[l_i, r_i]$ dài nhất thỏa mãn:

$l_i \le i \le r_i$ .
$a_i$ là giá trị nhỏ nhất trong đoạn $a_l, a_{l + 1},..., a_r$ .

Input

Dòng đầu tiên chứa số nguyên dương $n$ .
Dòng thứ hai chứa $n$ số nguyên $a_1, a_2,..., a_n$ .

Output:

Ứng với mỗi $a_i,$ đưa ra cặp chỉ số $l_i, r_i$ tương ứng trên một dòng.

Sample Input

6
1 3 5 8 4 2

Sample Output

Ý tưởng

Xây dựng hai mảng $l, r$ sao cho ứng với mỗi $a_i$ thì:

$\begin{cases}l_i \le i \le r_i.\\ a_i = \text{min}(a_{l_i}, a_{l_i + 1}, \dots, a_{r_i}).\\ (r_i - l_i + 1) \ \text{max}. \end{cases}$

Cách làm đơn giản nhất ta có thể nghĩ ra là xét từng phần tử i và mở rộng phạm vi của $l_i$ và $r_i$ về hai bên. Cách làm này độ phức tạp $O(n^2),$ cài đặt như sau:

for (int i = 1; i <= n; ++i)
{
    l[i] = r[i] = i;
	
    while (l[i] > 0 && a[l[i] - 1] >= a[i])
    	--l[i];
    while (r[i] < n && a[r[i] + 1] >= a[i])
        ++r[i];
}

Với giới hạn $n \le 10^5,$ chắc chắn cách làm này không thể thỏa mãn yêu cầu đề bài. Ta cần một cách làm tốt hơn. Từ ý tưởng trên, các bạn có thể rút ra nhận xét như sau:

$(l_i - 1) = 0$ hoặc là số lớn nhất sao cho:

$\begin{cases}(l_i - 1) < i.\\ a_{l_i – 1} < a_i. \end{cases} \ (1)$
$(r_i + 1) = n + 1$ hoặc là số nhỏ nhất sao cho:

$\begin{cases}(r_i + 1) > i.\\ a_{r_i + 1} < a_i. \end{cases} \ (2)$

Từ hai nhận xét $(1)$ và $(2),$ ta sẽ cải tiến giải thuật bằng cách xây dựng hàng đợi hai đầu như sau: Trong khi duyệt các phần tử $a_i,$ ta sẽ đưa vị trí $i$ vào cuối deque, tuy nhiên trước đó cần phải loại bỏ tất cả các vị trí $j$ ở cuối deque mà $a_j \ge a_i$ . Tức là, ta sẽ có một deque gồm các giá trị vị trí sao cho các phần tử tương ứng ở vị trí đó trên mảng $A$ luôn luôn là tăng dần, đồng nghĩa với việc, giá trị ở front() của deque chính là giá trị thỏa mãn: $a_{\text{deque.front()}} = \text{min}(a_1, a_2, \dots, a_i)$ .

Lấy ví dụ, với mảng $A = \{1, 3, 5, 4, 2, 8\},$ việc lọc deque sẽ diễn ra như sau:

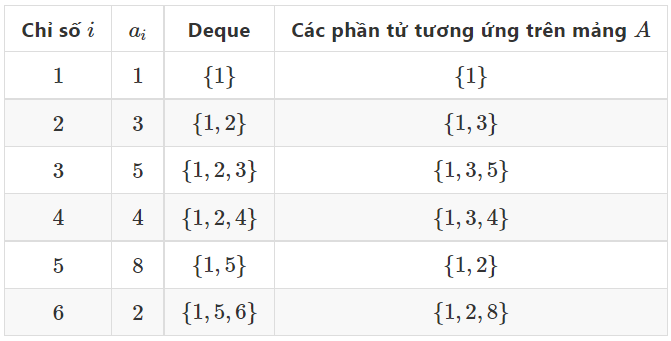
Bước lọc lại hàng đợi có thể mô tả như sau:

for (int i = 1; i <= n; ++i)
{
    while (!deque.empty() && a[deque.back()] >= a[i])
        deque.pop_back();
}

Mỗi khi lọc xong hàng đợi với một vị trí $i,$ ta có thể khẳng định $l_i = \text{deque.back()} + 1$ hoặc bằng $1$ . Thật vậy, do nhận xét $(1)$ phía trên, ta thấy $a_{l_i - 1} < a_i,$ do đó trong quá trình lọc lại deque, trước khi đưa $i$ vào cuối deque thì giá trị $(l_i – 1)$ sẽ không bị loại ra (vì ta chỉ loại các giá trị $j$ mà $a_j \ge a_i$ ). Vậy sau khi lọc xong deque, nó chỉ có thể ở một trong hai dạng: $\text{deque} = \{\dots, l_i - 1, i\};$ hoặc $\text{deque} = \emptyset$ . Nếu ở dạng $1,$ thì kết luận $l_i = \text{deque.back()} + 1,$ ngược lại thì $a_i$ chính là giá trị nhỏ nhất trong đoạn $[1, i],$ khi đó $l_i = 1$ .

Cuối cùng, đưa $i$ vào cuối hàng đợi theo đúng quy trình. Để xây dựng mảng $r,$ các bạn sẽ làm theo phương pháp tương tự, tuy nhiên cần duyệt các giá trị $i$ ngược từ $n$ về $1$ .

Cài đặt:

#include <bits/stdc++.h>

using namespace std;

const int maxn = 1e5 + 10;
int n, a[maxn], l[maxn], r[maxn];

void enter()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
	
    cin >> n;
	
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
}

void solve()
{
    deque < int > qu_min;

    for (int i = 1; i <= n; ++i)
    {
        while (!qu_min.empty() && a[qu_min.back()] >= a[i])
            qu_min.pop_back();
			
        l[i] = (qu_min.empty()) ? 1 : qu_min.back() + 1;
        quMin.push_back(i);
    }

    qu_min = deque < int > (); // reset lại deque về rỗng.
    for (int i = n; i >= 1; --i)
    {
        while (!qu_min.empty() && a[qu_min.back()] >= a[i])
            quMin.pop_back();
			
        r[i] = (qu_min.empty()) ? n : qu_min.back() - 1;
        quMin.push_back(i);
    }

    // In ra l[i], r[i] ứng với mỗi a[i].
    for (int i = 1; i <= n; ++i)
        cout << l[i] << ' ' << r[i] << endl;
}

int main()
{
    enter();
    solve();
    return 0;
}

Đánh giá

Độ phức tạp tính toán: Do mỗi phần tử sẽ được đẩy vào hàng đợi một lần và lấy ra khỏi hàng đợi cũng không quá một lần, nên độ phức tạp của quá trình lọc hàng đợi chỉ là $O(n)$ . Độ phức tạp tính toán tổng quát là $O(n)$ .

Chi phí lưu trữ: $O(n)$ .

Bài toán 3

Đề bài

Cho trước danh sách gồm $n \ (1 \le n \le 2 \times 10^5)$ quả bóng, mỗi quả bóng có số điểm là $a_i \ (1≤i≤n),$ và được cấp $k \ \big(1 \le k \le \text{min}(n, 200)\big)$ lượt chơi bắn bóng. Ở mỗi lượt chơi, người chơi được quyền chọn một quả bóng để bắn. Gọi $p_j$ là số hiệu của quả bóng bị bắn ở lượt thứ $j \ (1≤j≤k),$ thì số điểm người chơi nhận được ở lượt đó sẽ là $j×a_{p_j}$ . Tuy nhiên, trò chơi có một quy tắc lựa chọn bong bóng để bắn như sau: Ở lượt chơi thứ $j \ (1<j≤k)$ thì $1≤p_j-p_{j - 1}≤m \ (1 \le m \le n)$ .

Yêu cầu: Hãy tính tổng số điểm lớn nhất mà người chơi có thể giành được sau $k$ lượt chơi?

Input

Dòng đầu tiên chứa hai số nguyên dương $n, m$ và $k$ – số quả bóng, hằng số $m$ và số lượt chơi người chơi được cung cấp.
Dòng thứ hai chứa $n$ số nguyên dương $a_1,a_2,…,a_n$ – số điểm được ghi trên các quả bóng.

Output

Một số nguyên duy nhất là tổng số điểm lớn nhất người chơi giành được.

Sample Input

7 1 3
1 9 2 4 5 3

Sample Output

Ý tưởng

Đây là một bài toán sử dụng quy hoạch động. Đặt $dp[i][j]$ là số điểm lớn nhất dành được khi chơi $i$ lượt, chọn quả bóng thứ $j$ để bắn ở lượt thứ $i$ . Theo đề bài, do lượt thứ $i$ đã chọn quả bóng thứ $j,$ nên lượt thứ $i - 1$ chỉ được phép chọn các quả bóng trong đoạn $[i - m, i - 1]$ . Từ đây dễ dàng hình thành công thức truy hồi:

$dp[i][j] = \text{max}(dp[i - 1][(j - 1)...(j - M)]) + a[j] \times i$

Nếu như dùng hai vòng lặp để tính các $dp[i][j]$ thì độ phức tạp thuật toán sẽ lên tới $O(m \times n),$ không thể đáp ứng được yêu cầu thời gian. Ta cải tiến như sau: Nhận thấy $dp[i][j]$ luôn được cập nhật từ những đoạn tịnh tiến trên $dp[i - 1][k],$ sử dụng kĩ thuật deque min - max trên đoạn tịnh tiến để tìm ra các $dp[i - 1][k]$ lớn nhất với $k = (j - 1)...(j - m),$ rồi cập nhật cho $dp[i][j]$ .

Về cơ sở quy hoạch động, ta khởi tạo trước $dp[i][0] = -\infty,$ thể hiện rằng không tồn tại $dp[i][0]$ và các bài toán được cập nhật từ $dp[i][0]$ cũng sẽ là các bài toán không tồn tại cách chơi.

Cài đặt

#include <bits/stdc++.h>
#define int long long
#define inf 1e15

using namespace std;

const int maxn = 2e5 + 10, maxk = 201;
int n, m, k, a[maxn], dp[maxk][maxn];

void enter()
{
    cin >> n >> m >> k;

    for (int i = 1; i <= n; ++i)
        cin >> a[i];
}

void solution()
{
    dp[1][0] = -inf;
    for (int j = 1; j <= n; ++j) // Cơ sở quy hoạch động dp[1][j] = a[j];
        dp[1][j] = a[j];

    for (int i = 2; i <= k; ++i)
    {
        dp[i][0] = -inf;

        deque < int > qu_max;
        for (int j = 1; j <= n; ++j)
        {
            while (!qu_max.empty() && qu_max.front() < j - m)
                qu_max.pop_front();

            while (!qu_max.empty() && dp[i - 1][qu_max.back()] <= dp[i - 1][j - 1])
                qu_max.pop_back();
            qu_max.push_back(j - 1);

            dp[i][j] = dp[i - 1][qu_max.front()] + a[j] * i;
        }
    }

    int res = *max_element(dp[K], dp[K] + 1 + N);
    cout << res;
}

main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    enter();
    solution();

    return 0;
}

Đánh giá

Độ phức tạp thuật toán: $O(n \times k)$ .

Chi phí lưu trữ: $O(n \times k)$ .

III. Tổng kết

Như vậy, mình đã hướng dẫn các bạn toàn bộ lý thuyết cũng như các bài tập tiêu biểu của kĩ thuật Deque tìm Min - Max trên đoạn tịnh tiến. Ưu điểm của kĩ thuật này là cài đặt dễ, tốc độ thực hiện nhanh và có thể áp dụng vào cải tiến tốc độ của rất nhiều bài toán khác nhau, đặc biệt là các bài toán quy hoạch động có công thức truy hồi liên quan tới các đoạn tịnh tiến.

Tuy nhiên, kĩ thuật này cũng có một nhược điểm, đó là không thể áp dụng với các bài toán mà dãy số bị cập nhật liên tục (nói cách khác, kĩ thuật chỉ sử dụng cho các bài toán xử lý offline). Lí do là vì, giả sử có $m$ thao tác cập nhật dãy số, thì mỗi lần cập nhật ta lại phải tính lại $\text{min, max}$ của từng đoạn, dẫn đến độ phức tạp trở thành $O(n \times m)$ . Trong trường hợp này, các bạn cần áp dụng cấu trúc dữ liệu Cây phân đoạn (Segment Tree).

Ngoài ra, có một lỗi nho nhỏ mà các bạn có thể mắc phải khi cài đặt kĩ thuật, đó là không kiểm tra hàng đợi có rỗng hay không (empty). Nếu hàng đợi rỗng mà vẫn lấy các vị trí front() hoặc back() thì sẽ bị lỗi. Hãy lưu ý điều này khi lập trình!

Các bạn có thể luyện tập thêm kĩ thuật này thông qua một số bài tập dưới đây:

I. Cấu trúc dữ liệu `deque` - Hàng đợi hai đầu

1. Giới thiệu chung

2. Sử dụng hàng đợi hai đầu trong C++

II. Kĩ thuật Tìm min - max trên đoạn tịnh tiến

Bài toán 1

Đề bài

Ý tưởng

Cài đặt

Đánh giá

Bài toán 2

Đề bài

Ý tưởng

Đánh giá

Bài toán 3

Đề bài

Ý tưởng

Cài đặt

Đánh giá

III. Tổng kết

IV. Tài liệu tham khảo

Tìm số ước của một số với độ phức tạp O(N^1/3)

Xử lý số nguyên lớn (phần 2) - Các phép toán Nhân

Một số thuật toán cơ bản được ứng dụng trong an toàn thông tin (Phần 2)

Tối ưu đoạn tịnh tiến với deque và tìm min-max

Geometric Computing Challenges in Competitive Programming

Giới thiệu thuật toán tìm kiếm nhị phân

Giới thiệu về lý thuyết trò chơi (phần 2)

Tìm kiếm dữ liệu nhanh với mẹo tìm kiếm nhị phân

Giới thiệu về Lý thuyết đồ thị

Matrix Exponentiation - Simplifying Complex Calculations

I. Cấu trúc dữ liệu deque - Hàng đợi hai đầu

1. Giới thiệu chung

2. Sử dụng hàng đợi hai đầu trong C++

II. Kĩ thuật Tìm min - max trên đoạn tịnh tiến

Bài toán 1

Đề bài

Ý tưởng

Cài đặt

Đánh giá

Bài toán 2

Đề bài

Ý tưởng

Đánh giá

Bài toán 3

Đề bài

Ý tưởng

Cài đặt

Đánh giá

III. Tổng kết

IV. Tài liệu tham khảo

Tìm số ước của một số với độ phức tạp O(N^1/3)

Xử lý số nguyên lớn (phần 2) - Các phép toán Nhân

Một số thuật toán cơ bản được ứng dụng trong an toàn thông tin (Phần 2)

Tối ưu đoạn tịnh tiến với deque và tìm min-max

Geometric Computing Challenges in Competitive Programming

Giới thiệu thuật toán tìm kiếm nhị phân

Giới thiệu về lý thuyết trò chơi (phần 2)

Tìm kiếm dữ liệu nhanh với mẹo tìm kiếm nhị phân

Giới thiệu về Lý thuyết đồ thị

Matrix Exponentiation - Simplifying Complex Calculations

I. Cấu trúc dữ liệu `deque` - Hàng đợi hai đầu