Lời Giới Thiệu

    Các mô hình Deep Convolutional Neural Networks (DCNN) đã trở thành một lựa chọn thường nhật cho việc bóc tách các đặc điểm của khuôn mặt và đã chứng tỏ được các ưu thế vượt trội trong công việc này. Và việc còn lại đó là khiến cho các véc tơ mang đặc điểm này được phân loại tốt nhất giúp cho việc nhận diện khuôn mặt trở nên chính xác hơn. Có hai hướng chính để thực hiện việc đó, có người sẽ ưu tiên việc tạo thêm một mô hình phân loại, giả sử như sử dụng softmax, hay có người sẽ lựa chọn huấn luyện máy trực tiếp sử dụng những véc tơ embeddings, như sử dụng hàm mất mát triplet. Tuy rằng cả hai phương pháp đã cho thấy những kết quả rất tốt nhưng chúng vẫn còn tồn tại một số những khuyết điểm đáng để nhắc đến. Việc sử dụng hàm softmax khiến cho kích thước của ma trận biến đổi tuyến tính tăng tỉ lệ với số lượng danh tính mà chúng ta muốn phân loại, đồng thời việc huấn luyện theo phương pháp này khiến mô hình phân loại khá tốt với những vấn đề phân loại kín (khi mà tập hợp đầu vào và tập hợp đầu ra có chung số lượng class) cho thấy phương pháp này là không quá thực tế khi số lượng khuôn mặt khác nhau (số lượng class ) mà chúng ta cần nhận diện thường thay đổi. Hàm triplet loss xử lí được vấn đề này nhưng nó cũng tồn tại những khuyết điểm riêng. Vì triplet loss được lấy ý tưởng từ việc so sánh 3 mẫu một lần nên với số lượng dữ liệu tăng lên, số lượng bộ 3 cũng sẽ tăng theo cấp số nhân dẫn đến số lượng vòng lặp cũng tăng đáng kể, hơn nữa, giải pháp được cho là tối ưu khi huấn luyện với triplet loss là semi-hard sample training thì khá là khó để huấn luyện hiệu quả. Vì những khuyết điểm này mà các nhà nghiên cứu đã đưa ra một hướng đi mới cho việc nhận diện khuôn mặt với việc giới thiệu một hàm mất mát mới Additive Angular Margin Loss.

Phương Hướng Tiếp Cận

    Hàm mất mát Additive Angular Margin Loss có thể được xem như một sự cải tiến cho hàm softmax, tích vô hướng giữa véc tơ đặc điểm từ mô hình DCNN và lớp fullly connected cuối bằng với khoảng cách cosine của feature và weight đã được chuẩn hóa. Chúng ta tận dụng hàm arc-cosine để tính góc giữa feature hiện tại và weight mục tiêu . Sau đó chúng ta cộng thêm additive angular margin vào góc mục tiêu và chúng ta sẽ thu được lại véc tơ logit thông qua hàm cosine. Tiếp theo, các logits sẽ được định lại tỉ lệ và các bước còn lại sẽ giống hệt như hàm mất mát softmax. Ảnh dưới đây minh họa quá trình vừa đề cập:

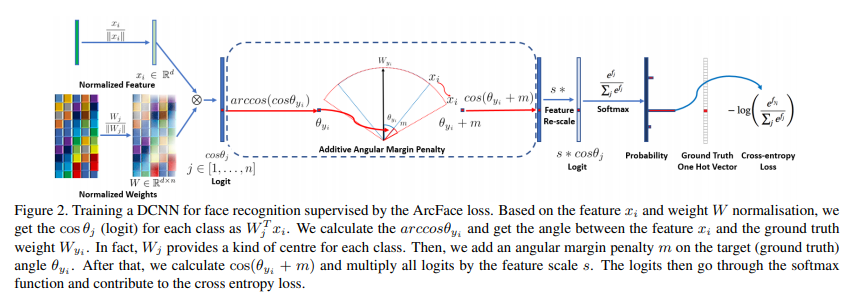
    Vậy để hiểu được kĩ hơn phương pháp mới này, chúng ta sẽ đi từ những thứ quen thuộc nhất, bắt đầu với hàm softmax với công thức:

    $$L_{\substack{1}} = -\frac 1 N \sum_{\substack{i=1}} ^N log \frac {e^{W_{\substack{y_i}}^T x_i + b_{\substack{y_i}}}} {\sum_{\substack{j=1}}^n e^{W_{\substack{j}}^T x_i + b_j} }$$

    Có thể hiểu đơn giản hàm mất mát softmax là sự kết hợp giữa hàm mất mát entropy chéo và sự kích hoạt softmax (softmax activation). Hàm này trong quá khứ thường được sử dụng cho các bài toán nhận diện khuôn mặt. Tuy nhiên, điểm yếu của hàm này đó là không có khả năng tối ưu hóa rõ ràng các véc tơ embedding chứa các đặc điểm của khuôn mặt để tăng thêm sự tương đồng giữa những khuôn mặt trong một lớp và tăng thêm sự đa dạng giữa các khuôn mặt giữa các lớp, dẫn đến tạo ra 1 khoảng cách cho những khuôn mặt với nhiều biến thể (do khác biệt tuổi tác hay do khác biệt về dáng khuôn mặt).

    Để đơn giản hóa, chúng ta cố định bias $b_j = 0$, sau đó chúng ta biến đổi $W_{\substack{j}}^T x_i = \text{\textbardbl} W_j \text{\textbardbl} \text{\textbardbl}x_i\text{\textbardbl} \cos \theta_j$ trong đó $\theta_j$ là góc giữa weight $W_j$ và đặc điểm $x_i$. Theo sau đó, chúng ta cố định weight $\text{\textbardbl}W_j\text{\textbardbl}=1$ bởi sự chuẩn hóa L2. Đồng thời, chúng ta cũng chuẩn hóa luôn véc tơ đặc điểm $\text{\textbardbl}x_i\text{\textbardbl}$ theo sự chuẩn hóa L2 và rescale lại thành s. Bước chuẩn hóa weights và véc tơ đặc điểm này tạo nên sự dự đoán thuần túy dựa trên góc giữa véc tơ đặc điểm và weight. Véc tơ đặc điểm đã được học sau đó được phân bổ trên một hypersphere với bán kính là s.

    $$L_2 = -\frac{1} {N} \sum_{\substack{i=1}} ^N log \frac {e^{s \cos \theta_{\substack{y_i}}}} {e^{s \cos \theta_{\substack{y_i}}} + \sum_{\substack{j=1, j{=}\mathllap{/\,}y_i}}^n e^{s \cos \theta_{\substack{j}}}}$$

    Vì các véc tơ đặc điểm được phân bổ xung quanh mỗi đặc điểm trung tâm theo một hypersphere, chúng ta sẽ thêm vào đó một hình phạt biên góc cộng (additive angular margin penalty) m giữa $x_i$ và $W_{\substack{y_i}}$ để đồng thời tăng cường tính nhỏ gọn trong nội bộ lớp và sự khác biệt giữa các lớp. Và phương pháp này được đặt tên là ArcFace.

    $$L_3 = -\frac {1} {N} \sum_{\substack{i=1}} ^N log \frac { e^{s (\cos(\theta_{\substack{y_i}} + m))} } { e^{s (\cos(\theta_{\substack{y_i}} + m))} + \sum_{\substack{j=1, j{=}\mathllap{/\,}y_i}}^n e^{s \cos \theta_{\substack{j}}} }$$

    Theo như paper, chúng ta sẽ chọn khoảng chừng 1500 ảnh cho 1 khuôn mặt với tổng cộng 8 khuôn mặt khác nhau để huấn luyện mạng với lần lượt hàm softmax và hàm mất mát ArcFace. Kết quả thu được được minh hoa theo ảnh dưới đây:

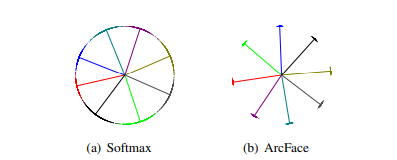
    Theo như hình, ta có thể thấy việc sử dụng softmax với hàm mất mát entropy chéo giúp chúng ta phân tách các véc tơ đặc điểm tuy nhiên lại tạo nên 1 sự mơ hồ rõ ràng trên đường ranh giới quyết định (decision boudaries). Trong khi đó, sử dụng softamx với hàm mất mát ArcFace lại có sự phân chia rõ rệt giữa các lớp gần nhau.

Một số kết luận cá nhân

    Theo như mình thấy mô hình ArcFace đạt được kết quả nhận diện với độ chính xác cao. Và một ưu điểm hơn cả khi so sánh với triplet loss của Facenet là hàm mất mát ArcFace dễ triến khai trên code hơn, chúng ta có thể tùy chỉnh hàm để kết hợp cùng với rất nhiều các mô hình CNN hiện có để tạo ra một mô hình nhận diện khuôn mặt phù hợp nhất với yêu cầu cá nhân.