Có thể nói rằng thành công gần đây của của các mô hình Deep Learning một phần được thúc đẩy bởi việc huấn luyện trên các bộ dữ liệu có kích cỡ ngày càng lớn. Tuy vậy, đôi khi hẳn ta sẽ tự hỏi kiểu như "Liệu bao nhiêu dữ liệu trong 10 triệu mẫu kia là không cần thiết?", "Liệu có những mẫu dữ liệu nào quan trọng cho việc tổng quát hóa không và ta tìm thấy chúng như thế nào? Bài viết này trình bày kết quả nghiên cứu được công bố trong bài báo Deep Learning on a Data Diet: Finding Important Examples Early in Training bao gồm việc đề xuất phương pháp xác định sớm một tập dữ liệu đào tạo nhỏ hơn đáng kể trong quá trình đào tạo, có thể được sử dụng để đạt được độ chính xác của bài kiểm tra tương đương với đào tạo trên tập dữ liệu đầy đủ.

Mở đầu

    Trong thời gian qua, Deep Learning đã đạt được những tiến bộ đáng kể, một phần là do đào tạo các overparameterized model trên các bộ dữ liệu lớn hơn bao giờ hết. Xu hướng này tạo ra những thách thức mới: nhu cầu về. nguồn lực tính toán lớn cần thiết đặt ra một rào cản cho quá trình dân chủ hóa AI (democratization of AI, có vẻ như ý của nhóm tác giả là việc thiếu hụt dữ liệu và tài nguyên khiến cho các tổ chức và cá nhân không có nguồn lực đủ lớn khó có thể cài đặt và kiểm tra các ý tưởng của mình một cách hiệu quả). Tiếp đó, các hạn chế về bộ nhớ và tài nguyên, chẳng hạn như on-device computing, yêu cầu các mô hình và bộ dữ liệu cần có kích thước nhỏ hơn. Bởi vậy nên, việc xác định dữ liệu đào tạo quan trọng hiệu quả sẽ góp phần quan trọng trong việc cải thiện hiệu năng của online learning và active learning.

    Nghiên cứu gần đây liên quan đến pruning data, có thể được đặt trong bối cảnh rộng hơn là xác định các bộ lõi cho phép đào tạo với độ chính xác gần như có thể với dữ liệu gốc. Các công trình này cố gắng xác định các mẫu có thể đảm bảo một khoảng cách nhỏ về lỗi đào tạo trên tập dữ liệu đầy đủ. Tuy nhiên, do bản chất không lồi của học sâu, các kỹ thuật này đưa ra các ước tính thận trọng dẫn đến đảm bảo lý thuyết yếu và kém hiệu quả hơn trong thực tế. Các nghiên cứu được trích dẫn bao gồm: sử dụng một mô hình proxy nhỏ để thực hiện việc lựa chọn dữ liệu (mẫu: chọn các điểm dữ liệu để gắn nhãn cho việc active learning) thông qua việc loại bỏ các lớp ẩn khỏi mô hình đích, sử dụng các kiến trúc nhỏ hơn và đào tạo với số epoch thấp hơn như trong Selection via Proxy: Efficient Data Selection for Deep Learning hay đề xuất một phương pháp mang tên Data Distribution Search (DDS, tìm kiếm phân phối dữ liệu), để lựa chọn đồng đều trên tất cả các vùng dựa trên phân phối dữ liệu trong Data Distribution Search to Select Core-Set for Machine Learning

    Một cách tiếp cần khác được trình bày trong Deep learning versus kernel learning: an empirical study of loss landscape geometry and the time evolution of the Neural Tangent Kernel là theo dõi số lần thông qua việc huấn luyện một mẫu chuyển đổi từ được phân loại chính xác sang phân loại sai, được gọi là "forgetting event" và nhận thấy rằng một số mẫu hiếm khi bị quên, trong khi những mẫu khác bị quên lặp đi lặp lại. Theo kinh nghiệm, họ quan sát thấy rằng độ chính xác của quá trình huấn luyện không bị ảnh hưởng bởi các mẫu huấn luyện hiếm khi bị quên và một phần lớn dữ liệu huấn luyện có thể được loại bỏ mà không ảnh hưởng đến độ chính xác. Tuy nhiên, vì phương pháp này dựa vào việc thu thập số liệu thống kê về sự quên trong suốt quá trình huấn luyện, nên điểm số quên thường được tính vào giữa hoặc cuối quá trình huấn luyện. Toneva và cộng sự thấy rằng, trong mẫu của họ về ResNet18 được đào tạo trên CIFAR-10 trong 200 epochs, Spearman rank correlation giữa điểm sớm và điểm muộn là tốt sau khoảng 25 epochs và ổn định sau 75 epochs.

    Được trình bày trong bài báo cũng như phần thuyết trình của nhóm tác giả, nội dung của bài báo xoay quanh những điều sau:

• Dữ liệu đóng vai trò như thế nào trong việc huấn luyện các mô hình?
• Bản chất của các mẫu có thể được xóa khỏi dữ liệu đào tạo mà không ảnh hưởng đến độ chính xác là gì?
• Làm thế nào sớm trong quá trình đào tạo, chúng ta có thể nhận ra những mẫu như vậy?
• Chúng ta cần bao nhiêu mẫu và điều này phụ thuộc vào việc phân phối dữ liệu như thế nào?

    Chi tiết nội dung sẽ được trình bày ở các phần tiếp theo

Những mẫu nào quan trọng cho việc học?

Cụ thể hóa bài toán

    Để cụ thể hơn bài toán cần xác định, nhóm tác giả xét bài toán phân loại ảnh có giám sát với tập dữ liệu $S = \{ \left ( x _{ i }, y_ { i } \right ) \} _ { i = 1 } ^ { N }$ độc lập và có phân bố đồng nhất từ một phân bố dữ liệu chưa biết $\mathcal{D}$, với vector đầu vào $x \in \mathcal{R} ^ { d }$ và vector one-hot $y \in {\{0, 1 \}}^k$ là nhãn đã được encode.

    Đối với kiến trúc mạng nơron cố định, đặt $\mathcal{f}_w (x) \in \cal{R}^K$ là đầu ra logit của mạng nơron có trọng số $w ∈ \mathcal{W} ⊆ \mathcal{R}^D$ trên đầu vào $x ∈ \mathcal{R}^d$. Gọi $\sigma$ là hàm softmax cho bởi $\sigma \left ( z_ { 1 }, \ldots, z _{ K } \right )_ { k } = \exp \{ z _{ k } \} / \sum_ { k ^ { \prime } = 1 } ^ { K } \exp \{ z _{ k ^ { \prime } } \}$. Với $p \left ( w, x \right ) = \sigma \left ( f \left ( w, x \right ) \right )$ biểu thị đầu ra của mạng nơ-ron ở dạng vectơ xác suất. Đối với bất kỳ vectơ xác suất $\hat{p}$ nào, ta có hàm lỗi cross-entropy $\ell \left ( \hat { p }, y \right ) = \sum_ { k = 1 } ^ { K } y ^ { \left ( k \right ) } \log \hat { p } ^ { \left ( k \right ) }$.

    Cho $\bold{w} _{ 0 }, \bold{w}_ { 1 }, \ldots,\bold{w} _{ T }$ là số lần lặp lại của stochastic gradient descent (SGD), trong đó, đối với một số chuỗi minibatch $S_ { 0 }, S _{ 1 }, \ldots, S_ { T - 1} \subseteq S$ có kích thước M, ta có:

    $$w _ { t } = w _ { t - 1 } - \eta \sum _ { \left ( x, y \right ) \in S _ { t - 1 } } g _ { t - 1 } \left ( x, y \right ), \quad$$

    Với mọi $g _{ t - 1 } \left ( x, y \right ) = \nabla_ { w _{ t - 1 } } \ell \left ( p \left ( w_ { t - 1 }, x \right ), y \right ),$ và $t = 1, \ldots, T.$

Điểm Gradient Norm và một vài phân tích nho nhỏ

    Với tập huấn luyện $S$ được cố định, do được đào tạo với SGD từ lần khởi tạo ngẫu nhiên, vectơ trọng số tại thời điểm $t> 0$, $\bold{w}_t$, là một biến ngẫu nhiên. Độ lớn dự kiến của vectơ giá trị hàm lỗi là trọng tâm chính được xem xét trong bài báo. Quá trình này xoay quanh việc xem xét điểm Gradient Norm (GraNd) được định nghĩa như sau:

    Định nghĩa: Với mẫu huấn luyện $(x, y)$ tại điểm $t$ được định nghĩa thông qua công thức $\chi _{ t } \left ( x, y \right ) = { \operatorname { E } }_ { w _{ t } } \| g_ { t } \left ( x, y \right ) \| _ { 2 }.$

    Thông việc xem xét giá trị này, nhóm tác giả cho rằng chúng định lượng (hoặc ít nhất là kiểm soát) sự đóng góp của một mẫu đào tạo vào sự thay đổi của hàm lỗi trong quá trình huấn luyện.

    Một đại lượng quan trọng trong phân tích là đạo hàm theo thời gian của tổn thất đối với mẫu được dán nhãn chung $(x, y): \Delta _{ t } \left ( \left ( x, y \right ), S_ { t } \right ) = - \frac { d \ell \left ( f _{ t } \left ( x \right ), y \right ) } { d t }$ (trong đó $f_ { t } \left ( \cdot \right ) = f _{ w t } \left ( \cdot \right )$), tức là tốc độ thay đổi tức thời của tổn thất trên $(x, y)$ tại thời điểm $t$, trong đó gradient được tính trên minibatch $S_t$. Theo quy tắc chuỗi,

    $$\Delta_ { t } \left ( \left ( x, y \right ), S _{ t } \right ) = g_ { t } \left ( x, y \right ) \frac { \operatorname { d w } _ { t } } { \operatorname { d t } }.$$

    Điều này liên quan đến động lực học thời gian rời rạc của chúng ta thông qua $\frac { \operatorname { d w } _{ t } } { \operatorname { d t } } \approx \operatorname { w }_ { t + 1 } - w _{ t } = - \eta \sum_ { \left ( x ^ { \prime }, y ^ { \prime } \right ) \in S _{ t - 1 } } g_ { t - 1 } \left ( x ^ { \prime }, y ^ { \prime } \right )$

    Mục tiêu của ta là hiểu cách việc xóa một điểm đào tạo khỏi minibatch $S_t$ ảnh hưởng đến $\Delta _{ t }\left ( \left ( x, y \right ), S_ { t }\right )$

    Bổ đề: Cho $S _{ \neg j } = S \backslash \left ( x_ { j }, y _{ j } \right )$. Khi đó tồn tại mẫu $(x, y)$ để tồn tại $c$ sao cho:

    $$\| \Delta_ { t } ( ( ( x, y ), S ) - \Delta _{ t } ( ( ( x, y ), S_ { - j } ) \| \leq c \| gv _{ t } ( x_ { j }, y _ { j } ) \|.$$

    => Chứng minh: Đối với một mẫu cụ thể x, quy tắc chuỗi cho ra $\Delta _{ t } \left ( \left ( x, y \right ), S \right ) = - \frac { d \ell \left ( f_ { t } \left ( x \right ), y \right ) } { d t } = \frac { d \ell \left ( f _{ t } \left ( x \right ), y \right ) } { \operatorname { d w }_ { t } } \frac { d w _{ t } } { d t }$. Vì các trọng số được cập nhật bằng SGD nên ta có $\frac { \operatorname { d w }_ { t } } { d t } = - \eta \sum _{ \left ( x_ { j }, y _{ j } \right ) \in S_ { t } } g _{ t } \left ( x_ { j }, y _{ j } \right )$. Đặt $c = \eta | | \frac { \operatorname { d \ell } \left ( f_ { t } \left ( x \right ), y \right ) } { \operatorname { d w } _ { t } } | |$, và ta có được kết quả như trên.

    Tại bất kỳ bước đào tạo nhất định nào, với vị trí hiện tại $\bold{w}_t$, đóng góp của một mẫu đào tạo $(x, y)$ vào việc giảm tổn thất trên bất kỳ mẫu nào khác, được giới hạn bởi Công thức được trình bày trong bổ đề. Vì hằng số $c$ không phụ thuộc vào $(x, y)$ nên ta chỉ xét gradient norm, $\| g_t{(x, y)}\|$. Giá trị kỳ vọng của định mức gradient này chính xác là điểm GraNd của $(x, y)$. Nói cách khác, các mẫu có điểm GraNd nhỏ trong kỳ vọng có ảnh hưởng nhất định đến việc học cách phân loại phần còn lại của dữ liệu đào tạo tại một thời điểm đào tạo nhất định. Do đó, nhóm tác giả đề xuất xếp hạng các mẫu đào tạo theo điểm GraNd của chúng, định mức lớn hơn có nghĩa là quan trọng hơn để duy trì $\Delta_t (x)$.

    Đối với một đầu vào tùy ý $x \in \operatorname { E } ^ { d }$, ta có $\psi _{ t } ^ { \left ( k \right ) } \left ( x \right ) = \nabla_ { w _{ t } } f_ { t } ^ { \left ( k \right ) } \left ( x \right )$ biểu thị gradient logit thứ $k$. Sau đó, GraNd có thể được viết là:

    $$\chi _ { t } \left ( x, y \right ) = \operatorname { E } \left \| \sum _ { k = 1 } ^ { K } \nabla _ { f } \left ( k \right ) \ell \left ( f _ { t } \left ( x \right ), y \right ) ^ { T } \psi _ { t } ^ { \left ( k \right ) } \left ( x \right ) \right \| _ { 2 }$$

    Theo giá trị hàm lỗi entropy chéo, $\nabla _{ f \left ( k \right ) } \ell \left ( f_ { t } \left ( x \right ), y \right ) ^ { T } = p \left ( w _{ t }, x \right ) ^ { \left ( k \right ) } - y_ { k }$. Khi $\{ \psi _{ t } ^ { \left ( k \right ) } \left ( x \right ) \}_ { k }$ gần như trực giao trên các logits và có cùng kích thước trên các logits và mẫu huấn luyện $x$, thì chúng ta có thể tính gần đúng GraNd chỉ bằng chuẩn của vector lỗi. Khi đó nhóm tác giả đẻ ra một khái niệm mới mang tên EL2N có định nghĩa như sau:

    Định nghĩa: Điểm EL2N của một mẫu đào tạo $(x, y)$ được định nghĩa là $\operatorname { E } \| p \left ( w _{ t }, x \right ) - y \|_ { 2 }$ Kết quả thử nghiệm của nhóm tác giả cho thấy rằng sự gần đúng này sẽ trở nên chính xác sau một vài epoch.

So sánh với forgetting scores

    Toneva và cộng sự trong bài báo An Empirical Study of Example Forgetting during Deep Neural Network Learning xác định “forgetting event” (forgetting event) cho một mẫu huấn luyện để trở thành một điểm trong huấn luyện khi bộ phân loại chuyển từ quyết định phân loại chính xác sang quyết định phân loại không chính xác. Họ xác định điểm số quên gần đúng cho mỗi mẫu đào tạo là số lần trong quá trình đào tạo khi nó được đưa vào một minibatch và trải qua một forgetting event. Nhóm tác giả này cũng chứng minh rằng các mẫu có forgetting score thấp có thể được bỏ qua hoàn toàn trong quá trình đào tạo mà không có bất kỳ ảnh hưởng đáng chú ý nào đến độ chính xác của dự đoán đã học. Như trong bổ đề được trình bày ở trên, nhóm tác giả đã giới hạn lượng đóng góp của một mẫu huấn luyện vào việc giảm sự mất mát của bất kỳ mẫu nào khác qua một bước gradient duy nhất. Do $\psi _{ t } \left ( \cdot \right )$ phụ thuộc vào thời gian, chúng rất phức tạp khi mở rộng phân tích thành nhiều bước. Tuy nhiên, thật thú vị khi xem xét một trường hợp khi $\psi_ { t } \left ( \cdot \right ) = \psi \left ( \cdot \right )$ cho tất cả $x_i$ trong tập huấn luyện, và $K = 1$. Sau đó tính tổng các ràng buộc trong bôt đề ở trên với mức độ ảnh hưởng của một mẫu $(x_j, y_j)$ đến đầu ra logit tại một điểm tùy ý tại mỗi thời điểm $t \in {1, .., T}$, chúng ta thu được điểm phụ thuộc vào $\| \psi \left ( x _{ j } \right ) | | \sum_ { t } \left ( p _{ t } \left ( x_ { j } \right ) - y _{ j } \right ) |$ Với hai mẫu khác nhau $(x, y)$ và $\left ( x ^ { \prime }, y ^ { \prime } \right )$ có $\| \psi \left ( x ^ { \prime } \right ) \| \approx \| \psi \left ( x \right ) \|$,ta thấy rằng mẫu được học nhanh hơn và duy trì lỗi nhỏ trong thời gian đào tạo sẽ có điểm GraNd nhỏ hơn trung bình trong suốt quá trình đào tạo. Lưu ý rằng $| \left ( p_ { t } \left ( x _{ j } \right ) - y_ { j } \right ) |$, nếu được rescaled, là giới hạn trên khi khoảng lỗi 0–1, và do đó $\sum _{ t } | \left ( p_ { t } \left ( x _{ j } \right ) - y_ { j } \right ) |$ giới hạn trên số forgetting event trong quá trình đào tạo (sau khi thay đổi tỷ lệ). Trong thiết lập đơn giản này, một mẫu có số lượng forgetting event cao cũng sẽ có điểm GraNd cao.

Đánh giá thực nghiệm về điểm GraNd và EL2N thông qua việc cắt tỉa dữ liệu

    Trong phần này, nhóm tác giả đánh giá các điểm số GraNd và EL2N theo kinh nghiệm và xác minh rằng chúng xác định các mẫu dữ liệu quan trọng để tổng quát hóa. Các mạng được đào tạo trên tập hợp con của dữ liệu có điểm số cao đạt được mức độ chính xác của bài kiểm tra tương đương với việc đào tạo trên tập dữ liệu đầy đủ và có khả năng cạnh tranh với các phương pháp cắt tỉa dữ liệu hiện đại khác. Có lẽ đáng chú ý nhất, những điểm số này có hiệu quả ngay cả khi được tính toán sớm trong quá trình đào tạo và hoạt động tốt hơn đáng kể so với đường cơ sở ngẫu nhiên, ngay cả khi khởi tạo.

    Thí nghiệm cắt tỉa dữ liệu: Nhóm tác giả đào tạo mạng nơ-ron phức hợp có độ sâu khác nhau – ResNet18 và ResNet50 – trên bộ dữ liệu tiêu chuẩn có độ khó khác nhau – CIFAR-10, CIFAR-100 và CINIC-10. Tất cả các điểm số được tính bằng cách lấy điểm trung bình từ mười lần chạy huấn luyện độc lập. Sau khi tính toán điểm số và chọn một tập hợp con huấn luyện, độ chính xác của bài kiểm tra cuối cùng được thu được bằng các mạng đào tạo lại từ các lần khởi tạo ngẫu nhiên chỉ trên tập hợp con đã chọn. Đối với mỗi thử nghiệm, nhóm tác giả báo cáo giá trị trung bình của bốn lần chạy độc lập và biểu thị sự thay đổi trên các lần chạy bằng cách tô bóng vùng trải dài từ phân vị thứ 16 đến 84 của độ chính xác thu được.

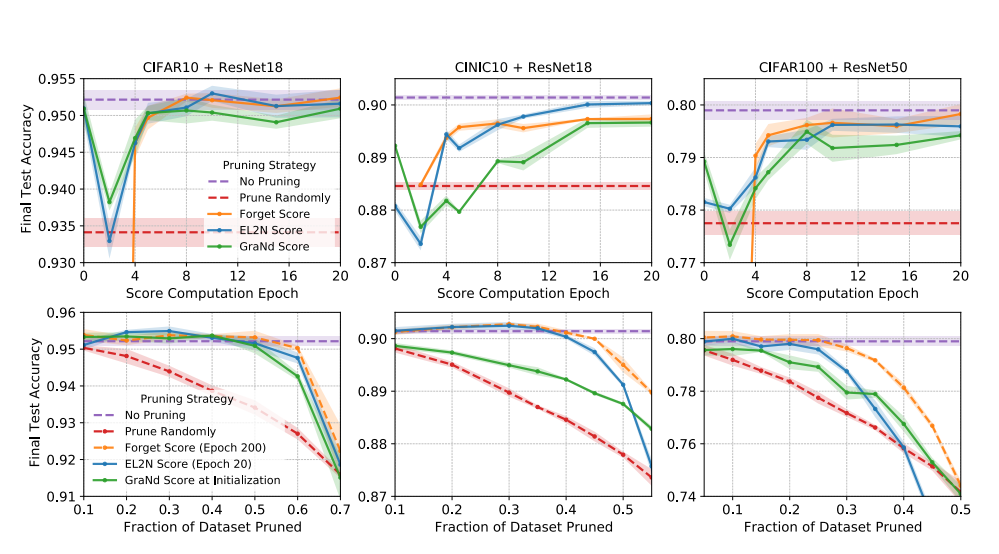
    Các cột tương ứng với ba kết hợp mạng và tập dữ liệu khác nhau (được gắn nhãn ở trên cùng). Hàng đầu tiên: Độ chính xác của bài kiểm tra cuối cùng đạt được khi đào tạo trên một tập hợp con dữ liệu đào tạo bao gồm các mẫu có điểm số quên tối đa, EL2N và GraNd được tính toán vào các thời điểm khác nhau trong quá trình đào tạo. Các tập con có kích thước cố định được sử dụng: mạng được huấn luyện dựa trên 50% dữ liệu huấn luyện cho CIFAR10, 60% cho CINIC-10 và 75% cho CIFAR-100. Hàng thứ hai: Độ chính xác của thử nghiệm cuối cùng đạt được bằng cách đào tạo sau khi các phần khác nhau của tập dữ liệu được lược bớt. Ở đây nhóm tác giả so sánh forgetting score khi kết thúc đào tạo, điểm EL2N sớm khi đào tạo (ở epoch 20) và điểm GraNd khi khởi chạy. Trong mỗi trường hợp, các mẫu có điểm thấp nhất sẽ được lược bớt khi khởi tạo. Trong tất cả các thử nghiệm, độ chính xác đạt được bằng cách đào tạo trên tập dữ liệu đầy đủ và trên một tập hợp con ngẫu nhiên có kích thước tương ứng được sử dụng làm baseline. Cũng trong hình trên, nhóm tác giả hiển thị kết quả của hai nhóm thử nghiệm (trên và dưới) trên ba kết hợp mạng và tập dữ liệu khác nhau. Thí nghiệm đầu tiên đặt câu hỏi, những người hay quên trong quá trình luyện tập sớm, điểm GraNd và EL2N có hiệu quả như thế nào trong việc xác định các mẫu quan trọng đối với sự tổng quát hóa? nhóm tác giả so sánh độ chính xác của bài kiểm tra cuối cùng từ việc đào tạo trên các tập hợp con có kích thước cố định nhưng được lược bớt dựa trên điểm số được tính ở các thời điểm khác nhau trong quá trình đào tạo. Thử nghiệm thứ hai so sánh cách GraNd đạt điểm khi khởi tạo, điểm EL2N sớm khi đào tạo và forgetting score khi kết thúc đào tạo thương lượng sự cân bằng giữa hiệu suất tổng quát hóa và kích thước tập hợp đào tạo. Các tập huấn luyện được xây dựng bằng cách cắt bớt các phần khác nhau của các mẫu có điểm thấp nhất. Trong tất cả các mẫu, đào tạo về tập dữ liệu đầy đủ và một tập hợp con ngẫu nhiên có kích thước tương ứng được sử dụng làm đường cơ sở. nhóm tác giả thực hiện các quan sát sau đây.

    Tỉa khi khởi tạo. Trong tất cả các cài đặt, điểm GraNd có thể được sử dụng để chọn một tập hợp con đào tạo khi khởi tạo đạt được độ chính xác của bài kiểm tra tốt hơn đáng kể so với ngẫu nhiên và trong một số trường hợp, có thể so sánh với đào tạo trên tất cả dữ liệu. Điều này là đáng chú ý vì GraNd chỉ chứa thông tin về tiêu chuẩn gradient khi khởi tạo, được tính trung bình qua các lần khởi tạo. Điều này cho thấy rằng hình học của phân bố huấn luyện do một mạng ngẫu nhiên tạo ra chứa một lượng thông tin đáng ngạc nhiên về cấu trúc của bài toán phân loại. Điểm EL2N, chỉ chứa thông tin về lỗi, không hiệu quả nhất quán khi khởi tạo và forgetting score, yêu cầu đếm các sự kiện quên trong quá trình đào tạo, không được xác định khi khởi tạo.

    Cắt tỉa sớm trong quá trình đào tạo. Nhóm tác giả nhận thấy rằng, chỉ sau một vài epoch đào tạo, điểm EL2N cực kỳ hiệu quả trong việc xác định các mẫu quan trọng để khái quát hóa. Đối với một loạt các cấp độ cắt tỉa trung gian, đào tạo trên điểm cao nhất thực hiện ngang bằng hoặc tốt hơn đào tạo trên tập dữ liệu đầy đủ. Ngay cả ở các cấp độ cắt tỉa cao hơn, điểm EL2N được tính bằng cách sử dụng thông tin địa phương sớm trong quá trình đào tạo cũng có khả năng cạnh tranh với forgetting score tích hợp thông tin trên quỹ đạo đào tạo. Điều này cho thấy rằng vectơ lỗi trung bình một vài epoch trong quá trình huấn luyện có thể xác định các mẫu mà mạng sử dụng nhiều để định hình ranh giới quyết định trong suốt quá trình huấn luyện.

    Điều thú vị là ở mức độ cắt tỉa cực cao với điểm EL2N hoặc GraNd, nhóm tác giả quan sát thấy hiệu suất giảm mạnh. Nhóm tác giả giả thuyết rằng điều này là do ở mức độ cắt tỉa cao, việc sử dụng điểm GraNd hoặc EL2N dẫn đến mức độ bao phủ của phân phối dữ liệu không tốt. Bằng cách chỉ tập trung vào các mẫu lỗi cao nhất, có khả năng là toàn bộ quần thể con có kích thước đáng kể có trong dữ liệu thử nghiệm hiện bị loại khỏi tập huấn luyện. Việc chỉ fit với một số lượng nhỏ các mẫu rất khó và không giữ đủ tính đa dạng cho các mô hình huấn luyện với lỗi kiểm tra tốt.

    Thuộc tính của dữ liệu. Hai kết quả gợi ý rằng xếp hạng của các mẫu quan trọng được tạo ra bởi điểm số EL2N và GraNd là một thuộc tính của tập dữ liệu và không cụ thể cho một mạng. Đầu tiên, thông qua thực nhiệm, nhóm tác giả chỉ ra rằng ResNet18 và ResNet50 được đào tạo trên CIFAR-10 có các đường cong hiệu suất tương tự và lượng dữ liệu tương tự có thể được lược bớt, mặc dù ResNet50 là một mạng sâu hơn nhiều với nhiều tham số hơn. Ngoài ra, trong một phân tích về độ nhạy của các phương pháp tính điểm đối với các siêu tham số, nhóm tác giả nhận thấy rằng các điểm được tính trên một mạng đơn lẻ không hoạt động tốt bằng các điểm được tính trung bình trên các mạng. Nhóm tác giả đưa ra giả thuyết rằng việc tính trung bình các chỉ tiêu độ dốc hoặc sai số qua nhiều lần khởi tạo hoặc quỹ đạo đào tạo loại bỏ sự phụ thuộc vào các trọng lượng cụ thể, cho phép chắt lọc chính xác hơn các thuộc tính của tập dữ liệu.

    Trong các thử nghiệm sau đây, nhóm tác giả tập trung vào điểm EL2N được tính toán sớm trong quá trình đào tạo, vì chúng dường như xác định chính xác hơn các mẫu quan trọng.

Xác định các mẫu nhiễu

    Trong phần trước, nhóm tác giả đã nghiên cứu tác động của việc lưu giữ các mẫu có điểm số cao nhất và nhận thấy rằng nhóm tác giả chỉ có thể đào tạo trên 50% các mẫu hàng đầu theo điểm số mà không giảm độ chính xác (CIFAR-10). Bản chất của quần thể con của các mẫu cho phép chúng ta đạt được độ chính xác cao là gì? Một giả thuyết cho rằng các mẫu có điểm cao nhất là những mẫu quan trọng nhất để đạt được bộ phân loại chính xác. Trong phần này, nhóm tác giả bác bỏ giả thuyết này và chứng minh vai trò của nhiễu nhãn.

    Để kiểm tra xem các mẫu đạt điểm cao nhất có quan trọng về chi phí để đạt được độ chính xác cao hay không, trước tiên nhóm tác giả sắp xếp các mẫu theo chiều tăng dần của điểm EL2N được tính sau một số lượng nhỏ training epoch. Sau đó, nhóm tác giả thực hiện phân tích cửa sổ trượt bằng cách đào tạo trên một tập hợp con các mẫu có điểm trong cửa sổ từ phân vị $f$ đến phân vị $f + P$, luôn giữ $P$ dữ liệu nhưng trượt lên $f$. Khi cửa sổ này trượt đến phần trăm cao hơn, hiệu suất sẽ tăng lên, ngoại trừ khi cửa sổ bao gồm các mẫu có điểm rất cao như hình bên dưới. Thật vậy, cửa sổ trượt tối ưu thực sự loại trừ khoảng 500 mẫu đào tạo đạt điểm cao nhất. Những ảnh hưởng này bị giảm bớt trong chế độ tỉa thưa.

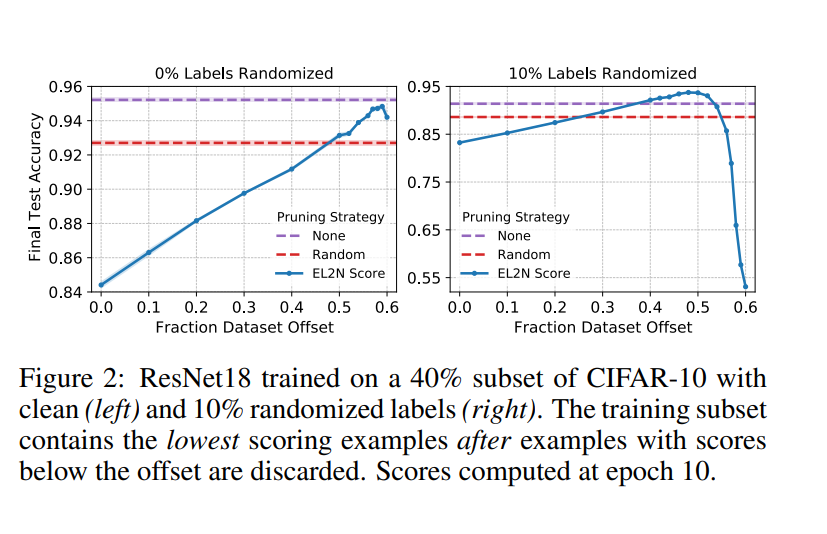
    Trước khi nhóm tác giả phân tích những kết quả này, trước tiên nhóm tác giả đặt chúng vào một bối cảnh rộng hơn, nơi nhóm tác giả cũng thay đổi lượng nhiễu trong phân phối nhãn bên dưới. Nhóm tác giả lặp lại thử nghiệm được nêu ở trên, nhưng làm hỏng ngẫu nhiên $K$ nhãn, thay thế chúng bằng một nhãn ngẫu nhiên, phản ánh giao thức được phổ biến bởi Zhang và cộng sự trong Understanding deep learning requires rethinking generalization. Hình trên cũng cho thấy cho thấy rằng với sự gia tăng của việc làm hỏng ngẫu nhiên nhãn, cửa sổ tối ưu sẽ thay đổi và loại trừ số lượng mẫu cao hơn. Do đó, hiệu ứng mà chúng ta thấy trong trường hợp không có nhiễu dường như được phóng đại khi có nhiễu nhãn.

    Những phát hiện này có một số ý nghĩa. Hàm ý rõ ràng nhất là việc huấn luyện chỉ với các mẫu có điểm cao nhất có thể không tối ưu, đặc biệt là khi có nhiễu nhãn. Khi phân bố có tỷ lệ lỗi Bayes thấp, chỉ sử dụng các mẫu có điểm cao nhất mới mang lại kết quả tối ưu. Tuy nhiên, nếu không có tập validate, ta nên thận trọng trong việc loại trừ các mẫu điểm cao. Feldman [14] thảo luận về việc ghi nhớ trong thiết lập nhãn nhiễu và đưa ra các điều kiện mà theo đó người ta nên ghi nhớ để không phân loại sai các mẫu singleton (mẫu trong dữ liệu đào tạo là đại diện duy nhất của một quần thể con). mẫu, nếu quần thể con xuất hiện với tần suất $\Omega (1/ N)$, ghi nhớ các mẫu như vậy có thể cải thiện khả năng khái quát hóa. Trên thực tế, nhóm tác giả có thể không biết liệu dữ liệu của mình có phù hợp với các điều kiện này hay không. Tuy nhiên, phân tích của nhóm tác giả trong hình trên gợi ý một phương pháp đơn giản và mạnh mẽ để cắt bớt dữ liệu để có hiệu suất tối ưu bằng cách tối ưu hóa chỉ hai siêu tham số của cửa sổ trượt bằng cách sử dụng bộ xác thực.

Optimization landscape và training dynamics

    Mình không biết dịch 2 từ trên kiểu gì :v

    Động lực của đào tạo mạng nơron trong giới hạn chiều rộng vô hạn hiện đã được hiểu rõ: để có tỷ lệ thích hợp về tốc độ học và trọng số ban đầu, mạng nơron hoạt động giống như một mô hình tuyến tính trong đó dữ liệu được biến đổi bởi Neural Tangent Kernel (NTK) khi khởi tạo, được định nghĩa là sản phẩm của Jacobian của các logits khi khởi tạo. Trong giới hạn, đào tạo mạng nơ-ron thực hiện kernel regression với NTK cố định là kernel.

    Tuy nhiên, mạng nơ-ron hữu hạn hoạt động tốt hơn giới hạn băng thông vô hạn của chúng và có các động lực khác nhau ở giai đoạn đầu đào tạo. Trên thực tế, thay vì không đổi, NTK phụ thuộc vào dữ liệu (data-dependent NTK), được xác định bởi Fort và các cộng sự trong Deep learning versus kernel learning: an empirical study of loss landscape geometry and the time evolution of the Neural Tangent Kernel là ma trận Gram của logit Jacobian, phát triển với tốc độ cao trong giai đoạn đầu của quá trình huấn luyện. Sau đó, vào khoảng thời gian bắt đầu kết nối chế độ tuyến tính, vận tốc NTK ổn định ở một giá trị nhỏ hơn và gần như không đổi trong phần còn lại của thời gian đào tạo tốc độ học tập cao.

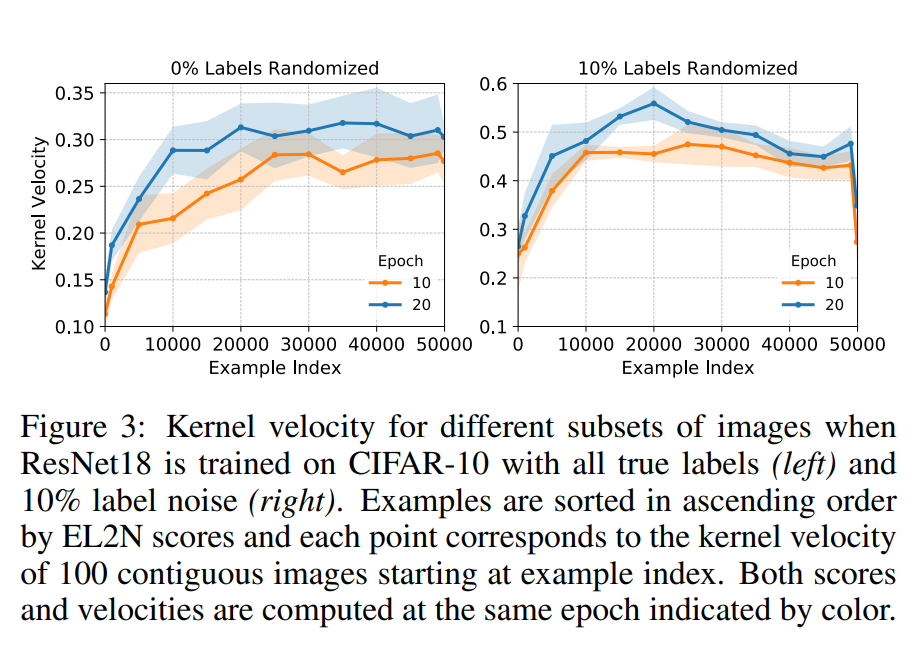
    Ở đây, nhóm tác giả tìm hiểu những mẫu đào tạo nào đóng góp vào sự phát triển của ma trận gram NTK. Để tính gần đúng theo kinh nghiệm vận tốc của ma trận con NTK tương ứng với một tập hợp con các hình ảnh theo một cách bất biến tỷ lệ, nhóm tác giả làm theo bài báo Deep learning versus kernel learning mà theo đó, họ tính khoảng cách cosin giữa hai ma trận gram NTK trên tập con đã cho, một ma trận được tính ở epoch $t$ và một ma trận khác ở epoch $t + 1$, là một epoch sau đó. Nhóm tác giả xem xét các ma trận con có kích thước cố định, được hình thành bởi các mẫu có điểm EL2N liền kề. Hình sau cho thấy điểm EL2N cao hơn dẫn đến vận tốc cao hơn. Mối quan hệ này không bị ảnh hưởng bởi thời gian mà cả hai được tính toán.

    Điều thú vị là tốc độ hạt nhân giảm mạnh đối với các mẫu có điểm rất cao khi nhiễu nhãn được đưa vào. Trong phần trước, nhóm tác giả đã chỉ ra rằng việc bỏ các mẫu này sẽ tăng độ chính xác của dự đoán cuối cùng. Nhóm tác giả đưa ra giả thuyết rằng, trong khi tốc độ hạt nhân cao hơn đối với các mẫu khó hơn mà mô hình đang tích cực cố gắng để phù hợp, thì tốc độ hạt nhân giảm xuống đối với các mẫu có điểm cao nhất có thể quá khó học, có lẽ vì chúng là mẫu không đại diện hoặc chúng có nhãn nhiễu.

Kết nối với Linear Mode Connectivity

    Bây giờ chúng ta kiểm tra cách xếp hạng của các mẫu bằng EL2N kết nối với hình học của bề mặt hàm mất mát. Đặc biệt, Frankle và các cộng sự trong Linear mode connectivity and the lottery ticket hypothesis đã nghiên cứu ảnh hưởng của tính ngẫu nhiên của minibatch lên quỹ đạo huấn luyện, tập trung vào việc xác định điểm trong việc huấn luyện khi hai mạng, bắt đầu từ cùng trọng số, nhưng được huấn luyện với các minibatch độc lập, hội tụ về cùng một mode "kết nối tuyến tính". Họ nhận thấy rằng, đối với các bộ dữ liệu thị lực tiêu chuẩn, sự khởi đầu của “kết nối chế độ tuyến tính” (LMC, linear mode connectivity) này xảy ra sớm trong quá trình đào tạo.

    Chính xác hơn, hãy để $w_1, w_2 ,. . . , w_T$ là quỹ đạo huấn luyện của mạng mẹ, cố định thời gian spawning time $t^∗$, và đặt $v_{t^∗}, v_{t^∗ + 1}, v_{t^∗ + 2} ,. . . , v_T$ là một quỹ đạo đào tạo độc lập (tức là với các nhóm nhỏ độc lập), bắt đầu tại $v_{t^∗} = w_{t^∗}$. Nhóm tác giả gọi gọi $v_T$ là mạng con và $v_{t^∗}, v_{t^∗ + 1} ,. . .$ quỹ đạo con. error barrier (huấn luyện) giữa hai trọng số $w$ và $w^\prime$, được ký hiệu là $err (w, w^\prime; S)$, là độ lệch lớn nhất của bề mặt lỗi huấn luyện $\hat{R}_S (\cdot)$ trên line connecting the empirical risk (đường nối rủi ro thực nghiệm ?? ??) tại $w$ và $w^\prime$ . Đó là,

    $$\operatorname { e r r } \left ( w, w ^ { \prime } ; S \right ) = \sup _ { \alpha \in \left [ 0, 1 \right ] } \{ \hat { R } _ { S } \left ( \alpha w + \left ( 1 - \alpha \right ) w ^ { \prime } \right ) - \alpha \hat { R } _ { S } \left ( w \right ) - \left ( 1 - \alpha \right ) \hat { R } _ { S } \left ( w ^ { \prime } \right ) \}.$$

    Sau đó, nhóm tác giả xác định error barrier trung bình (huấn luyện), sinh ra tại $t^∗$, tại thời điểm $t$, với $t^∗ ≤ t ≤ T$, được ký hiệu là $err_t^{t^*} (S)$, là error barrier dự kiến giữa $w_t$ và $v_t$ trên dữ liệu $S$. Đó là:

    $$\operatorname { e r t } _ { t } ^ { t ^ { * } } \left ( S ^ { \prime } \right ) = \operatorname{E}_{w_{t^* +1:t}, v_{t^* + 1, t}} [\operatorname{err} (w_t, v_t; S)]$$

    Trong đó kỳ vọng được thực hiện dựa trên tính ngẫu nhiên trong quỹ đạo của $w$ và $v$ sau $t^∗$ do sự lựa chọn minibatch, có điều kiện đối với quỹ đạo ban đầu đi lên trong thời gian $t^∗$. (Lưu ý rằng, khi kết thúc quá trình huấn luyện $t = T$, giá trị tối cao trong $err (w_T, v_T; S)$ thường đạt được gần $\alpha = 1/2$ và vì vậy đây là một phép gần đúng với chi phí thấp được sử dụng trong thực tế.) “Thời điểm bắt đầu” của kết nối chế độ tuyến tính là spawning time $t^*$ tại thời điểm đó $err^{t^∗}_T (S) ≈ 0$, trong đó $S$ là toàn bộ tập huấn luyện. Trong công việc của mình, thay vào đó, nhóm tác giả tính toán hàng rào lỗi trên các tập con của tập huấn luyện, điều này cho phép nhóm tác giả so sánh các training dynamics và chế độ huấn luyện trên các quần thể con.

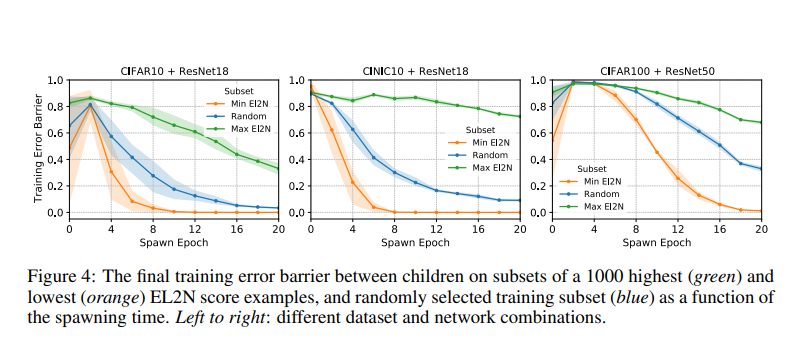
    Trong hình trên, nhóm tác giả đo mean error barrier $err^{t^∗}_T (S^\prime)$ dưới dạng hàm của spawning time $t^∗$, trong trường hợp $S^\prime$ 0 là: 1) tập hợp các mẫu đào tạo có điểm nhỏ nhất, 2) tập hợp các mẫu đào tạo có điểm lớn nhất, hoặc 3) một tập hợp con ngẫu nhiên của các mẫu đào tạo. Nhóm tác giả nhận thấy rằng error barrier giảm xuống gần bằng 0 rất nhanh đối với các mẫu có điểm EL2N thấp và vẫn ở mức cao đối với các mẫu có điểm cao. Những phát hiện này cho thấy rằng Bề mặt hàm lỗi bắt nguồn từ các tập hợp con hạn chế của các mẫu có EL2N thấp và cao hoạt động rất khác nhau. Bề mặt hàm lỗi bắt nguồn từ các tập hợp con dễ dàng của các mẫu có điểm thấp là khá bằng phẳng, theo nghĩa là error barrier giữa các con như một hàm của thời gian đẻ trứng nhanh chóng giảm đi. Mặt khác, Bề mặt hàm lỗi bắt nguồn từ các tập hợp con khó hơn của các mẫu có điểm số cao hơn là khó khăn hơn, với các error barrier cao hơn và tồn tại lâu hơn trong thời gian xuất hiện. Hơn nữa, kết quả này phù hợp với kết quả được trình bày trong phần ngay trước đó, cho thấy rằng hầu hết việc học tập xảy ra trong các mẫu về điểm EL2N cao.

Tổng kết

    Sau gần nửa tiếng đọc một tỷ công thức toán ở trên, ta có thể tóm gọn lại các đóng góp của nhóm tác giả bao gồm:

•     Tìm cách xác định mức độ trung bình của mỗi mẫu đào tạo ảnh hưởng đến việc giảm tổn thất của các mẫu khác và từ điểm bắt đầu đó và từ đó thu được 2 điểm, đó là định mức gradient (GraNd) và định mức sai số (EL2N) ràng buộc hoặc gần đúng ảnh hưởng này, với điểm số cao hơn cho thấy ảnh hưởng tiềm năng cao hơn.

•     Cung cấp đưa ra giả thuyết và chứng minh rằng các mẫu có điểm số cao hơn có xu hướng khó học hơn, có nghĩa là chúng thường bị lãng quên hơn trong toàn bộ quá trình đào tạo.

•     Cung cấp đưa ra giả thuyết và chứng minh rằng các mẫu cho điểm cao nhất có xu hướng hoặc là các ngoại lệ không mang tính đại diện của một lớp, có nền không chuẩn hoặc các góc kỳ lạ, có thể bị nhiễu nhãn hoặc khó khăn.

•     Cung cấp đưa ra giả thuyết và chứng minh rằng tập hợp con các mẫu có điểm số cao hơn (thấp hơn) góp phần vào cảnh quan mất mát thô hơn (mượt mà hơn).

    Nhìn chung, sự phân rã của cả loss landscape geometry và learning dynamics thành những đóng góp khác nhau từ các loại mẫu khác nhau tạo thành một phương pháp luận mới thú vị để phân tích các tác vụ Deep Learning. Hiểu biết sâu hơn về vai trò khác biệt giữa các tập hợp con các mẫu khác nhau có thể hỗ trợ không chỉ trong việc lược bớt dữ liệu mà còn hỗ trợ trong việc thiết kế phương pháp huấn luyện, active learning, federated learning, vân vân và mây mây. Tuy vậy thì kết quả chưa được cụ thể cho lắm, bởi vậy tính hiệu quả của chúng khó có thể được xác định rõ ràng. Nói tóm lại, đây vẫn là một bài báo khá đáng để đọc, chi tiết về nhận xét mọi người có thể đọc thêm trên https://openreview.net/forum?id=Uj7pF-D-YvT. Bài viết của mình đến đây là kết thúc, cảm ơn mọi người đã dành (rất nhiều) thời gian đọc.