I. Lời mở đầu

Ngăn xếp (Stack) và Hàng đợi (Queue) là hai trong số những cấu trúc dữ liệu cực kỳ quan trọng, được sử dụng thường xuyên trong thiết kế thuật toán. Chính máy tính cũng sử dụng nhiều ứng dụng của ngăn xếp (chẳng hạn như việc quản lý bộ nhớ trong khi thi hành chương trình, hay lưu trữ các lời gọi đệ quy,...). Về bản chất, ngăn xếp và hàng đợi cũng giống như mảng, chúng là một tập hợp các phần tử cùng kiểu dữ liệu, nhưng được lưu trữ có tính thứ tự.

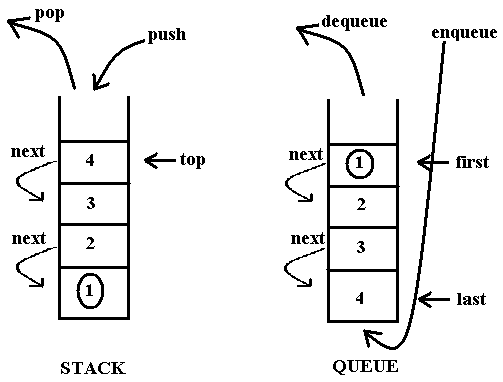
Trong chuyên đề này, tôi sẽ giới thiệu tới các bạn về hoạt động của ngăn xếp và hàng đợi, cũng như cách cài đặt chúng thật đơn giản. Ngoài ra, chúng ta cũng sẽ cùng xem xét một số bài toán ứng dụng hai cấu trúc dữ liệu này để hiểu rõ hơn về cách sử dụng chúng.

Để cho đơn giản, ta sẽ thống nhất gọi $\text{type}$ là kiểu dữ liệu của các phần tử trong ngăn xếp và hàng đợi. Khi cài đặt cụ thể, $\text{type}$ có thể là kiểu số, kiểu chữ hay thậm chí là một kiểu cấu trúc do người dùng tự định nghĩa.

II. Ngăn xếp (Stack)

1. Khái niệm

Ngăn xếp là một kiểu danh sách mà việc bổ sung một phần tử và xóa một phần tử được thực hiện ở cuối danh sách.

Hãy hình dung ngăn xếp giống như một chồng đĩa. Các bạn muốn thêm một chiếc đĩa vào thì phải đặt nó lên đỉnh của chồng đĩa (phía cuối), và muốn lấy một chiếc đĩa ra thì cũng phải lấy từ trên xuống.

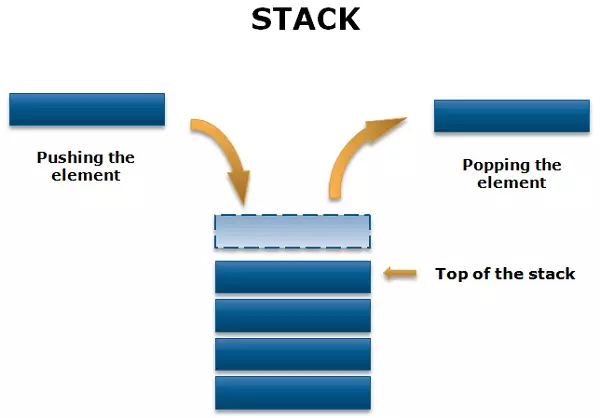
Phần tử ở đỉnh ngăn xếp (cuối danh sách) được gọi là phần tử top của ngăn xếp. Nguyên tắc thêm - xóa phần tử như trên được gọi là "vào sau ra trước", do đó ngăn xếp còn có tên gọi khác là danh sách kiểu LIFO (Last In First Out). Có $6$ thao tác cơ bản ngăn xếp cung cấp:

$\text{init}$ : Khởi tạo ngăn xếp rỗng.
$\text{is\_empty}$ : Kiểm tra xem ngăn xếp có rỗng không.
$\text{is\_full}$ : Kiểm tra xem ngăn xếp có bị đầy (tràn) hay không.
$\text{get\_top}$ : Trả về phần tử ở đỉnh ngăn xếp.
$\text{push}$ : Thêm một phần tử vào ngăn xếp.
$\text{pop}$ : Lấy ra phần tử ở đỉnh ngăn xếp.

Có hai cách để biểu diễn ngăn xếp là sử dụng mảng hoặc danh sách liên kết, tuy nhiên do những ngôn ngữ hiện đại như C++ và Python đã không còn ưu tiên sử dụng danh sách liên kết, cũng như đã cài đặt sẵn stack và queue, nên ở đây tôi chỉ phân tích sơ qua cách cài đặt bằng mảng để bạn đọc hiểu về cơ chế của cấu trúc dữ liệu này.

2. Biểu diễn ngăn xếp bằng mảng

Để biểu diễn ngăn xếp, ta sử dụng một mảng $\text{elements}$ để lưu các phần tử của ngăn xếp, phần tử cuối cùng của mảng chính là phần tử top của ngăn xếp. Containers vector trong C++ và list trong Python dễ dàng kiểm soát điều này.

Tuy nhiên, vì vector trong C++ và list trong Python thường được cấp phát bộ nhớ rất lớn trong máy tính, nên việc kiểm tra ngăn xếp có bị đầy hay không là không cần thiết. Vì vậy, ở đây tôi sẽ không cài đặt thao tác $\text{is\_full}$ .

Ngôn ngữ C++:

#include <iostream>
#include <vector>

using namespace std;

// Tạo một cấu trúc ngăn xếp là một vector có kiểu phần tử type.
typedef vector < {type} > stack_type;

// Khởi tạo ngăn xếp rỗng.
void create_stack(stack_type &st)
{
    st.resize(0);    
}

// Kiểm tra ngăn xếp có rỗng không.
bool is_empty(stack_type &st)
{
    return st.empty();
}

// Trả ra phần tử ở đỉnh ngăn xếp nếu tồn tại.
{type} get_top(stack_type &st)
{
    if (!st.empty())
        return st.elements.back();
    else
        {Báo_lỗi_ngăn_xếp_rỗng};
}

// Đẩy một phần tử vào ngăn xếp.
void push(stack_type &st, {type} x)
{
    stack.push_back(x);
}

// Lấy ra phần tử ở đỉnh ngăn xếp.
void pop(stack_type &st)
{
    return st.pop_back();
}

Ngôn ngữ Python:

# Khởi tạo ngăn xếp rỗng.
def create_stack(st):
    st = []

# Kiểm tra ngăn xếp có rỗng không.
def is_empty(st):
    return len(st) == 0

# Trả về phần tử ở đỉnh ngăn xếp.
def get_top(st):
    if len(st) > 0:
        return st[-1]
    else:
        {Báo_lỗi_ngăn_xếp_rỗng}

# Thêm một phần tử vào ngăn xếp.
def push(st, x):
    st.append(x)

# Xóa phần tử ở đỉnh ngăn xếp.
def pop(st):
    st.pop()

III. Hàng đợi (Queue)

1. Khái niệm

Giống như tên gọi của mình, hàng đợi là một cấu trúc dữ liệu biểu diễn một danh sách các phần tử đứng trong "hàng chờ" được xử lý. Trong cấu trúc dữ liệu này, việc bổ sung một phần tử được thực hiện ở cuối danh sách, còn việc loại bỏ một phần tử được thực hiện ở đầu danh sách.

Có thể tưởng tượng hàng đợi giống như một hàng người xếp hàng chờ mua vé, ai đến trước được mua trước và rời khỏi hàng, còn những người đến sau sẽ bổ sung vào cuối hàng. Vì nguyên tắc "vào trước ra trước" như vậy nên hàng đợi còn được gọi là danh sách kiểu FIFO (First In First Out).

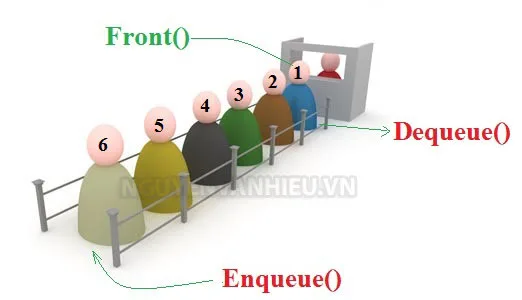
Phần tử ở đầu hàng đợi sẽ gọi là phần tử front, còn phần tử ở cuối hàng đợi gọi là phần tử rear. Tương tự như ngăn xếp, có $6$ thao tác cơ bản trên hàng đợi:

$\text{init}$ : Khởi tạo một hàng đợi rỗng.
$\text{is\_empty}$ : Kiểm tra hàng đợi có rỗng hay không.
$\text{is\_full}$ : Kiểm tra hàng đợi đã bị đầy chưa.
$\text{get\_front}$ : Trả về giá trị của phần tử ở đầu hàng đợi.
$\text{push}$ : Đẩy một phần tử vào cuối hàng đợi.
$\text{pop}$ : Loại bỏ một phần tử ở đầu hàng đợi.

2. Biểu diễn hàng đợi bằng mảng

Giống như ngăn xếp, ta sử dụng một mảng $\text{elements}$ để lưu các phần tử của hàng đợi. Tuy nhiên, ta phải sử dụng thêm một biến $\text{front}$ để kiểm soát vị trí của phần tử đầu tiên trong hàng đợi, còn phần tử cuối cùng thì vẫn là phần tử cuối của vector hoặc list. Tương tự như ngăn xếp, thao tác kiểm tra $\text{is\_full}$ cũng không cần thiết phải cài đặt.

Ý tưởng sẽ là, nếu như thêm một phần tử vào hàng đợi thì đẩy nó vào cuối danh sách $\text{elements},$ còn khi lấy ra một phần tử ở đầu hàng đợi thì ta tăng biến $\text{front}$ thêm $1$ đơn vị, như vậy coi như các phần tử từ vị trí $0$ tới vị trí $\text{front} - 1$ trên mảng là các phần tử đã bị loại đi.

Cả hai thành phần trên có thể gộp lại thành một cấu trúc $\text{queue\_type}$ trong C++, hoặc một class $\text{queue\_type}$ trong Python.

Ngôn ngữ C++:

#include <iostream>
#include <vector>

using namespace std;

const int max_size = {Kích_thước_cực_đại};

struct queue_type
{
    vector < {type} > elements;
    int front;
}

// Khởi tạo hàng đợi.
void init(queue_type &qu)
{
    qu.elements.resize(0);
    front = -1;
}

// Kiểm tra hàng đợi có rỗng không.
bool is_empty(queue_type &qu)
{
    return qu.front > qu.elements.size();
}

// Trả về phần tử ở đầu hàng đợi.
{type} get_front(queue_type qu)
{
    if (is_empty(qu))
        {Báo_lỗi_hàng_đợi_rỗng};
    else 
        return qu.elements[qu.front];
}

// Thêm một phần tử vào hàng đợi.
void push(queue_type &qu, {type} x)
{
    qu.elements.push_back(x);
}

// Xóa phần tử ở đầu hàng đợi.
void pop(queue_type &qu)
{
    if (is_empty(qu))
        {Báo_lỗi_hàng_đợi_rỗng};
    else 
        ++qu.front;
}

Ngôn ngữ Python:

# Tạo một class biểu diễn hàng đợi.
class queue_type:
    def __init__(sefl, elements, front):
        self.elements = elements
        self.front = front

# Khởi tạo hàng đợi rỗng.
def init(queue_type qu):
    qu.elements = []
    qu.front = -1

# Kiểm tra hàng đợi có rỗng không.
def is_empty(queue_type qu):
    return len(qu.elements) == 0

# Trả về phần tử ở đầu hàng đợi.
def get_front(queue_type qu):
    if len(qu.elements) == 0:
        {Báo_lỗi_hàng_đợi_rỗng}
    else:
        return qu.elements[qu.front]

# Thêm một phần tử vào hàng đợi.
def push(queue_type qu, x):
    qu.elements.append(x)

# Xóa đi phần tử ở đầu hàng đợi.
def pop(queue_type qu):
    if is_empty(qu):
        {Báo_lỗi_hàng_đợi_rỗng}
    else:
        ++qu.front

IV. Sử dụng `stack` và `queue` dựng sẵn trong C++ và Python

Trên thực tế, trong các ngôn ngữ lập trình bậc trung và bậc cao đều đã xây dựng sẵn hai cấu trúc dữ liệu ngăn xếp và hàng đợi để tiết kiệm thời gian cho lập trình viên. Trong các kì thi lập trình, hay trong công việc, chúng ta cũng không cần thiết phải cài đặt thủ công hai cấu trúc dữ liệu này mà chỉ cần sử dụng sẵn là được.

1. Trong thư viện STL C++

Thư viện template chuẩn C++ (STL) cung cấp sẵn hai container stack và queue biểu diễn hai cấu trúc dữ liệu ngăn xếp và hàng đợi. Để sử dụng, các bạn cần khai báo thư viện stack và queue cùng với không gian tên std. Sau đó, cú pháp khai báo hàng đợi và ngăn xếp như sau:

stack < {Kiểu_phần_tử} > {Tên_biến_ngăn_xếp};
queue < {Kiểu_phần_tử} > {Tên_biến_hàng_đợi};

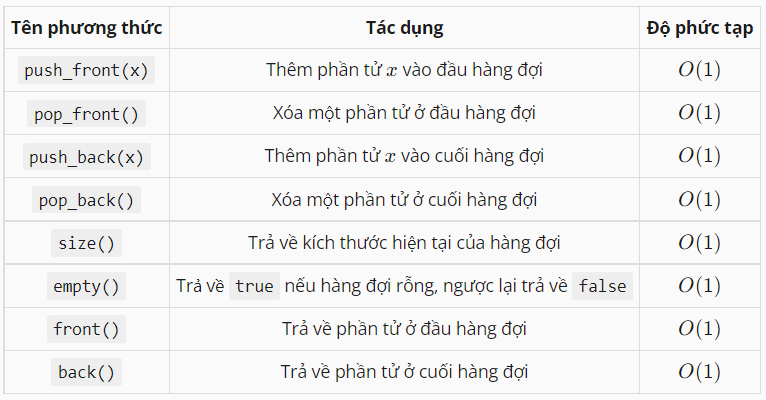
Các hàm dựng sẵn của hai containers này được cho ở bảng dưới đây. Để sử dụng các hàm đó, các bạn sử dụng cú pháp: {Tên_biến}.{Tên_hàm}.

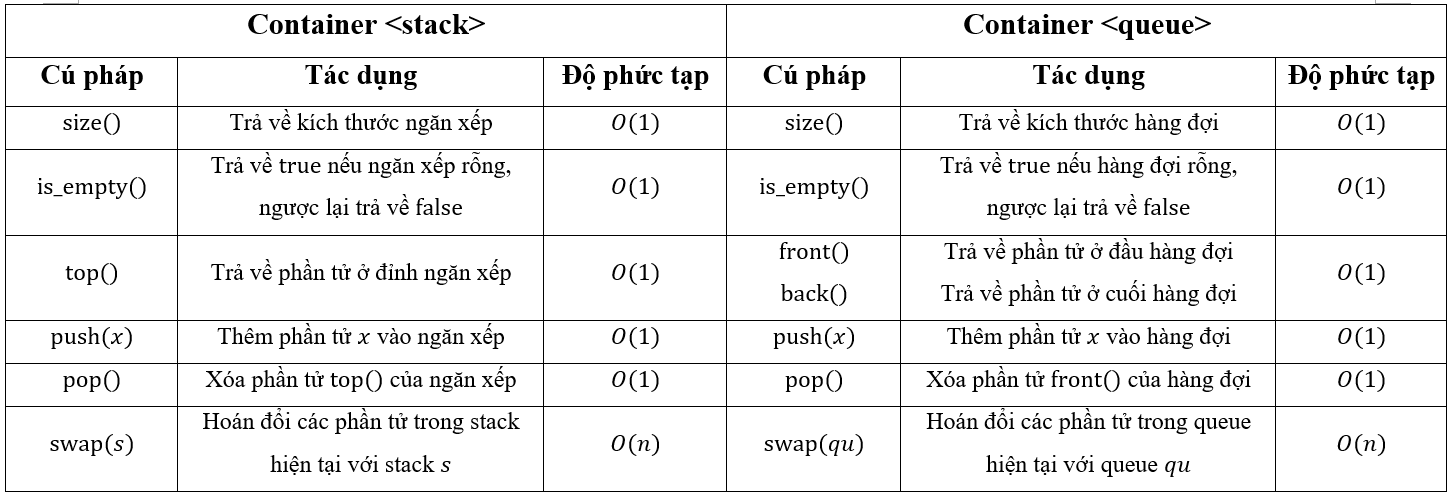
Ngoài ra trong STL C++ cũng hỗ trợ một container nữa là deque (hàng đợi hai đầu), là sự kết hợp giữa stack và queue. Cách khai báo hoàn toàn tương tự:

#include <deque>

using namespace std;

// Khai báo một queue
deque < {Kiểu_phần_tử} > {Tên_hàng_đợi_hai_đầu};

Các hàm dựng sẵn thông dụng của containers deque được cho trong bảng dưới đây:

2. Trong Python

Đối với Python, ta có khá nhiều cách để biểu diễn hai cấu trúc dữ liệu này. Ngăn xếp và hàng đợi được xây dựng sẵn trong $3$ class là list, collections.deque và queue. Tuy nhiên, cách xây dựng bằng list không tối ưu về mặt thời gian thực thi, nên tôi sẽ không đề cập ở đây.

Nếu như các bạn xây dựng ngăn xếp và hàng đợi bằng class collections.deque, thì nó sẽ tương tự như container deque trong C++, là sự kết hợp giữa stack lẫn queue. Trước tiên, cần import class này, rồi khai báo một biến deque, sử dụng làm stack hay queue tùy theo mục đích. Đây cũng là cách được ưu tiên sử dụng thường xuyên nhất trong Python.

from collections import deque

# Khai báo một ngăn xếp hoặc hàng đợi.
{Tên_biến} = deque()

Những phương thức được dựng sẵn thông dụng sẽ mô tả ở bảng dưới đây. Các bạn sử dụng chúng bằng cú pháp: {Tên_biến}.{Tên_phương_thức}

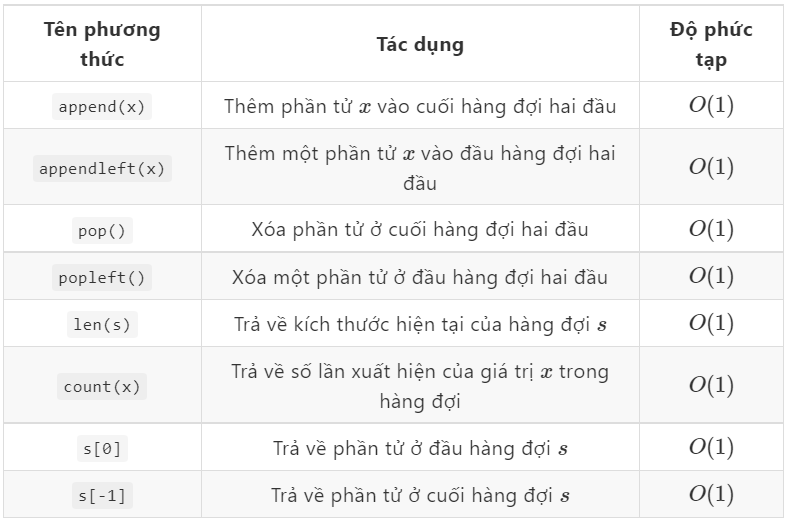
Ngoài ra còn khá nhiều phương thức khác của deque được dựng sẵn, các bạn có thể tham khảo thêm tại đây.

Còn nếu các bạn muốn sử dụng class queue.Queue() và queue.LifoQueue, thì hãy đọc thêm về chúng ở đây. Tuy nhiên, trong class này thời gian thực thi lâu hơn, và lại ít tính năng hơn, nên nó rất ít khi được sử dụng.

VI. Một số bài toán minh họa

1. Kiểm tra ngoặc đúng

Đề bài

Cho một xâu $s$ gồm toàn các dấu ngoặc đóng và mở thuộc ba loại: (), [] và {}. Xâu $s$ được gọi là xâu ngoặc đúng nếu như:

Số lượng ngoặc đóng bằng số lượng ngoặc mở mỗi loại.
Tại mọi vị trí của xâu $s,$ số lượng đóng mỗi loại không vượt quá số lượng ngoặc mở của loại tương ứng.

Hãy kiểm tra xâu $s$ có phải là một xâu ngoặc đúng hay không?

Input:

Một dòng duy nhất chứa xâu $s$ .

Ràng buộc:

$|s| \le 10^6;$ với $|s|$ là độ dài xâu $s$ .

Output:

In ra YES nếu $s$ là xâu ngoặc đúng, ngược lại in ra NO.

Sample Input 1:

{[()]}

Sample Output 1:

YES

Sample Input 2:

{[(])}

Sample Output 2:

NO

Ý tưởng

Sử dụng $1$ stack lưu trữ các dấu ngoặc. Xét kí tự thứ $i$ của chuỗi nhập vào:

Nếu $s_i$ là dấu ngoặc mở thì push vào stack.
Nếu $s_i$ là dấu ngoặc đóng, ta kiểm tra xem dấu ngoặc ở đỉnh của stack có phải ngoặc mở cùng loại không, nếu đúng thì loại bỏ dấu ngoặc đóng khỏi stack, ngược lại đây là xâu ngoặc không cân bằng do đã vi phạm một vị trí $\to$ in NO luôn.

Sau khi duyệt hết xâu, nếu như stack trở thành rỗng thì nghĩa là số lượng ngoặc đóng bằng số lượng ngoặc mở mỗi loại, lúc này ta in ra YES, ngược lại in ra NO.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>

using namespace std;

void enter(string &s)
{
    cin >> s;	
}

void solution(string &s)
{
    stack < char > st;

    for (int i = 0; i < s.size(); ++i)
        switch (s[i])
        {
            case '(': case '[' : case '{':
                st.push(s[i]);
                break;

            case ')':
                if (st.empty() || st.top() != '(')
                {
                    cout << "NO";
                    return;
                }

                st.pop();
                break;

            case ']':
                if (st.empty() || st.top() != '[')
                {
                    cout << "NO";
                    return;
                }

                st.pop();
                break;

            case '}':
                if (st.empty() || st.top() != '{')
                {
                    cout << "NO";
                    return;
                }

                st.pop();
                break;
        }

    if (st.empty())
        cout << "YES";
    else
        cout << "NO";
}

main()
{
    string s;

    enter(s);
    solution(s);
}

Ngôn ngữ Python:

from collections import deque

def solution(s):
    stack = deque()

    for i in range(len(s)):
        if s[i] == '(' or s[i] == '[' or s[i] == '{':
            stack.append(s[i])
        elif s[i] == ')':			
            if len(stack) == 0 or stack[-1] != '(':
                return 0

            stack.pop()
        elif s[i] == ']':
            if len(stack) == 0 or stack[-1] != '[':
                return 0

            stack.pop()
        else:
            if len(stack) == 0 or stack[-1] != '{':
                return 0

            stack.pop()

    return len(stack) == 0

if __name__ == '__main__':
    s = input()

    if solution(s):
        print("YES")
    else:
        print("NO")

2. Đếm số nhị phân

Đề bài

Xét tập các số tự nhiên ở hệ cơ số $10,$ định nghĩa số nhị phân là các số chỉ bao gồm chữ số $0$ và $1$ và không chứa chữ số $0$ vô nghĩa ở đầu. Ví dụ: $1,10, 1001,…$ là các số nhị phân, ngược lại: $123,31,189,…$ không phải các số nhị phân.

Cho trước số nguyên dương $n,$ đếm số lượng số nhị phân không vượt quá $n$ ?

Input:

Một dòng duy nhất chứa số nguyên dương $n$ .

Ràng buộc:

$1 \le n \le 10^9$ .

Output:

In ra số lượng số nhị phân không vượt quá $n$ .

Sample Input:

Sample Output:

Ý tưởng

Ta sẽ sinh ra các số nhị phân lớn hơn dựa vào các số nhị phân nhỏ hơn.

Sử dụng một hàng đợi để lưu danh sách các số nhị phân sinh ra. Ban đầu trong hàng đợi chỉ có số $1$ . Với mỗi số nhị phân $t$ lấy ra từ đầu hàng đợi, hai số $10t$ và $10t + 1$ cũng sẽ là các số nhị phân. Đưa hai số này vào cuối queue nếu như chúng vẫn không vượt quá $n,$ đồng thời đếm số lượng số nhị phân như vậy.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>

using namespace std;

void enter(int &n)
{
    cin >> n;
}

void solution(int n)
{
    queue < int > binary_numbers;
    binary_numbers.push(1);

    int res = 0;
    while (!binary_numbers.empty())
    {
        int cur = binary_numbers.front();
        binary_numbers.pop();

        if (cur <= n)
        {
            ++res;

            binary_numbers.push(cur * 10);
            binary_numbers.push(cur * 10 + 1);
        }
    }

    cout << res << endl;
}

main()
{
    int n;

    enter(n);
    solution(n);
}

Ngôn ngữ Python:

from collections import deque

def enter(n):
    n = int(input())

def solution(n):
    queue = deque()
    queue.append(1)

    res = 0
    while len(queue) > 0:
        cur = queue[0]
        cur.popleft()

        if cur <= n:
            ++res

            queue.append(cur * 10)
            queue.append(cur * 10 + 1)

    print(res)

if __name__ == '__main__':
    n = 0

    enter(n)
    solution(n)

I. Lời mở đầu

II. Ngăn xếp (Stack)

1. Khái niệm

2. Biểu diễn ngăn xếp bằng mảng

III. Hàng đợi (Queue)

1. Khái niệm

2. Biểu diễn hàng đợi bằng mảng

IV. Sử dụng `stack` và `queue` dựng sẵn trong C++ và Python

1. Trong thư viện STL C++

2. Trong Python

VI. Một số bài toán minh họa

1. Kiểm tra ngoặc đúng

Đề bài

Ý tưởng

Cài đặt

2. Đếm số nhị phân

Đề bài

Ý tưởng

Cài đặt

VI. Tài liệu tham khảo

Các Thuật Toán Thường Dùng Cho Bộ Giới Hạn Truy Cập

Thuật toán Manacher - Tìm tất cả xâu con palindrome với độ phức tạp O(N)

Giới thiệu về lý thuyết trò chơi (phần 2)

Geometric Computing Challenges in Competitive Programming

Unordered_map và unordered_set

Set và Map trong C++

Mã hóa RSA hoạt động thế nào?

Một số ứng dụng nâng cao của cây DFS (phần 1)

Thuật toán Floyd-Warshall

Công thức Toán học và Tính chất số học đặc biệt (phần 1)

I. Lời mở đầu

II. Ngăn xếp (Stack)

1. Khái niệm

2. Biểu diễn ngăn xếp bằng mảng

III. Hàng đợi (Queue)

1. Khái niệm

2. Biểu diễn hàng đợi bằng mảng

IV. Sử dụng stack và queue dựng sẵn trong C++ và Python

1. Trong thư viện STL C++

2. Trong Python

VI. Một số bài toán minh họa

1. Kiểm tra ngoặc đúng

Đề bài

Ý tưởng

Cài đặt

2. Đếm số nhị phân

Đề bài

Ý tưởng

Cài đặt

VI. Tài liệu tham khảo

Các Thuật Toán Thường Dùng Cho Bộ Giới Hạn Truy Cập

Thuật toán Manacher - Tìm tất cả xâu con palindrome với độ phức tạp O(N)

Giới thiệu về lý thuyết trò chơi (phần 2)

Geometric Computing Challenges in Competitive Programming

Unordered_map và unordered_set

Set và Map trong C++

Mã hóa RSA hoạt động thế nào?

Một số ứng dụng nâng cao của cây DFS (phần 1)

Thuật toán Floyd-Warshall

Công thức Toán học và Tính chất số học đặc biệt (phần 1)

IV. Sử dụng `stack` và `queue` dựng sẵn trong C++ và Python