Hello mọi người. Trước hết, mình xin cảm ơn mọi người vì đã theo dõi những bài viết của mình trong suốt hai năm vừa qua. Nhân dịp đầu xuân năm mới, mình chúc mọi người một năm mới tiền, tài, sức khỏe phát triển mạnh mẽ như em Dần. 😸

    Chả là thế này từ ngày bắt đầu hành trình học tập và làm việc với bộ môn ML (viết tắt của Machine Learning mọi người nhé ) đến nay cũng khoảng 2 năm rưỡi có lẻ, mình hầu hết học kiến thức về mảng thị giác máy tính. Mình nghĩ đến lúc bản thân cần một cái gì đó mới mẻ nên nhân dịp đầu xuân năm mới, mình thử tập tành về lĩnh vực Xử lý tiếng nói cụ thể hơn trong bài viết này là Text2Speech. Lĩnh vực mới, kiến thức mới nên có thể có những sai xót nhưng với mục đích chia sẻ, trao đổi kiến thức, hy vọng các bạn đọc góp ý để mình có các bài viết về chủ đề này hoàn thiện hơn.

I. Text to Speech và ứng dụng.

    Text to speech là công nghệ chuyển đổi văn bản thành giọng nói. Công nghệ này đã được sử dụng trong nhiều ứng dụng trong đời hằng ngày:

• Sách nói cho người khiếm thị
• Đọc ngoại ngữ như google translate, ...
• Tổng đài tự động

    Text2Speech có lẽ đã không còn mới và đã có nhiều nghiên cứu, giải pháp được đề cập. Và chắc chắn không thể không nhắc đến hai kiến trúc Tacotron và Tacotron2. Hai kiến trúc này là một trong những kiến trúc nền tảng phát triển công nghệ Text2Speech sau này. Trong series này, mình sẽ cùng đi xem qua tổng quan hai em này nhé.

II. Một số kiến thức cơ bản

    Trước khi đi vào nội dung của bài nghiên cứu các kiến trúc cụ thể, mình cùng các bạn tìm hiểu một số kiến thức cơ bản liên quan nhé.

1. Human Speech

1.1. Cách tạo ra âm thanh của con người.

    Giọng nói được tạo ra bởi các sóng âm thanh được tạo ra bởi một loại các bộ phận trong cơ thể thể con người được miêu tả như hình dưới đây:

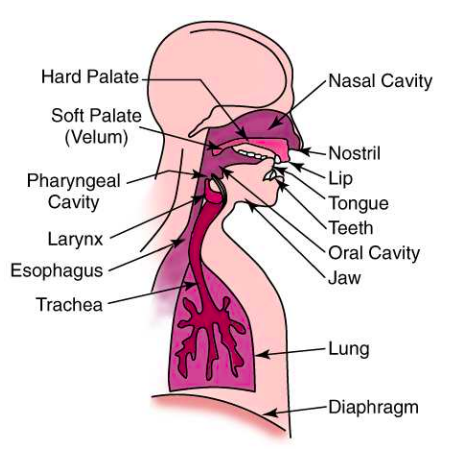
    Âm thanh được tạo ra bởi con người được chia ra làm hai âm:

• Âm hữu thanh
• Âm vô thanh

    Đặc điểm chung cách tạo hai âm thanh này là đều do không khí được đẩy từ phổi (lung) đi qua khí quản (trachea) lên thanh hầu (larynx). Bên trong thanh hầu có các dây thanh (vocal fold/cords). Tuỳ vào vị trạng thái dây thanh khép hay mở sẽ tạo ra âm hữu thanh hoặc âm vô thanh:

    Âm hữu thanh: Khi các dây thanh khép lại, không khí được đẩy từ phổi sẽ tách các dây thanh quản dãn ra liên tục tạo ra hiệu ứng rung động tạo nên âm hữu thanh.

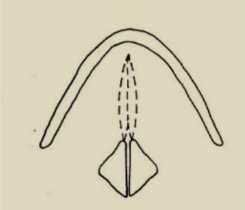
    Âm vô thanh: Khi các dây thanh quản mở ra, không khí từ phổi đẩy đi qua dây thanh quản không bị cản tạo nên âm vô thanh.

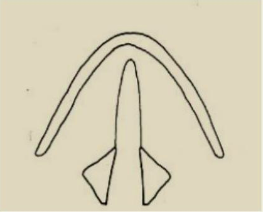
1.2. Âm vị (Phonemes)

    Đơn vị cơ bản nhất của âm thanh. Nếu thay đổi âm vị, nghĩa của từ cũng sẽ thay đổi.

    Ví dụ:

• "pat" -> "bat"
• "pat" -> "pam"

1.3. Formant

    Formant là các tần số cộng hưởng của tuyến phát âm liên quan trực tiếp đến hình dạng, kích thước của cơ quan phát âm nên cung cấp nhiều thông tin đến người nói.

1.4. Đặc tính của âm thanh

    Âm thanh có 4 đặc tính:

• Cao độ (pitch)
• Trường độ (duration)
• Cường độ (amplitude)
• Âm sắc (timbre, tone color)

    Cao độ: đặc trưng độ trầm hoặc bổng của âm thanh. Nốt nhạc thấp cao là kí hiệu biễu diễn cao độ của âm thanh

    Trường độ: Một âm thanh có thể ngân dài hoặc ngắn. Người ta dùng hình nốt khác nhau để định trường độ của âm.

    Cường độ: đặc trưng cho tính mạnh hoặc yếu của âm thanh.

    Âm sắc Mỗi giọng hát, mỗi loại đàn có âm sắc riêng biệt (sáng - tối, trong - đục). Đặc trưng cho tính chất đó người ta gọi là âm sắc.

2. Tín hiệu

    Tín hiệu là một đại lượng vật lý biếu diễn thông tin.

    Ví dụ: Tín hiệu audio là do âm thanh phát ra gây thay đổi áp suất không khí khi đến tai chúng ta. Khi chúng ta thực hiện lấy mẫu với tần số 44.1kHZ tức khoảng 44100 lần / s, ta sẽ thu được sóng (waveform) biễu diễn sự thay đổi của tín hiệu. Chúng ta có thể sửa đổi, phân tích thông tin tín hiệu qua sóng nay bằng máy tính.

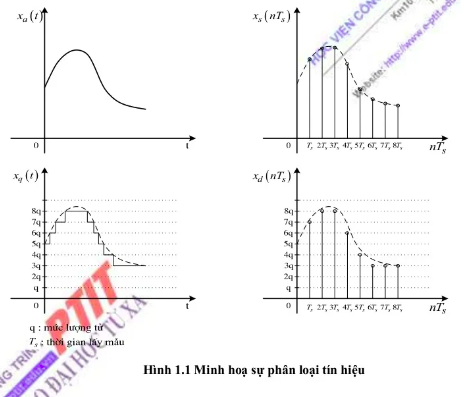
    Tín hiệu sẽ được phân loại như sau:

    Tín hiệu liên tục có biến độc lập của biễu diễn toán học của một tín hiệu là liên tục

• Tín hiệu tương tự có biên độ của tín hiệu liên tục là liên tục.
• Tín hiệu lượng tử hóa có biên độ của tín hiệu liên tục là rời rạc.

    Tín hiệu rời rạc có biến độc lập của biễu diễn toán học của một tín hiệu là rời rạc

• Tín hiệu lấy mẫu có biên độ của tín hiệu rời rạc là liên tục và không bị lượng tử hóa.
• Tín hiệu số có biên độ của tín hiệu rời rạc là rời rạc.

3. Fourier Transform

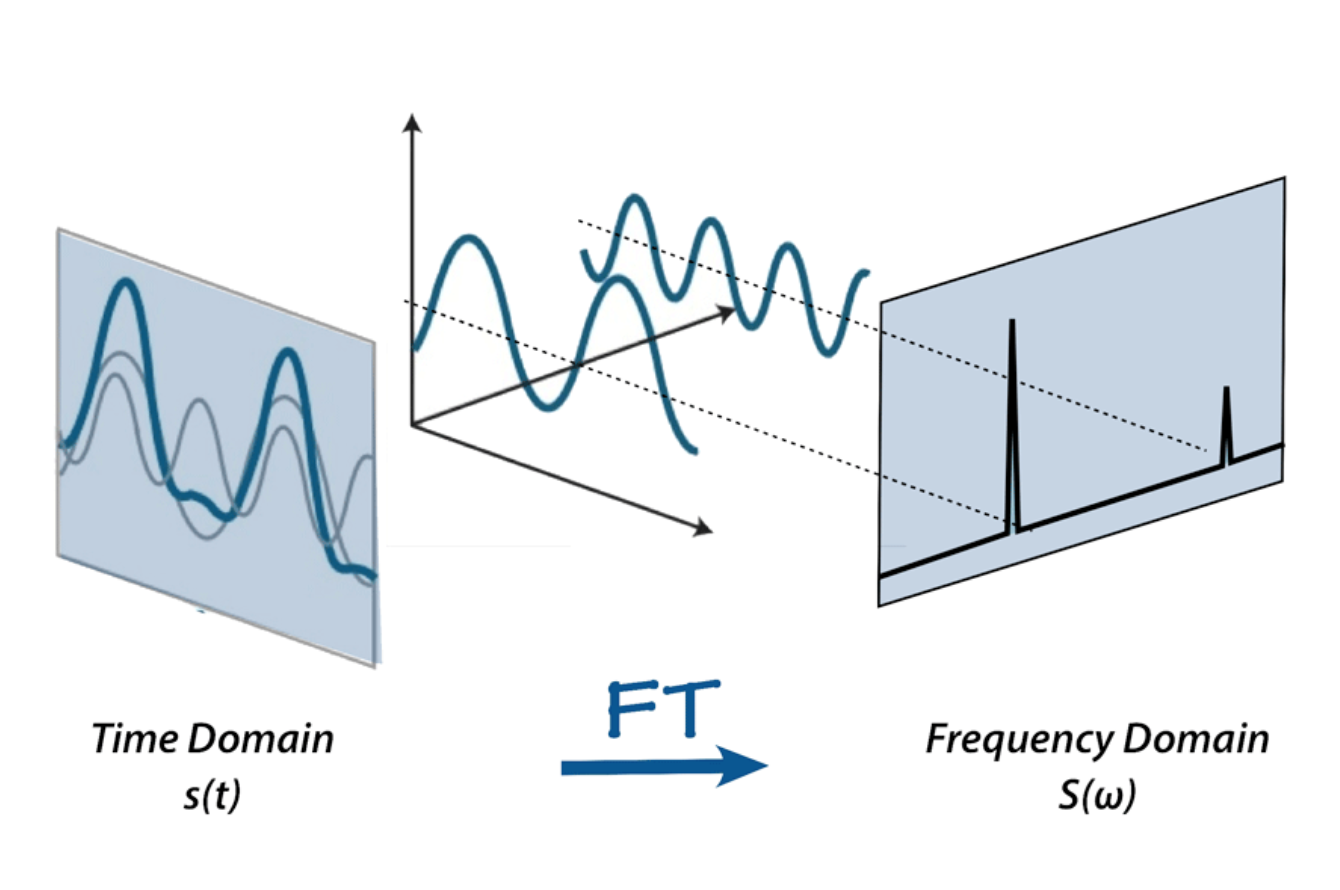
    Fourier Transform là một công cụ giúp chuyển đổi tín hiệu từ miền thời gian về một dạng biểu diễn được gọi là spectrum ở miền tần số. Miền thời gian hay miền tần số đều là các cách biểu diễn của tín hiệu. Và Fourier Transform là cầu nối trung gian giữa hai biểu diễn này. Một sự thay đổi của tín hiệu ở miền kia cũng sẽ ảnh hưởng tín hiệu ở miền khác.

    Ví dụ chúng ta có một sóng có chu kì T được biếu diễn như dưới đây:

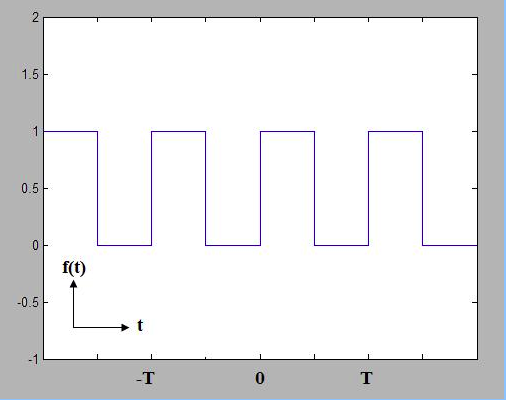     Nguồn: https://www.thefouriertransform.com/series/fourier.php

    Công thức Fourier biếu diễn chuỗi này như sau:

    $$g(t) - = \sum _ { m = 0 } ^ { \infty } a _ { m } \cos ( \frac { 2 \pi m t } { T } ) + \sum _ { n = 1 } ^ { \infty } b _ { n } \sin ( \frac { 2 \pi n t } { T } )$$

    trong đó: $a_m, b_n$ là hệ số của chuỗi Fourier.

4. Discrete Time Fourier Transform

4.1. Khái niệm

    Discrete Time Fourier Transform (DTFT) là phương thức biến đổi giống như Fourier Transform nhưng để giải quyết trong xử lý tín hiệu số.

    Ở đây chúng ta sẽ thắc mắc rằng Tại sao chúng ta là sử dụng tín hiệu số thay vì tín hiệu liên tục ?

    Vì máy tính chúng ta không thể làm việc với tín hiệu liên tục do đó chúng ta cần phải lấy một số lượng mẫu nhất định thay vì dùng tín hiệu gốc. Số lượng mẫu này phải biếu diễn được đặc trưng của tín hiệu

    Ví dụ ta có một tín hiệu liên tục được biểu diễn ở đồ thị dưới đây. Chúng ta thực hiện số lần lấy mẫu L = 8 và tốc đốc lấy mẫu r = 8000 mẫu / giây.

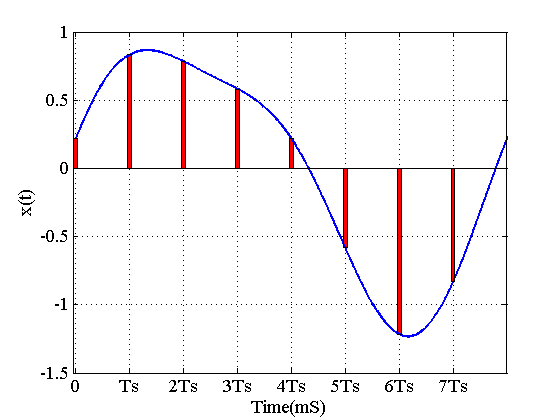     Nguồn: https://www.allaboutcircuits.com/technical-articles/an-introduction-to-the-discrete-fourier-transform/

    Sau đó chúng ta thực hiện chuẩn hóa $T_s = \frac{1}{f_{s}}$, chúng ta sẽ thu được một chuỗi giá trị rời rạc x(n) biếu diễn cho tín hiệu liên tục x(t):

    Các giá trị bên trên là rời rạc. Đó chính là lý do chúng ta cần sử DTFT. Công thức DTFT gồm có hai chiều:

    Chiều thuận:

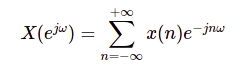
    Chiều ngược:

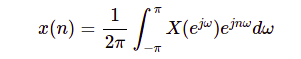
4.2. Giải thích toán học.

    Giống như Fourier Transform, chúng ta mong muốn biến đổi chuỗi tín hiệu rời rạc x(n) đại diện cho các tín hiêu liên tục x(t) thành một tập hợp các sóng sin, cos. Hay nói cách khác từ chuỗi tín hiệu rời rạc đầu vào, ta sẽ tìm các hàm sóng biểu diễn cho các giá trị ấy.

    Gọi $X(e^{jw})$ là hàm tuần hoàn với tần số $2\pi$. Nếu ta lấy N mẫu ở mỗi chu kỳ, khoảng cách giữa hai điểm tần số lấy mẫu là $\frac{2\pi}{N}$. Như vậy tần số của các hàm sin, cos chúng ta mong đợi sẽ có dạng biếu diễn là $\frac{2\pi}{N} \times k$ trong đó $k = 0, 1, ..., N - 1$. Ta có biếu diễn tín hiệu x(n) dưới dạng số phức như dưới đây. Nếu các bạn chưa rõ về biếu diễn chuỗi Fourier với số phức, các bạn có thể tìm hiểu tại bài Fourier Series - Complex Coefficients.

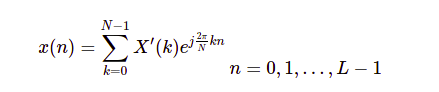
    Với các giá trị L, N và chuỗi giá trị x(n) đã được biết trước, chúng ta có thể giải N giá trị X' bằng hệ phương trình sau:

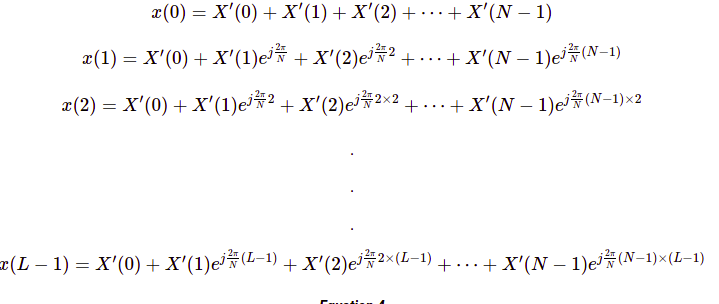
    Sử dụng ngay chuỗi giá trị x(n) rời rạc được trình bày ở phần 3.1 Khái niệm, ta sẽ tính được các giá trị X'(k) như sau:

    Thay các giá trị X'(k) vào, cuối cùng ta tìm được biểu diễn tín hiệu x(n) như sau:

    $$x ( n ) = s i n ( \frac { 2 \pi } { 8 } n ) + 0 . 1 2 5 s i n ( \frac { 4 \pi } { 8 } n ) + 0 . 2 1 6 6 c o s ( \frac { 4 \pi } { 8 } n ) = s i n ( \frac { 4 \pi } { 8 } n ) = s i n ( \frac { 4 \pi } { 8 } n + 3\frac{\pi}{3})$$

    Như vậy thông qua biến đổi DTFT, tín hiệu rời rạc ban đầu có thể biễu diễn ở dạng spectrum ở miền tần số. Phần này mình đọc tài liệu và tham khảo tại bài viết An Introduction to the Discrete Fourier Transform . Các bạn muốn xem chi tiết hơn thì tham khảo bài trên nhé.

5. Fast Fourier Transform

    Fast Fourier Transform (FFT) chức năng giống như DTFT. Tuy nhiên, hiệu quả và nhanh hơn nhiều do giảm được chi phí cho các phép tính toán.

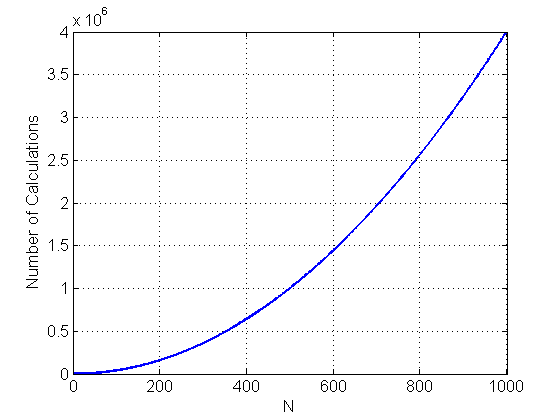
    Theo như bài viết An Introduction to the Fast Fourier Transform, để thực hiện một phép tính với N giá trị lấy mẫu ta cần $4N^{2}$ phép nhân và $N(4N - 2)$ phép cộng. Có thể thấy chi phí tính toán này tỉ lệ thuận với $N^2$ nên khi giá trị N tăng thì chi phí tính toán sẽ bị tăng lên rất nhiều.

     Nguồn: https://www.allaboutcircuits.com/technical-articles/an-introduction-to-the-fast-fourier-transform/

    Đó chính là lý do FFT được ra đời. FFT phân tách N-point DFT thành các DFT có số điểm ít hơn. Ví dụ thực hiện phân tách 1024-point DFT thành 2 512-point DFT, qua đó giảm số phép nhân từ 4,194,304 xuống 2,097,152. Tìm hiểu thêm về FFT, các bạn có thể tham khảo bài viết An Introduction to the Fast Fourier Transform này nhé.

6. Spectrogram.

    Hầu hết các tín hiệu hay gặp đều không tuần hoàn ví dụ như tín hiệu âm thanh hoặc tiếng nói trong khi Fourier Transform chỉ xử lý cho tín hiệu tuần hoàn. Và từ đây ý tưởng dùng FFT cho từng đoạn nhỏ hơn được ra đời.

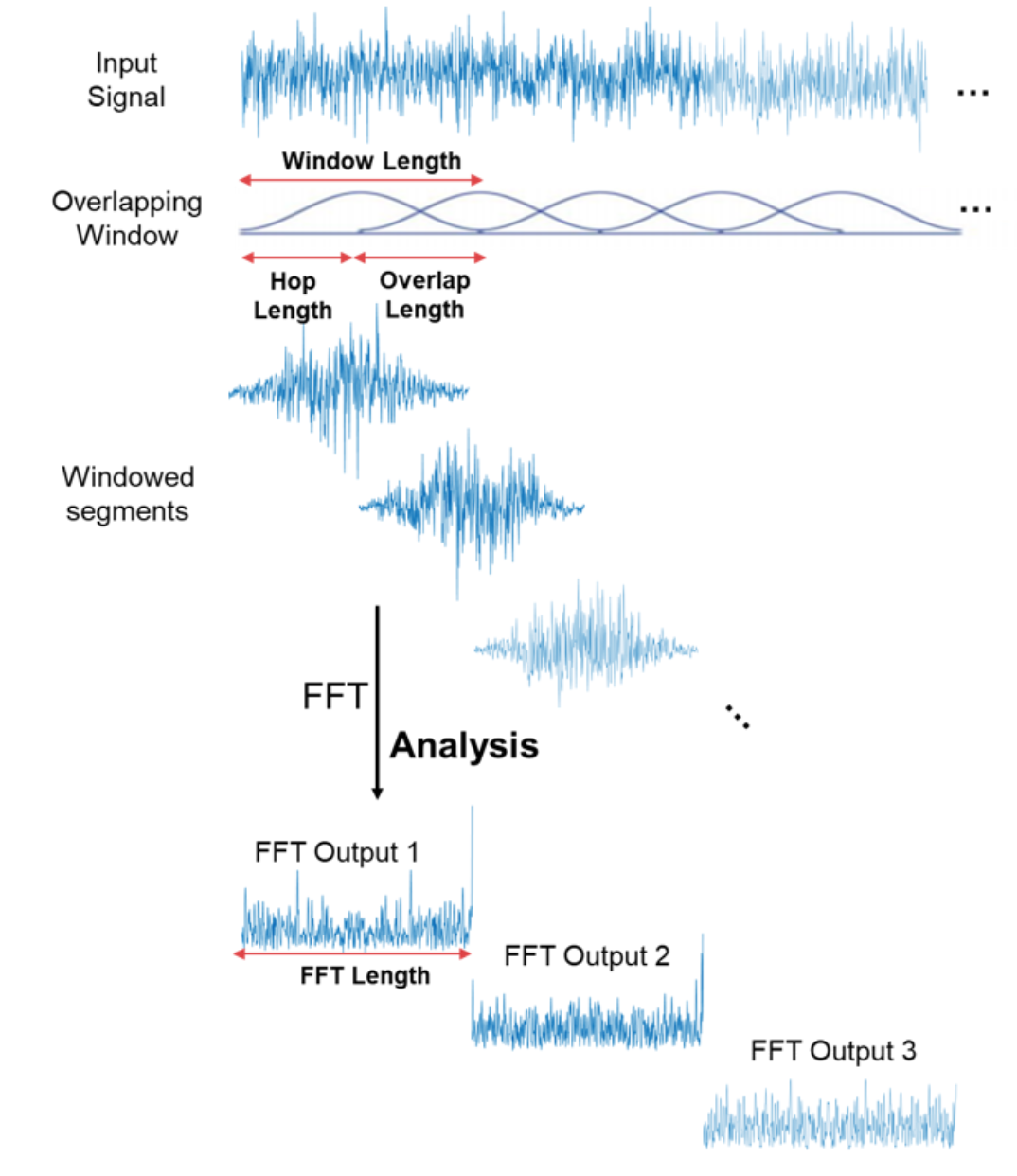
    Ở đây mình có một số khái niệm như sau:

• Window length: Chiều dài cố định các khoảng mà FFT chia tín hiệu.
• Hop length: Chiều dài phần không giao nhau giữa hai window.
• Overlap length: Chiều dài của phần giao nhau giữa hai window.

    Để biểu diễn kết quả tính của FFT, ta dùng một khái niệm gọi là Spectrogram. Spectrogram là biễu diễn kết quả của nhiều FFT trên phần window length.

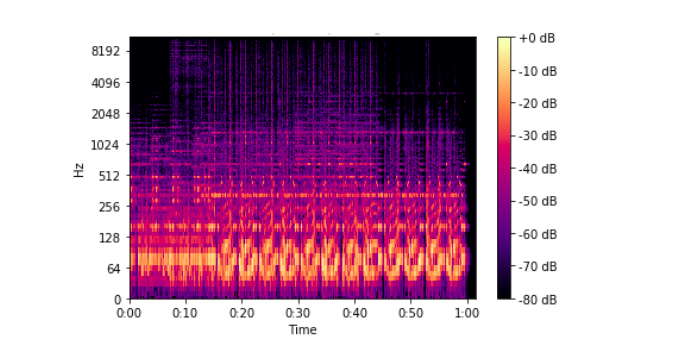
    Mỗi đơn vị trên trục y tương ứng với tần số ở log scale và mỗi đơn vị ở giá trị x tương ứng với window length được dùng để tính FFT. Mỗi giá trị (x, y) biểu diễn cường độ tín hiệu ở dB scale tương ứng với window length và tần số.

7. Mel Scale

    Các nghiên cứu đã chỉ ra rằng tai người dễ dàng phân biệt các âm thanh ở tần số 500-1000 Hz. Tuy nhiên khó phân biệt các âm thanh ở tần số 7500-8000 Hz hoặc nói cách khác là tai người nghe các âm ở vùng tần số này giống nhau.

    Để biếu diễn thang đo phù hợp tai người, chúng ta dùng một thang đo được gọi Mel Scale.

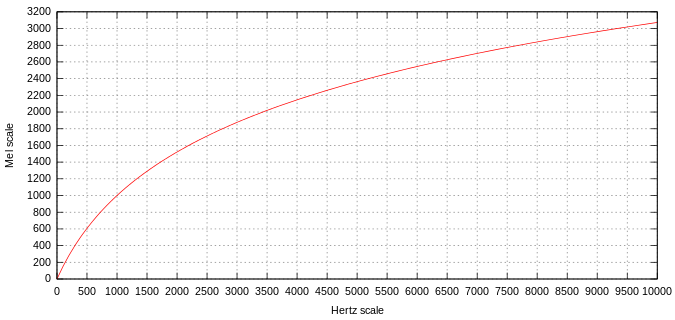
    Công thức chuyển đổi từ Hz scale sang Mel scale như sau:

    $$m = 2 5 9 5 \log _ { 1 0 } \left( 1 + { \frac { f } { 7 0 0 } } \right)$$

8. Mel Spectrogram

    Mel Spectrogram về cơ bản giống như Spectrogram tuy nhiên trục tần số tức là trục x không ở Hz scale mà ở Mel scale để phù hợp với khả năng nghe của con người.

III. Lời kết.

    Trong bài này, mình đã giới thiệu qua một số kiến thức nền tảng về chủ đề Xử lý giọng nói. Việc nắm chắc các kiến thức cơ bản giúp các bạn hiểu rõ hơn cách tạo ra giọng nói, kiến trúc của những thuật toán sau này. Ở các bài sau, mình sẽ đi sâu vào phần các thuật toán Text2Speech. Nếu các bạn thấy bài viết hay thì hãy cho mình một upvote nhé. 😁 Gặp lại các bạn trong các bài về chủ đề này tiếp theo.

Tài liệu tham khảo

1.     Nghiên cứu kỹ thuật nhận dạng người nói dựa trên từ khoá tiếng Việt, 2010

2.     Ngữ âm học

3.     Human Speech Processing Phonetics and Phonology

4.     ECE438 - Laboratory 9: Speech Processing

5.     Understanding the Mel Spectrogram

6.     Fourier Series

7.     Terms you need to know to start Speech Processing with Deep Learning

8.     Xử lý tín hiệu số

9.     An Introduction to the Discrete Fourier Transform

10.     An Introduction to the Fast Fourier Transform