I. Dãy Fibonaci

Dãy số Fibonaci được xác định bởi công thức sau:

$\begin{cases}f_0 = 0.\\f_1 = 1.\\ f_i = f_{i - 1} + f_{i - 2},&\text{với }i \ge 2.\end{cases}$

Một số phần tử đầu tiên của dãy Fibonaci là: $0, 1, 1, 2, 3, 5, 8$ Ngoài ra, số Fibonaci thứ $N$ còn có thể tính bằng công thức tổng quát:

$f_N = \frac{1}{\sqrt{5}}\times \left[\left(\frac{1 + \sqrt{5}}{2}\right)^N - \left(\frac{1 - \sqrt{5}}{2}\right)^N\right] \ (1)$

Dãy Fibonaci là đáp án của một số bài toán dưới đây:

1. Bài toán cổ về các cặp thỏ

Phát biểu bài toán:

Ban đầu chỉ có một cặp thỏ được sinh ra.
Hai tháng sau khi ra đời, mỗi cặp thỏ sẽ sinh ra một cặp thỏ con mới.
Khi đã sinh con rồi thì cứ mỗi tháng tiếp theo, chúng lại sinh được một cặp con mới.
Giả sử các con thỏ không bao giờ chết, hãy đếm số lượng cặp thỏ ở tháng thứ $N?$

Ví dụ: Với $N = 5,$ ta thấy:

Giải thích:

Giữa tháng thứ nhất: $1$ cặp (cặp ban đầu).
Giữa tháng thứ hai: $1$ cặp (cặp ban đầu vẫn chưa đẻ).
Giữa tháng thứ ba: $2$ cặp (cặp ban đầu đẻ thêm một cặp con).
Giữa tháng thứ tư: $3$ cặp (cặp ban đầu tiếp tục đẻ).
Giữa tháng thứ năm: $5$ cặp (cặp ban đầu tiếp tục đẻ và cặp thứ hai bắt đầu đẻ).

2. Bài toán xếp Domino

Phát biểu bài toán: Đếm số cách xếp $N - 1$ thanh Domino có kích thước $2 \times 1$ để phủ kín một bảng ô vuông kích thước $2 \times (N - 1)$ .

Ví dụ: Có $8$ cách khác nhau để xếp các thanh Domino kích thước $2 \times 1$ phủ kín bảng $2 \times 5 \ (N = 6, f_6 = 8)$ :

3. Cài đặt

Đối với các giá trị $N \ (N \le 10^7)$ không quá lớn, ta có thể tính trực tiếp số Fibonaci bằng công thức truy hồi $f_i = f_{i - 1} + f_{i - 2}$ . Trong trường hợp $N$ lớn, cần phải sử dụng Phép nhân ma trận để tính toán, bài toán này sẽ được đề cập tới sau.

Cài đặt bằng công thức truy hồi:

long long fibo(int N)
{
    if (N <= 1)
        return N;

    int fi_2 = 0, fi_1 = 1, cur_fi = 0;
    for (int i = 2; i <= N; ++i)
    {
        cur_fi = fi_1 + fi_2;
        fi_2 = fi_1;
        fi_1 = cur_fi;
    }
        
    return fi_ntext;
}

II. Dãy Catalan

Số Catalan được xác định bởi công thức sau:

$Catalan_N = \frac{1}{N + 1}\times C_{2N}^{N} = \frac{(2N)!}{(N + 1)! \times N!}; \text{với } N \ge 0$

Một số phần tử đầu tiên của dãy Catalan là: $1, 1, 2, 5, 14, 42, 132,...$

Số Catalan là đáp án của các bài toán sau:

1. Bài toán đặt ngoặc

Phát biểu bài toán: Cho trước số nguyên không âm $N,$ hãy đếm số cách khác nhau để đặt $N$ dấu ngoặc mở và $N$ dấu ngoặc đóng đúng đắn. Cách đặt ngoặc đúng đắn có thể phát biểu đệ quy như sau:

$()$ là một cách đặt ngoặc đúng.
Nếu $X$ là một cách đặt ngoặc đúng thì $(X), ()X$ và $X()$ cũng là cách đặt ngoặc đúng.

Ví dụ: Với $N=3,$ ta có $5$ cách đặt ngoặc đúng sau:

$((())), (()()), (())(), ()(()), ()()()$

2. Đếm cây nhị phân

Phát biểu bài toán: Cho trước số nguyên không âm N, hãy đếm số cây nhị phân khác nhau có đúng $(N+1)$ lá?

Ví dụ: Với $N = 3$ :

3. Chia đa giác

Phát biểu bài toán: Cho một đa giác lồi gồm $(N+2)$ đỉnh. Ta chia đa giác thành các tam giác bằng cách vẽ các đường chéo không cắt nhau trong đa giác. Hỏi có bao nhiêu cách chia như vậy?

Ví dụ: Với $N = 4$ :

4. Cài đặt

Dưới đây cài đặt chương trình tính số Catalan thứ $N \ (N \le 10^6)$ và đưa ra kết quả là phần dư sau khi chia cho $10^9+7$

long long modular_exponentiation(long long A, long long B, long long M)  // Tính A^B % M.
{
    if (B == 0)
        return 1LL;

    long long half = modular_exponentiation(A, B / 2LL, M) % M;

    if (B & 1)
        return (((half * half) % M) * (A % M)) % M;
    else
        return (half * half) % M;
}

long long inverse_modulo(long long A, long long M) // Nghịch đảo modulo M của A.
{
    return modular_exponentiation(A, M - 2, M);
}

long long catalan_N(long long N, long long M)
{
    long long x = 1, y = 1;
    for (int i = N + 2; i <= 2 * N; ++i)
        x = (x * i) % M;
    for (int i = 1; i <= N; ++i)
        y = (y * i) % M;
    y = inverse_modulo(y, M);

    return (x * y) % M;
}
    
int main()
{
    long long M = 1e9 + 7;
    cout << catalan_N(N, M);
}

III. Số Euler (Eulerian Number)

Số Euler $A(N, M)$ là số lượng hoán vị của các số từ $1$ tới $N$ mà có đúng $M$ số lớn hơn số đứng liền trước nó. Lấy ví dụ, với $N = 3, M = 1,$ có $4$ hoán vị từ $1$ tới $3$ mà có đúng $1$ số lớn hơn số liền trước nó, thể hiện trong bảng dưới đây:

Số Euler là hệ số của đa thức Euler bậc $M$ với công thức:

$A_N(t) = \sum_{M = 0}^N A(N, M)\times t^M$

Ta có thể tính số Euler bằng hệ thức truy hồi sau:

$A(N, M) = \begin{cases}0, &\text{với } M \ge N \text{ hoặc } N = 0.\\ 1, &\text{với } M = 0. \\(N - M)\times A(N - 1, M - 1) + (M + 1) \times A(N - 1, M), &\text{trường hợp khác.}\end{cases}$

Cài đặt: Dưới đây cài đặt chương trình tính số Euler bằng đệ quy, ngoài ra bạn đọc có thể suy nghĩ cách cài đặt bằng quy hoạch động:

long long euler_number(int N, int M)
{
    if (M == 0)
        return 1;
        
    if (M >= N || N == 0)
        return 0;
            
    return (N - M) * euler_number(N - 1, M - 1) + 
           (M + 1) * euler_number(N - 1, M);
}

IV. Tam giác Pascal:

Tam giác Pascal là một công thức xác định các tổ hợp chập $k$ của $n,$ bằng tính chất của tổ hợp: $C^k_n = C^{k - 1}_{n - 1} + C^k_{n - 1} \ (0 < k < n)$ . Quy ước hàng đầu tiên của tam giác là $n = 0$ có duy nhất một số $1$ - để biểu thị cho $C^0_0 = 1,$ . Sử dụng công thức truy hồi, chúng ta dễ dàng tính được tam giác Pascal với vị trí hàng $n,$ cột $k$ là số lượng tổ hợp chập $k$ của $n$ (coi các vị trí trống là 0). Ở mỗi hàng, cột đầu tiên và cột cuối cùng luôn mang giá trị $1,$ thể hiện cho tính chất $C^0_n = C^n_n = 1$ . Hình vẽ dưới đây minh họa cho tam giác Pascal với các hàng từ $0$ tới $7$ :

Ngoài ra, tam giác Pascal còn sử dụng để tính các hệ số của khai triển nhị thức Newton bậc $N \ (a + b)^N$ thành một đa thức có $N+1$ số hạng. Nhị thức này đã được chứng minh bởi Issac Newton vào năm $1665,$ với công thức như sau:

$(a+b)^N=\sum_{k = 0}^N C^k_N\times a^{n - k} \times b^k$

Cài đặt: Xây dựng tam giác Pascal gồm

N

hàng:

void pascal_triangle(int N)
{
    for (int i = 0; i <= N; ++i) // Cột đầu tiên của mọi hàng bằng 1.
        c[i][0] = 1;

    for (int i = 1; i <= N; ++i)
        for (int j = 1; j <= i; ++j)
            c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
}

V. Công thức bao hàm - loại trừ:

Công thức bao hàm - loại trừ là một công thức sử dụng để tính lực lượng (số lượng phần tử) của hợp của nhiều tập hợp. Công thức được phát biểu như sau: "Để tính lực lượng của hợp của nhiều tập hợp, ta tính tổng lực lượng các tập hợp đó, rồi trừ đi lực lượng của giao của các cặp hai tập hợp khác nhau, rồi cộng lực lượng của giao các bộ ba tập hợp khác nhau, rồi trừ đi lực lượng của các bộ bốn tập hợp, và cứ thế cho đến khi ta xét đến giao của tất cả các tập hợp."
Đối với các tập hợp, công thức có thể được viết ở dạng như sau: Giả sử có $N$ tập hợp $A_1, A_2, A_3,..., A_N$ . Lực lượng của hợp của $N$ tập hợp là: $|\bigcup_{i=1}^N A_i| = \sum_{i=1}^n |A_i| - \sum_{i \ne j} |A_i \cap A_j| + |A_1 \cap A_2 \cap A_3| + |A_1 \cap A_2 \cap A_4| + \cdots +$ $|A_{N-2} \cap A_{N-1} \cap A_N| - \cdots - (-1)^n|A_1 \cap A_2 \cap … \cap A_N|$
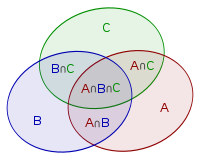
    Ta có thể minh họa công thức bằng một sơ đồ Venn trong trường hợp $N = 3$ như sau:



    Như sơ đồ, ta thấy lực lượng của $A \cap B \cap C$ bằng tổng lực lượng của $A, B, C$ trừ đi lực lượng của các giao $A \cap B, B \cap C, C \cap A$ rồi cộng thêm lực lượng của $A \cap B \cap C$ :

$| A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|$

Bằng phương pháp tương tự ta có thể minh họa được công thức với $N$ tập hợp.

Ví dụ: Đếm số lượng số từ $1$ $1$ tới $N$ $N$ và không chia hết cho số nào trong tập $\{2, 3, 5\}$ ${2, 3, 5}$ :
```
int count_numbers(int N)
{
    return N - N / 2 - N / 3 - N / 5 + N / (2 * 3) +
           N / (3 * 5) + N / (2 * 5) - N / (2 * 3 * 5);     
}
```
Ta có thể biến đổi bài toán thành đếm phần bù: Đếm số lượng phần tử chia hết cho ít nhất một số trong tập $\{2, 3, 5\}$ ${2, 3, 5}$ rồi lấy $N$ $N$ trừ đi số lượng đó. Đặt $A$ $A$ là tập hợp các phần tử chia hết cho $2,\ B$ $2, B$ là tập hợp các phần tử chia hết cho $3, \ C$ $3, C$ là tập hợp các phần tử chia hết cho $5$ $5$ từ 1 tới $N$ $N$ . Cần tính $|A \cup B \cup C|$ $∣ A \cup B \cup C ∣$ . Dựa vào công thức bao hàm, loại trừ, ta có:

$| A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|$

$=\left \lfloor{\frac{N}{2}} \right \rfloor+\left \lfloor{\frac{N}{3}} \right \rfloor+\left \lfloor{\frac{N}{5}} \right \rfloor-\left \lfloor{\frac{N}{2.3}} \right \rfloor-\left \lfloor{\frac{N}{2.5}} \right \rfloor-\left \lfloor{\frac{N}{3.5}} \right \rfloor+\left \lfloor{\frac{N}{2.3.5}} \right \rfloor$

I. Dãy Fibonaci

1. Bài toán cổ về các cặp thỏ

2. Bài toán xếp Domino

3. Cài đặt

II. Dãy Catalan

1. Bài toán đặt ngoặc

2. Đếm cây nhị phân

3. Chia đa giác

4. Cài đặt

III. Số Euler (Eulerian Number)

IV. Tam giác Pascal:

V. Công thức bao hàm - loại trừ:

Tài liệu tham khảo:

Matrix Exponentiation - Simplifying Complex Calculations

Một số dãy số đặc biệt (Fibonacci, Catalan, Euler)

Tìm hiểu về thuật toán Quick sort

[Lập trình C++ cơ bản] Bài 2: Toán tử và Toán hạng

Ngăn xếp và Hàng đợi (Stack và Queue)

Tìm kiếm dữ liệu nhanh với mẹo tìm kiếm nhị phân

Hamilton Graphs and Hamiltonian Cycles

Sorting Functions in STL C++

Tất cả những gì bạn cần là quy hoạch động

[Lập trình C++ cơ bản] Bài 9: Địa chỉ và Con trỏ (phần 1)