Chào các bạn đã trở lại với series về Paper Explain - Series giải thích chi tiết về các paper trong lĩnh vực AI. Paper hôm nay chúng ta sẽ tìm hiểu là một paper rất hay, nó mang tên What’s Hidden in a Randomly Weighted Neural Network?. Paper này không bàn về một kiến trúc mạng mới mà nói về một tư tưởng mới trong việc training mạng nơ ron. Từ xưa đến nay thì chúng ta vẫn nghĩ rằng việc training một mạng nơ ron là đi tối ưu các trọng số của mô hình để đạt được một mức độ chính xác nào đó. Paper này đặt một vấn đề ngược lại, thay vì sử dụng một optimizer và cập nhật các trọng số để đi tìm các giá trị tối ưu cho các node của mạng thì tại sao không thử đi tìm một tập hợp các node được khởi tạo ngẫu nhiên từ một random distribution để khi liên kết các node đó lại chúng ta sẽ thu được độ chính xác mong muốn. Hay nói cách khác, thay vì cố định một architecture và học các trọng số thì tại sao không cố định các trong số và học architecture? Đó là câu hỏi chúng ta sẽ cùng nhau tìm hiểu trong suốt paper này. Hi vọng nó sẽ mở ra cho các bạn nhiều trải nghiệm mới cũng như các hướng đi mới trong việc nghiên cứu các mô hình AI. OK Let Go ..... chúng ta bắt đầu ngay thôi

Sơ lược về paper

    Paper này mạng tên What’s Hidden in a Randomly Weighted Neural Network? được đăng tại hội thảo hàng đầu trong lĩnh vực AI - CVPR 2020 nên chúng ta không cần phải bàn xét nhiều về vấn đề chất lượng của nó nữa nhé. Paper này được viết bởi nhóm nghiên cứu Allen Institute for Artificial Intelligence và các tác giả thuộc đại học Washington. Chúng ta sẽ cùng tìm hiểu về vấn đề mà paper này sẽ giải quyết nhé.

    Trong phần abstraction chúng ta rút ra được vài ý như sau:

• Việc training mạng nơ ron bằng cách học giá trị các trọng số weights của mạng đã rất quen thuộc với chúng ta từ trước
• Tác giả đề xuất việc học một subnetwork với giá trị các weights được khởi tạo ngẫu nhiên mà không làm thay đổi bất kì tham số nào của mạng ban đầu
• Tác giả chứng minh hiệu quả bằng việc học một subnetwork từ mạng Resnet50 được khởi tạo ngẫu nhiên cho kết quả tương đương với mạng Resnet34 được train trên tập Imagenet
• Và điểm quan trọng nhất là tác giả cung cấp một thuật toán để giúp tìm ra subnetwork đó.

    Ngắm nghía biểu đồ bên tay phải một chút để dễ hình dung hơn về bài toán này nhé

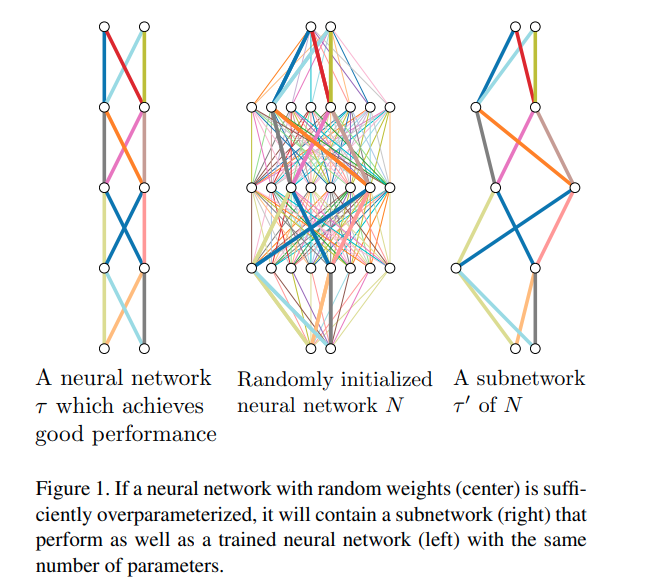
    Bên tay trái giả sử là một mạng nơ ron đã được học rất tốt trên một tập dữ liệu (giả sử Imagenet) kí hiệu là $\tau$. Ở giữa là một mạng nơ ron được khởi tạo ngẫu nhiên các tham số kí hiệu là $N$. Và bên phải là một subnetwork của $N$ kí kiệu là $\tau'$. Sao cho hiệu suất của hai mạng $\tau$ và $\tau'$ là tương đương nhau.

Các vấn đề liên quan

    Trước khi đi sâu vào các vấn đề cụ thể trong paper chúng ta cùng tìm hiểu một số vấn đề liên quan đến paper này nhé

Lottery Tickets and Supermasks

    Đây là một nghiên cứu rất hay, nó được đề cập trong paper THE LOTTERY TICKET HYPOTHESIS: FINDING SPARSE, TRAINABLE NEURAL NETWORKS. Paper này phát hiện ra rằng có tồn tại một subnetwork (sparse network) ẩn chứa trong một neural network nhưng có thể được train một cách hiệu quả khi retrain from scratch khi chúng ta reset to their initialization. Nó còn được gọi là một winning ticket trong trò chơi initialization lottery. Hypothesis này được phát biểu như sau

    A randomly-initialized, dense neural network contains a subnetwork that is initialized such that—when trained in isolation—it can match the test accuracy of the original network after training for at most the same number of iterations.

    Tác giả đề xuất phương pháp tìm ra winning ticket bằng thuật toán sau:

• Sau khi training network lớn, áp dụng kĩ thuật pruning để set tất cả các weight nào có magnitude nhỏ hơn một ngưỡng threshold về 0
• Khởi tạo lại các phần weight còn lại về phân phối ban đầu
• Training lại mạng với các tham số được khởi tạo lại nhưng các weight đã được set về 0 sẽ bị đóng băng (frozen) hay không được train.

    Paper này đặt ra một số câu hỏi cho chúng ta như: Tại sao mask và initialization lại liên kết chặt chẽ với nhau đến vậy. Thậm chí khi ta khởi tạo một phân phối khác trên mask đó có thể dẫn đến mạng không thể học được trong retrain. Tức là chúng ta không thể training một mạng đã được pruned với một initialization khác với distribution lúc đầu.

    Tiếp nối các hoạt động của paper Lotery Ticket, nhóm tác giả của Uber AI Research trong paper Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask_ đã đưa ra khái niệm supermask - một subnetwork của một network lớn được tạo ra bằng cách khởi tạo trên một random distribution mà có thể đạt được độ chính xác tương đương với mạng đã được training dù cho nó không cần phải training với dữ liệu. Đối với tập CIFAR-10 họ có thể tìm được một supermask đạt được độ chính xác 65.4% mà không cần tối ưu trọng số của mạng. Thuật toán của họ đưa ra như sau: với mỗi weight $w$ của mạng lúc đầu đạt một giá trị xác suất $p$. Trong quá trình forward của model, trọng số của $w$ sẽ được sử dụng với xác suất $p$ hoặc được đặt về 0. Hay tương đương với việc họ sử dụng một weight $w' = w*X$ trong đó $X$ là một biến ngẫu nhiên tuân theo phân phối Bernouli (X nhận giá trị 1 với xác suất là $p$ và 0 với xác suất $1-p$).

    Trong quá trình forward của mạng, weight $w$ sẽ được xuất hiện với xác suất $p$ hoặc được reset bằng 0. Để thực hiện việc này thì các tác giả Zhou và cộng sự đã tạo ra một mask được khởi tạo ngẫu nhiên sau đó đưa qua hàm sigmoid để đưa về khoảng $0\leq input_i\leq 1$. Sau đó được đưa tiếp qua một hàm Bernoulli để tạo ra binary mask với xác suất p.

    $$out_i \sim Bernoulli(p=input_i)$$

    Xác suất $p$ này là đầu ra của activation sigmoid và được học sử dụng các giải thuật optimizer như SGD hay Adam. Việc tìm supermask tương đương với việc tìm một binary mask cho trọng số của mô hình.

    Paper của chúng ta được lấy cảm hứng từ paper Deconstructing Lotery Ticket kể trên nhưng cải tiến bằng cách dưa ra một thuật toán hiệu quả hơn để tìm kiếm supermask

Neural Architecture Search - NAS

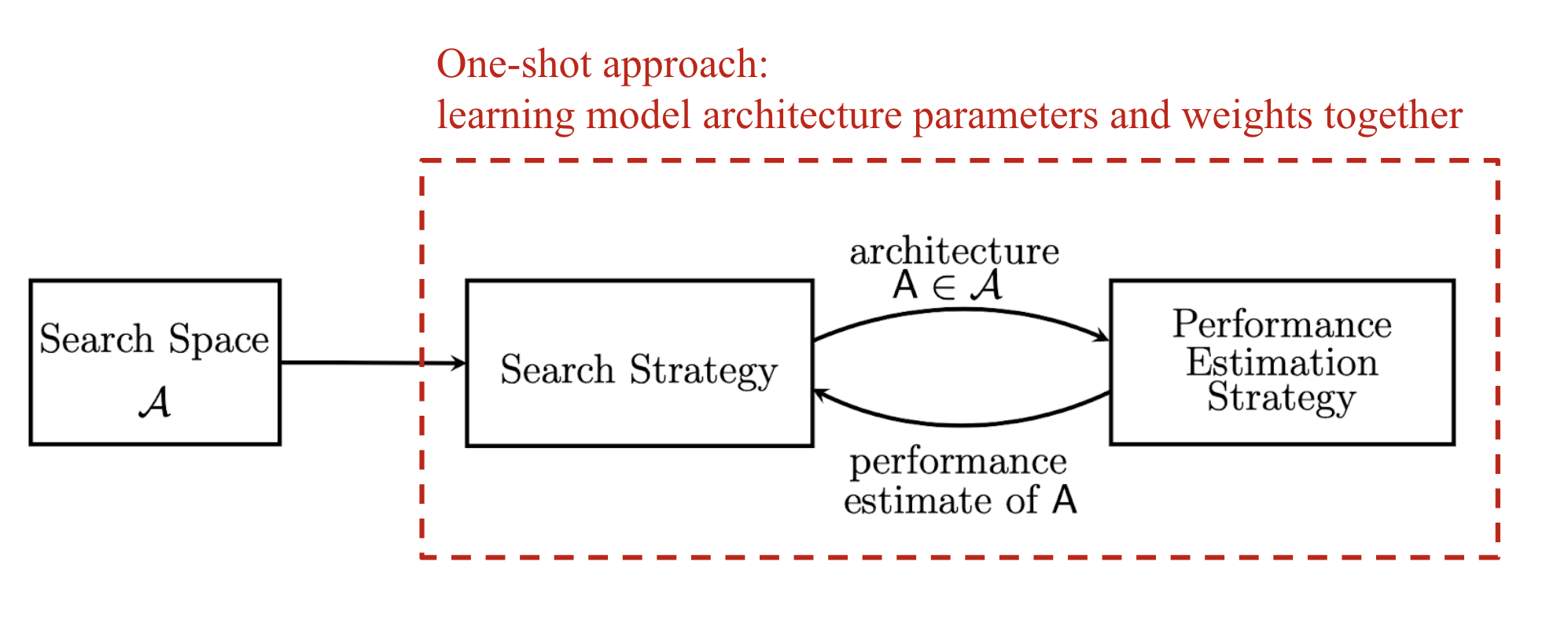
    Sự ra đời của các mô hình neural networks hiện đại đã làm thay đổi cách người ta xử lý dữ liệu từ feature engineer thủ công sử dụng đến nhiều expertise của các chuyên gia sang việc feature learning sử dụng cách mạng neural. Tuy nhiên các researcher vẫn đang lựa chọn kiến trúc của mô hình một cách thủ công. Từ đó ý tưởng về Neural Architecture Search ra đời. Một trong những áp dụng nổi tiếng nhất của nó đó chính là EfficientNet - Rethinking Model Scaling for Convolutional Neural Networks SOTA của Image Recognition task dựa trên supervised learning cho đến hết năm 2020. (Đầu năm 2021 chứng kiến sự ra đời của NF-Net High-Performance Large-Scale Image Recognition Without Normalization đã phá vỡ kỉ lục của các một hình supervised learning trên ImageNet Image Classification Task). Nhìn chung một hệ thống NAS có thể được chia thành 3 thành phần chính (theo survey Neural Architecture Search: A Survey):

• Search Space: Một NAS Search Space định nghĩa một tập hợp các operations như convulution, fully connected, pooling, dropout ... và cách mà các operations này kết nối với nhau để tạo thành một kiến trúc mạng. Việc thiết kế search space thường đòi hỏi expertise của con người và thường bị ảnh hưởng khá nhiều bởi ý kiến chủ quan của người thiết kế.
• Search Algorithm: nhận đầu vào là một tập hợp các ứng cử viên trong search space. Mục tiêu của nó là dựa vào performance của từng model nhỏ trong search space (high accuracy, low latency...) để tối ưu để tạo ra các high performance architecture.
• Evaluation Strategy: Cần phải có một bộ tiêu chí đánh giá tương tự như hàm loss trong quá trình tối ưu mạng nơ ron để có thể feedback cho Search Algorithm biết cách cập nhật lại các architecture. Chúng ta có thể hình dung toàn bộ quá trình trong sơ đồ sau.

Straight-through gradient estimators

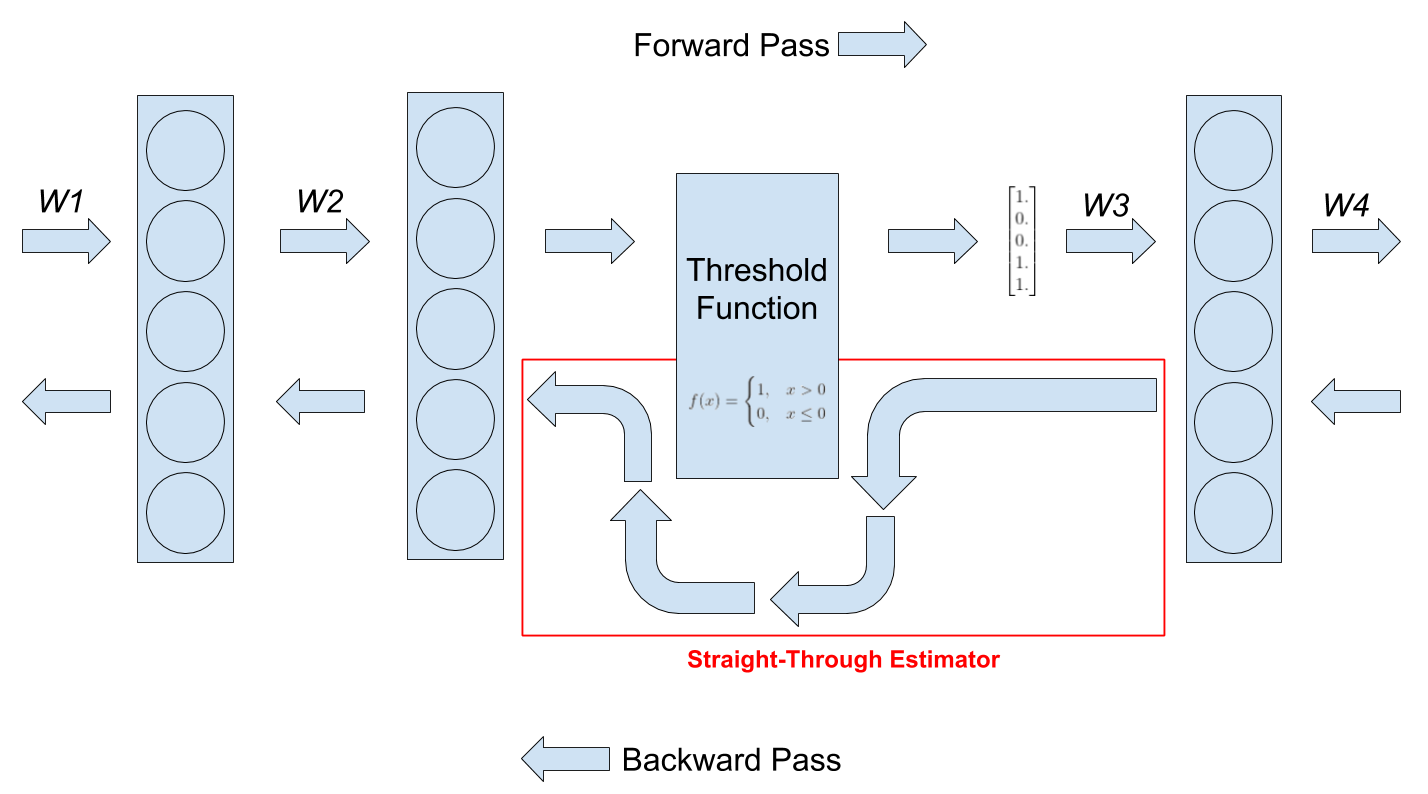
    Straight-through gradient estimators - STE là một kĩ thuật được đề cập trong bài báo này. Nó được đề xuất từu một paper của Bengio và cộng sự vào năm 2013 Estimating or propagating gradients through stochastic neurons for conditional computation. Chúng ta đôi lúc sẽ xuất hiện những tình huống trong thiết kế mạng nơ ron như:

• Thỉnh thoảng, chúng ta muốn đưa một hàm threshold vào trong một mạng nơ ron để biến đổi các giá trị thành output của một layer. Có rất nhiều lý do để chúng ta muốn thực hiện điều này ví dụ như khi chúng ta muốn chuyển các giá trị của activation function sang dạng binary ví dụ như sau:

    $$f(x)= \begin{cases}1, & x>0 \\ 0, & x \leq 0\end{cases}$$

• Tuy nhiên một vấn đề đó là trong quá trình back propagate thì các hàm threshold như trên sẽ có đạo hàm bằng 0 và nó làm cho mạng của chúng ta không học được gì
• Một kĩ thuật để xử lý vấn đề đó chính là straight-through estimators (STE)

    Như đã nói ở trên, một vấn dề xuất hiện trong các hàm threshold đó là đạo hàm của chúng sẽ bằng 0 và để loại bỏ vấn đề này chúng ta sẽ sử dụng STE như một phương pháp trong quá trình backward pass. STE sẽ ước tính giá trị đạo hàm của môt hàm bằng cách bỏ qua đạo hàm của hàm threshold trong quá trình backward và gradient được lan truyền về cách layer trước đó. Lúc này gradient của hàm threshold được coi như gradient của một hàm đồng nhất (identity function) tức có đầu ra bằng với đầu vào $f(x) = x$. Chúng ta có thể hình dung rõ hơn trong hình sau

Hướng tiếp cận của bài báo

Cách để tìm được good subnetwork

    Trong paper tác giả đã đưa ra phương pháp cải tiến để tìm kiếm một subnetwork hiệu quả. Việc tìm kiếm một subnetwork trong một mạng con được khởi tạo từ random weights cũng đã được trình bày trong paper Deconstructing lottery tickets như đã thảo luận ở phần trên. Giải thuật mà tác giả đề xuất được gọi là edge-popup được mô tả trong hình sau

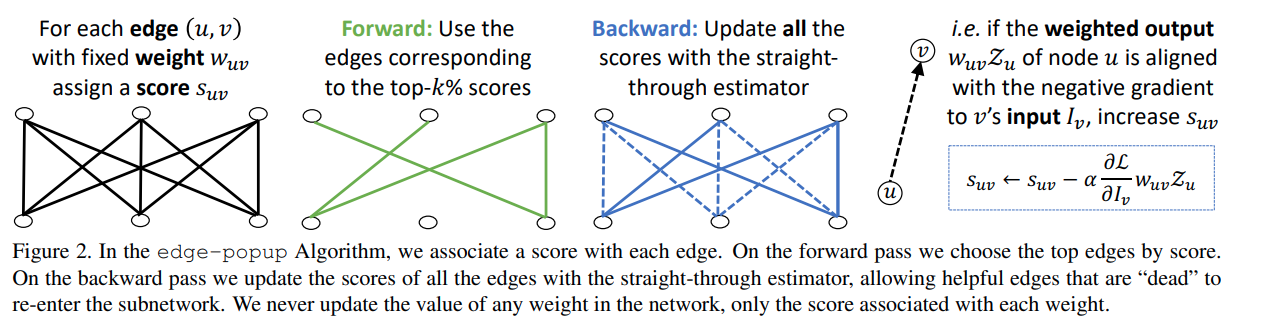
    Trong đó mỗi weight của chúng ta sẽ được đánh một giá trị popup score là một số thực dương. Việc lựa chọn các weight sẽ được sử dụng trong supermask đơn giản là lựa chọn top $k$ các popup score trên từng layer. Một câu hỏi đặt ra là làm sao để update score này. Chúng ta có thể tưởng tượng hai neuron $u$ và $v$ trong mạng nơ ron nối với nhau bằng một cạnh có giá trị là $W_{uv}$ tương ứng với nó là một score $S_{uv}$. Nếu score này được khởi tạo có giá trị thấp thì weight đó sẽ không được sử dụng trong quá trình forward pass. Tuy nhiên chúng ta vẫn có thể "bật" các weight này lên nếu như sau quá trình tối ưu score của nó được cập nhật cao lên.

    Hiểu một cách informal thì trong qúa trình back propagate chúng ta sẽ tìm cách cập nhật giá trị input của node $v$ sao cho nó làm minimize giá trị của hàm loss mà chúng ta đang xem xét. Thông thường, chúng ta sẽ cập nhật giá trị weight của node $u$ để output của nó có thể thoả mãn điều kiện tối ưu trên (negative gradient). Nhưng trong bài toán này chúng ta sẽ không thay đổi weight, thay vào đó chúng ta sẽ lựa chọn các node $u$ sao cho nó được aligned với negative gradient. Khi đó node $u$ chính là các node mà quá trình optimize chúng ta muốn tìm kiếm và có thể làm giảm hàm loss. Với mỗi cặp $u, v$ như vậy chúng ta sẽ đánh một điểm trọng số $s_{uv}$, trong mỗi quá trình optimize, thay vì cập nhật weight của từng node thì chúng ta sẽ cập nhật điểm của chúng. Nếu như một cạnh $u, v$ có số điểm dương liên tục trong suốt quá trình tối ưu thì nó sẽ được lựa chọn để đưa vào sub-network mà chúng ta cần tìm.

    Một cách tường minh hơn, chúng ta sẽ sử dụng các kí hiệu toán học để diễn tả thuật toán này. Kí hiệu $w_{uv}\mathcal{Z}_u$ là weighted output của neuran $u$ với $w_{uv}$ và $\mathcal{I}_v$ là đầu vào của neuron $v$. Chúng ta có thể cập nhật điểm số $s_{uv}$ với công thức sau:

    $$s_{uv} \leftarrow s_{uv} - \alpha \frac{\partial \mathcal{L}}{\partial \mathcal{I}_v}w_{uv}\mathcal{Z}_u$$

    Trong qúa trình forward chúng ta sử dụng top $k$% các cạnh có điểm score cao nhất tính theo magnitude làm các node trong sub-network. Thuật toán này được gọi là edge-popup. Chúng ta sẽ tìm hiểu chi tiết của thuật toán này trong phần tiếp theo sau đây

Chi tiết của thuật toán edge-popup

Đối với mạng Fully Connected network

    Đầu tiên chúng ta sẽ xem xét đối với mạng Fully Connected. Một mạng fully connected sẽ bao gồm nhiều layer kí hiệu từ $1....L$ trong đó tại layer thứ $l$ có $n_l$ node $V^{l}=\left \{ v_1^{l}, v_2^{l}, ..., v_{n_l}^{l} \right \}$. Chúng ta kí hiệu $\mathcal{I}_v$ là input của node $v$ và $\mathcal{Z}_v$ là output của nó. Trong đó chúng ta có $\mathcal{Z}_v = \sigma(\mathcal{I}_v)$ với $\sigma$ là một non-linear activation function (ví dụ ReLU). Đầu vào của neuron $v$ trong layer thứ $l$ được tính toán bằng tổng các weighted input từ layer ngay trước đó

    $$\mathcal{I}_v = \sum_{u \in V^{l-1}}w_{uv} \mathcal{Z}_u$$

    trong đó $w_{uv}$ là giá trị của tham số (weight) của layer thứ $l$. Trước khi training thường các weight này sẽ được khởi tạo bằng một phân phối (ví dụ phân phối chuẩn chẳng hạn). Về bản chất thuật toán edge-popup sẽ đi tìm ột sub-network hay có thể coi là một đồ thị con $\mathcal{G}=(\mathcal{V}, \mathcal{E})$. Lúc đó input node của $v$ trong layer thứ $l$ sẽ được tính bằng

    $$\mathcal{I}_v = \sum_{u, v \in \mathcal{E}}w_{uv} \mathcal{Z}_u$$

    Trong đó thì $\mathcal{E}$ là tập hợp các cạnh có chứa pop-up score cao nhất theo tỉ lệ $k\%$. Mỗi weight $w_{uv}$ trong mạng ban đầu có thể có học một popup score là $s_{uv}$. Công thức trên có thể được viết lại như sau:

    $$\mathcal{I}_v = \sum_{u \in \mathcal{V}^{l-1}}w_{uv} \mathcal{Z}_u h\left ( s_{uv} \right )$$

    trong đó $h\left ( s_{uv} \right ) = 1$ nếu như $s_{uv}$ nằm trong top $k\%$ các điểm cao nhất của layer $l$ và bằng 0 trong những trường hợp ngược lại. Điều đó dẫn đến một hiện tương đó là gradient của $h$ sẽ bằng 0 trong mọi trường hợp dẫn đến chúng ta không thể tính toán trực tiếp đạo hàm của hàm loss đối với $s_{uv}$. Thay vào đó chúng ta sẽ sử dụng straight-forward gradient được trình bày ở phần trên. Lúc này hàm $h$ sẽ được bỏ qua trong quá trình tính toán gradient và việc cập nhật của $s_{uv}$ sẽ được thực hiện như sau

    $$\hat{g}_{s_{u v}}=\frac{\partial \mathcal{L}}{\partial \mathcal{I}_{v}} \frac{\partial \mathcal{I}_{v}}{\partial s_{u v}}=\frac{\partial \mathcal{L}}{\partial \mathcal{I}_{v}} w_{u v} \mathcal{Z}_{u}$$

    trong đó $\mathcal{L}$ là hàm loss chúng ta cần minimize. Score $s_{uv}$ có thể update thông qua giải thuật SGD

    $$s_{uv} \leftarrow s_{uv} - \alpha \frac{\partial \mathcal{L}}{\partial \mathcal{I}_v}w_{uv}\mathcal{Z}_u$$

Implement thôi

    Trong paper này tác giả đã cung cấp sẵn code cho bài toán. Chúng ta có thể tham khảo tại đây. Ở đây mình sẽ chỉ giải thích một số hàm cơ bản trong implement của tác giả

Import thư viện cần thiết

import os
import math

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.optim.lr_scheduler import CosineAnnealingLR
import torch.autograd as autograd

Định nghĩa module GetSubNet

class GetSubnet(autograd.Function):
    @staticmethod
    def forward(ctx, scores, k):
        # Get the supermask by sorting the scores and using the top k%
        out = scores.clone()
        _, idx = scores.flatten().sort()
        j = int((1 - k) * scores.numel())

        # flat_out and out access the same memory.
        flat_out = out.flatten()
        flat_out[idx[:j]] = 0
        flat_out[idx[j:]] = 1

        return out

    @staticmethod
    def backward(ctx, g):
        # send the gradient g straight-through on the backward pass.
        return g, None

    Trong module này chungst asex thấy trong quá trình forward thì hàm GetSSubNet sẽ thực hiện lấy top K% những weight có score cao nhất của layer. Lưu ý rằng những cạnh nào có score được chọn sẽ nhận giá trị 1 ngược lại những score dưới ngưỡng sẽ nhận giá trị 0. Trong implement trên chúng ta để ý flat_out và out share chung một địa chỉ trên memory do tính chất của mutable object trong Python. Trong hàm backward thì gradient được truyền trực tiếp qua layer mà bỏ qua hàm lấy top K trong forward.

Định nghĩa layer SuperMaskConv

class SupermaskConv(nn.Conv2d):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)

        # initialize the scores
        self.scores = nn.Parameter(torch.Tensor(self.weight.size()))
        nn.init.kaiming_uniform_(self.scores, a=math.sqrt(5))

        # NOTE: initialize the weights like this.
        nn.init.kaiming_normal_(self.weight, mode="fan_in", nonlinearity="relu")

        # NOTE: turn the gradient on the weights off
        self.weight.requires_grad = False

    def forward(self, x):
        subnet = GetSubnet.apply(self.scores.abs(), sparsity)
        w = self.weight * subnet
        x = F.conv2d(
            x, w, self.bias, self.stride, self.padding, self.dilation, self.groups
        )
        
        return x

    Trong hàm này chúng ta sẽ extend từ class nn.Conv2d để định nghĩa lại các xử lý trong layer này. Các thay đổi chính của chúng ta như sau:

• Khởi tạo các weight bằng kaiming_normal_ và score bằng kaiming_uniform_. Bạn đọc lưu ý đặt random_seed cho PyTorch để kết quả ở mỗi lần khởi tạo là giống nhau
• Định nghĩa một lớp supermask gọi là scores để lưu trữ điểm $s_{uv}$ của thuật toán edge-popup. Đây có thể coi là một mảng nhị phận biểu diễn vị trí các node được sử dụng
• Weight được sử dụng sẽ là kết quả dot product của weight của layer và supermask score qua phần w = self.weight * subnet
• Sau đó phép tính tích chập sẽ được tính toán dựa trên weight mới

Định nghĩa layer SupermaskLinear

class SupermaskLinear(nn.Linear):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)

        # initialize the scores
        self.scores = nn.Parameter(torch.Tensor(self.weight.size()))
        nn.init.kaiming_uniform_(self.scores, a=math.sqrt(5))

        # NOTE: initialize the weights like this.
        nn.init.kaiming_normal_(self.weight, mode="fan_in", nonlinearity="relu")

        # NOTE: turn the gradient on the weights off
        self.weight.requires_grad = False

    def forward(self, x):
        subnet = GetSubnet.apply(self.scores.abs(), sparsity)
        w = self.weight * subnet
        
        return F.linear(x, w, self.bias)

    Các phần thực hiện tương tự như đối với phép Conv2D nhưng cho lớp Fully connected nn.Linear

Định nghĩa kiến trúc mạng

    Chúng ta tiến hành định nghĩa kiến trúc mạng LeNet thông qua các layer được định nghĩa phía trên. Về cơ bản nó không khác gì các mạng LeNet thông thường

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = SupermaskConv(1, 32, 3, 1, bias=False)
        self.conv2 = SupermaskConv(32, 64, 3, 1, bias=False)
        self.dropout1 = nn.Dropout2d(0.25)
        self.dropout2 = nn.Dropout2d(0.5)
        self.fc1 = SupermaskLinear(9216, 128, bias=False)
        self.fc2 = SupermaskLinear(128, 10, bias=False)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.max_pool2d(x, 2)
        x = self.dropout1(x)
        x = torch.flatten(x, 1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.dropout2(x)
        x = self.fc2(x)
        output = F.log_softmax(x, dim=1)
        
        return output

Định nghĩa hàm train và test

    Hàm train model

def train(model, device, train_loader, optimizer, criterion, epoch):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))

    Hàm test model

def test(model, device, criterion, test_loader):
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += criterion(output, target)
            pred = output.argmax(dim=1, keepdim=True)  # get the index of the max log-probability
            correct += pred.eq(target.view_as(pred)).sum().item()

    test_loss /= len(test_loader.dataset)

    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

Định nghĩa các hyper parameters

batch_size = 64
momentum = 0.9
wd = 0.0005
lr = 0.01
epochs = 20
sparsity = 0.5
log_interval = 1000
seed = 2021

Định nghĩa dataset MNIST

use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST(
        os.path.join("./data", "mnist"),
        train=True,
        download=True,
        transform=transforms.Compose(
            [transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]
        ),
    ),
    batch_size=batch_size,
    shuffle=True
)

test_loader = torch.utils.data.DataLoader(
    datasets.MNIST(
        os.path.join("./data", "mnist"),
        train=False,
        transform=transforms.Compose(
            [transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]
        ),
    ),
    batch_size=batch_size,
    shuffle=True
)

Huấn luyến mô hình

model = Net().to(device)

optimizer = optim.SGD(
    [p for p in model.parameters() if p.requires_grad],
    lr=lr,
    momentum=momentum,
    weight_decay=wd,
)

criterion = nn.CrossEntropyLoss().to(device)

scheduler = CosineAnnealingLR(optimizer, T_max=epochs)

for epoch in range(1, epochs + 1):
    train(model, device, train_loader, optimizer, criterion, epoch)
    test(model, device, criterion, test_loader)
    scheduler.step()

torch.save(model.state_dict(), "mnist_cnn.pt")

    Chúng ta thu được kết quả như sau:

Train Epoch: 1 [0/60000 (0%)]	Loss: 2.541810

Test set: Average loss: 0.0038, Accuracy: 9279/10000 (93%)

Train Epoch: 2 [0/60000 (0%)]	Loss: 0.390082

Test set: Average loss: 0.0028, Accuracy: 9477/10000 (95%)

Train Epoch: 3 [0/60000 (0%)]	Loss: 0.249726

Test set: Average loss: 0.0022, Accuracy: 9593/10000 (96%)

Train Epoch: 4 [0/60000 (0%)]	Loss: 0.270498

Test set: Average loss: 0.0020, Accuracy: 9599/10000 (96%)

Train Epoch: 5 [0/60000 (0%)]	Loss: 0.207395

Test set: Average loss: 0.0018, Accuracy: 9669/10000 (97%)

Train Epoch: 6 [0/60000 (0%)]	Loss: 0.488036

Test set: Average loss: 0.0015, Accuracy: 9709/10000 (97%)

Train Epoch: 7 [0/60000 (0%)]	Loss: 0.170290

Test set: Average loss: 0.0013, Accuracy: 9731/10000 (97%)

Train Epoch: 8 [0/60000 (0%)]	Loss: 0.282664

Test set: Average loss: 0.0012, Accuracy: 9753/10000 (98%)

Train Epoch: 9 [0/60000 (0%)]	Loss: 0.241693

Test set: Average loss: 0.0012, Accuracy: 9763/10000 (98%)

Train Epoch: 10 [0/60000 (0%)]	Loss: 0.344497

Test set: Average loss: 0.0011, Accuracy: 9778/10000 (98%)

Train Epoch: 11 [0/60000 (0%)]	Loss: 0.143159

Test set: Average loss: 0.0011, Accuracy: 9792/10000 (98%)

Train Epoch: 12 [0/60000 (0%)]	Loss: 0.218363

Test set: Average loss: 0.0010, Accuracy: 9798/10000 (98%)

Train Epoch: 13 [0/60000 (0%)]	Loss: 0.164655

Test set: Average loss: 0.0009, Accuracy: 9805/10000 (98%)

Train Epoch: 14 [0/60000 (0%)]	Loss: 0.125553

Test set: Average loss: 0.0009, Accuracy: 9801/10000 (98%)

Train Epoch: 15 [0/60000 (0%)]	Loss: 0.170433

Test set: Average loss: 0.0009, Accuracy: 9807/10000 (98%)

Train Epoch: 16 [0/60000 (0%)]	Loss: 0.032195

Test set: Average loss: 0.0009, Accuracy: 9809/10000 (98%)

Train Epoch: 17 [0/60000 (0%)]	Loss: 0.062252

Test set: Average loss: 0.0010, Accuracy: 9802/10000 (98%)

Train Epoch: 18 [0/60000 (0%)]	Loss: 0.073142

Test set: Average loss: 0.0009, Accuracy: 9807/10000 (98%)

Train Epoch: 19 [0/60000 (0%)]	Loss: 0.228540

Test set: Average loss: 0.0009, Accuracy: 9807/10000 (98%)

Train Epoch: 20 [0/60000 (0%)]	Loss: 0.131782

Test set: Average loss: 0.0009, Accuracy: 9828/10000 (98%)

    Bạn đọc có thể training thêm nhiều epoch hơn để thấy được hiệu quả của mạng. Chúng ta có thể thấy rằng không cần training weight mà chỉ cần tìm subnetwork cũng có thể cho độ chính xác tốt trên tập dữ liệu MNIST.

Thảo luận

Điểm tốt

• Paper đêm đến một giả thuyết mới về việc có tồn tại hay không một sub-network trong một mạng nơ ron được khởi tạo ngẫu nhiên mà chỉ với sub-network đó cũng có thể đáp ứng được độ chính xác của bài toán
• Paper đưa ra phương pháp huấn luyện để tim ra sub-network sử dụng giải thuật edge-popup
• Kết quả đưa ra khá nhiều hứa hẹn khi một sub-network của ResNet-50 thể đạt được tương đương với việc train từ đầu mạng ResNet-34 trên tập ImageNet

Điểm còn hạn chế

• Chưa so sánh được hiệu năng và thời gian giữa việc training model từ đầu và việc tìm subnetwork. Phần này thiết nghĩ là rất quan trọng để có thể áp dụng trong các dự án thực.
• Chưa có lý thuyết rõ ràng về việc định nghĩa original network tương ứng với từng tập dataset. Cách chọn original network như thế nào để sub-network có độ chính xác tốt nhất.
• Chưa áp dụng thử được cho nhiều loại dữ liệu khác nhau cũng như nhiều bài toán khác nhau (Object Detect, Segmentation)