Tree hay Binary Tree đều là những khái niệm quen thuộc đối với dev chúng ta hiện nay. Nên bài viết này mình sẽ không focus nhiều vào lý thuyết về tree, mà sẽ cùng với các bạn tìm hiểu về chúng được sử dụng trong Python như thế nào. Trước khi bắt đầu, mình sẽ nói qua về 2 khái niệm này để cùng nhau ôn lại kiến thức nha.

Tree

    Là cấu trúc dữ liệu phi tuyến tính (non-linear) đại diện cho các nút (node) được kết nối với nhau bởi các cạnh (edges). Mỗi cây đều bao gồm 1 nút cha (parent node), các nút trái và nút phải là các nút con (children nodes)

Binary Tree

    Một tree mà bao gồm nhiều nhất một phần tử con ở mỗi bên trái và phải được gọi là Cây nhị phân (Binary Tree). Mỗi phần tử con chỉ có thể có hai phần tử con. Nút con bên trái có giá trị nhỏ hơn, nút con bên phải có giá trị lớn hơn giá trị của nút cha.

Implement a Binary Tree

    Bài toán: Nhập một số bất kỳ và thêm chúng vào Cây nhị phân.

1. Lên kịch bản

1.1. Xác định Parent node

    Ở đây mình chọn một con số mà đa số các anh em đều thích đó là con số 69 làm gốc. Ta sẽ có một cây nhị phân có dạng.

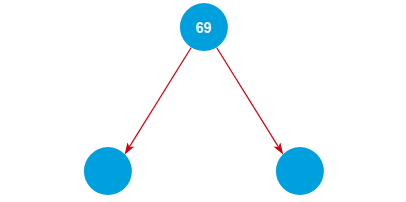
1.2. Thêm các chữ số vào cây

    Sau đó, mình sẽ tiếp tục thêm 2 số 39 và 79. Theo quy tắc "Nhỏ trái - Lớn phải" thì mình có thể dễ dàng thêm 2 số này vào cây. Và cây của chúng ta giờ đây trông đã hoàn chỉnh hơn rồi.

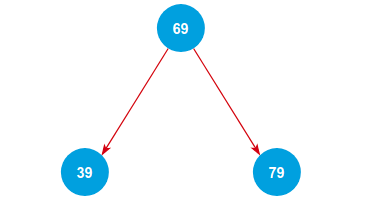
    Để chiếc cây trông đẹp hơn thì mình cùng thêm vào lần lượt các số: 68, 75, 30, 80.
Ở đây, chúng ta có một vấn đề nho nhỏ với con số 68 này. Chúng ta thấy rằng 68 lớn hơn 39 nhưng 68 cũng nhỏ hơn 79. Vậy, chúng ta sẽ đặt nó ở đâu được?
Để ý kỹ hơn một chút ta thấy có thể thấy 68 < 69 (Parent Node) nên theo quy tắc, ta sẽ để nó ở bên nhỏ hơn (39). Với số tiếp theo 75 cũng tương tự ta sẽ đặt nó ở vế nhỏ hơn của 79. Cuối cùng, ta được cây nhị phân trông khá bắt mắt =))

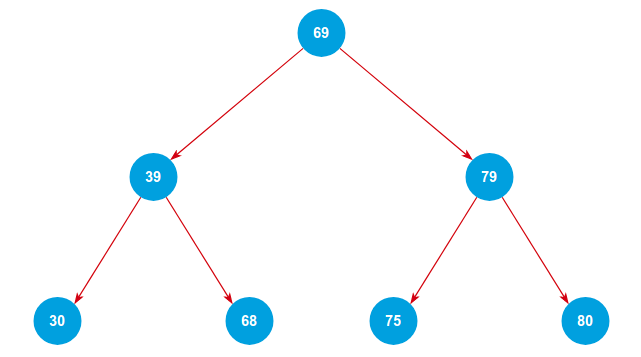
    Khi chuyển về dạng dãy số thì chúng ta sẽ lấy các chữ số từ trái qua phải hay nói cách khác, cây nhị phân thể hiện cho dãy số được sắp xếp từ nhỏ đến lớn.

Output: 30, 39, 68, 69, 75, 79, 80

    Đây chỉ là bản "phác thảo" ý tưởng trên giấy. Vậy còn khi viết thành code nó sẽ ra sao? Chúng ta cùng tìm hiểu tiếp nha.

1.3. Tìm kiếm phần tử trong cây nhị phân

    Để tìm kiếm được, ta lấy Parent Node làm gốc để so sánh. Nếu số nhận vào lớn hơn gốc, số cần tìm sẽ nằm ở bên phải của gốc và ngược lại, nếu nhỏ hơn số cần tìm sẽ nằm ở bên trái. Tương tự, chúng ta lấy nút con tiếp theo làm gốc và tiếp tục tìm kiếm. Kết quả cuối cùng sẽ nhận được là tìm thấy hoặc không.
Lợi ích của việc tìm kiếm bằng cây nhị phân giúp chúng ta không cần phải focus vào nửa còn lại của Parent Node, giúp giảm thời gian đáng kể khi tìm kiếm với lượng dữ liệu lớn.

2. Chuyển thể thành "phim"

    Sau khi đã được lên được "Kịch bản" thì tiếp theo chúng ta cùng chuyển thể nó thành "phim" nhé (dull)

2.1. Xác định Parent node

class Node:
    def __init__(self, data):
        self.left_child = None
        self.right_child = None
        self.parent_node = data

    def print_tree(self):
        print(self.data)


root = Node(69)

root.print_tree()

    Ở đây mình tạo một class Node và gán một giá trị được nhập từ bàn phím cho nút.

# Output
69

2.2. Thêm các chữ số vào cây

class Node:
    def __init__(self, data):
        self.left_child = None
        self.right_child = None
        self.parent_node = data

    # print function
    def print_tree(self):
        # if there is no left_child then don't print
        if self.left_child:
            self.left_child.print_tree()

        # print parent_node at the center
        print(self.parent_node)

        # if there is no right_child then don't print
        if self.right_child:
            self.right_child.print_tree()

    def insert_number(self, input_number):
        # Compare the new value with the parent node
        if self.parent_node:
            # if input number less than parent node, then it is on the left
            if input_number < self.parent_node:
                if self.left_child is None:
                    self.left_child = Node(input_number)
                else:
                    self.left_child.insert_number(input_number)

            # if input number greater than parent node, then it is on the right
            elif input_number > self.parent_node:
                if self.right_child is None:
                    self.right_child = Node(input_number)
                else:
                    self.right_child.insert_number(input_number)
        else:
            self.parent_node = input_number


root = Node(69)
root.insert_number(39)
root.insert_number(79)
root.insert_number(68)
root.insert_number(75)
root.insert_number(30)
root.insert_number(80)

root.print_tree()

    Chúng ta sẽ được kết quả:

# Output
30
39
68
69
75
79
80

2.3. Tìm kiếm phần tử trong cây nhị phân

class Node:
    def __init__(self, data):
        ...

    def print_tree(self):
        ...

    def insert_number(self, input_number):
        ...

    # find_value method to compare the value with nodes
    def find_value(self, input_number):
        if input_number < self.parent_node:
            if self.left_child is None:
                return str(input_number)+" is not Found"
            return self.left_child.find_value(input_number)
            
        elif input_number > self.parent_node:
            if self.right_child is None:
                return str(input_number)+" is not found"
            return self.right_child.find_value(input_number)
            
        else:
            return str(self.parent_node) + " is found"
            
root = Node(69)
root.insert_number(39)
root.insert_number(79)
root.insert_number(68)
root.insert_number(75)
root.insert_number(30)
root.insert_number(80)

print(root.find_value(75))
print(root.find_value(70))

    Kết quả nhận được là:

# Output
75 is found
70 is not found

Lời cảm ơn

    Nếu thấy "bộ phim" này có ích, đừng ngần ngại cho mình 1 upvote mình có thêm động lực ra nhiều bài viết có ích hơn nữa. Nếu "bộ phim" này có điều gì chưa được, hãy comment phía dưới để mình cải thiện thêm nha
Cảm ơn các bạn rất nhiều