Giới thiệu về cây tìm kiếm ưu tiên (Priority Search Tree) và cấu trúc dữ liệu liên quan

Giới thiệu

Trong khoa học máy tính, cây tìm kiếm ưu tiên (priority search tree) là một cấu trúc dữ liệu dạng cây để lưu trữ các điểm trong không gian hai chiều (Oxy). Ban đầu cây tìm kiếm ưu tiên được giới thiệu bởi Edward McCreight năm 1985. Ban đầu cây tìm kiếm ưu tiên là sự mở rộng của hàng đợi ưu tiên (priority queue) với mục đích cải thiện thời gian tìm kiếm từ: $O(n)$ đến $O$ ( $s$ + $log n$ ) trong đó n là số điểm trong cây và s là số trong tổng số điểm được trả về bởi tìm kiếm. Sau đó, cây tìm kiếm ưu tiên được sử dụng để lưu trữ một tập hợp các điểm 2 chiều được sắp xếp theo mức độ ưu tiên(priority) và theo một giá trị khóa (key value). Điều này được thực hiện bằng cách tạo kết hợp giữa hàng đợi ưu tiên (priority queue) và cây tìm kiếm nhị phân (binary search tree). Kết quả là một cây trong đó mỗi nút đại diện cho một điểm trong tập dữ liệu gốc. Điểm được chứa bởi nút là điểm có mức độ ưu tiên thấp nhất. Ngoài ra, mỗi nút còn chứa một giá trị khóa dùng để chia các điểm còn lại (thường là trung vị của các khóa, không kể điểm của nút) thành cây con trái và phải. Các điểm được chia bằng cách so sánh các giá trị khóa của chúng với khóa nút, ủy nhiệm các giá trị có khóa thấp hơn cho cây con bên trái và các giá trị lớn hơn cho cây con bên phải.

Hình 1: Ví dụ về cây tìm kiếm ưu tiên:

Cách xây dựng cây PST

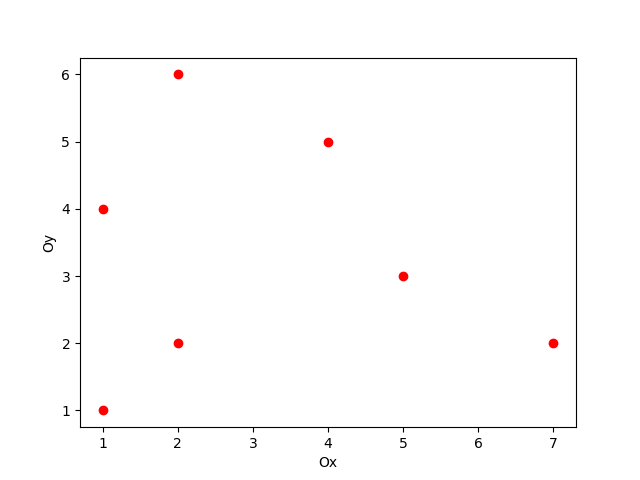
Cây tìm kiếm ưu tiên là một cấu trúc dữ liệu lưu trữ các điểm trên không gian 2 chiều. Đầu tiên, chúng ta xem xét n các điểm trên cùng một mặt phẳng, mỗi điểm đều có tọa độ x và tọa độ y biểu diễn trên hình 2. Bài toán xây dựng cây tìm kiếm ưu tiên được mô tả như sau:

Đầu vào: Ta có n điểm thuộc mặt phẳng $S$ = { $p_{i}$ │ $i=1,2,3…n$ } và các điểm $p_i (p_i.x, p_i.y)$ .

Đầu ra: Cây tìm kiếm ưu tiên lưu trữ các điểm trong không gian 2 chiều.

Trình tự:

Nếu S = NULL thì trả về NULL.
Tìm điểm $p_{i}$ có tọa độ y là nhỏ nhất đặt làm root (gốc), $p_{i}$ = min ⁡{ $p_{i}$ .y ∊S }
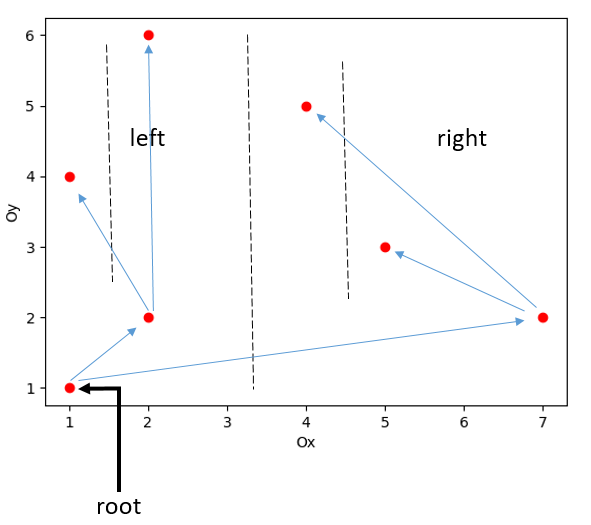
Tìm đường trung tuyến (median) chia đôi các điểm về 2 phía trái và phải. Ở phía bên trái tìm điểm $p_{i}$ = min⁡ { $p_{i}$ .y ∊ $S_l$ \ { $p_{parent}$ } } gán làm con của nút cha ở bước 2, thực hiện tương tự với phía bên phải xem hình 3.
Đệ quy lại PST(s) với phía bên trái.
Đệ quy lại PST(s) với phái bên phải.
Kết thúc.

Hình 2: Biểu diễn các điểm trên mặt phẳng Oxy

Hình 3: Mô tả xác dựng cây PST

Mã giải được viết bằng pascal:

procedure construct_PST(RPSTPtr):
    CONST
        k = 30000, FirstKey = 0, LastKey = k - 1;
        FirstNonKey = LastKey + 1;
    TYPE
        KeyRange First_Key… Last_Key;
        KeyBound First_Key… FirstNonKey;
        Pair= RECORD x, y: KeyRange END;
        RPSTPtr = RPST;
        RPST=RECORD
            p: Pair;
            left, right: RPSTPtr
            END;

Thêm nút mới vào cây

Kế tiếp, cũng đến với vấn đề thêm một nút mới vào cây. Giả sử có một nút mới với tọa độ $x_{new}$ và $y_{new}$ cần phải thêm vào cây. Như vậy sẽ cần tính toán lại xem có sự thay đổi ở gốc cây (root) và các đường trung tuyến (median). Sau đó sẽ so sánh xem nút mới có thể chèn vào gốc cây hoặc là các nút ở phía bên trái, phải.

Mã giải pascal thêm nút mới vào cây:

PROCEDURE InsertPair(VAR t: RPSTPtr; newPr: Pair;
	lowerX: KeyRange; upperX: KeyBound);
	VAR
		p: Pair;
		middleX: KeyRange
	BEGIN
	IF t NIL THEN
		BEGIN
		NEW(t);  (* tao nut tren cay *)
		t.p := newPr;
		t.left := NIL;
		t.right := NIL;
		END
	ELSE IF t.p.x <> newPr.x (* gia su bien x la du nhat *)
		THEN
		BEGIN
		IF newPr.y < t.p.y THEN (* neu y_new < y_old *)
			BEGIN p := t.p; t.p := newPr END
			(*tao nut moi*)
		ELSE p := newPr;
			middleX := (lowerX+upperX) DIV 2;
			IF p.x < middleX
			THEN InsertPair(t.left, p, lowerX, middleX)
			ELSE InsertPair(t.right, p, middleX, upperX);
		END; (* neu nut da ton tai thi khong them *)
	END; (* ket thuc ")

Xóa nút ở trên cây

Kế tiếp, cũng đến với vấn đề thêm một nút mới vào cây. Giả sử có một nút cũ với tọa độ $x_{old}$ và $y_{old}$ cần phải xóa khỏi cây. Như vậy sẽ cần tính toán lại xem có sự thay đổi ở gốc cây, các nút cha, các đường trung tuyến (median) và cập nhập lại cây.

Mã giải pascal xóa một nút ở trên cây:

PROCEDURE DeletePair(VAR t: RPSTPtr; oldPr: Pair;
	lowerX: KeyRange; upperX: KeyBound);
	VAR
		middleX: KeyRange
	BEGIN
	IF t <> NULL THEN
		BEGIN
		IF t.p.x == oldPr.x (* co duy nhat 1 bien x *)
			THEN
			BEGIN (* tim vi tri can xoa *)
			IF t.left <> NULL THEN
				BEGIN
				IF t.right <> NULL THEN
					BEGIN (* nut o ben trai hoac ben phai cua cay con *)
					IF t.left.p.y < t.right.p.y THEN
						BEGIN (* nut o ben trai *)
						t.p := t.left.p;
						DeletePai r( t.left, t.p, lowerX, upperX);
						END
					ELSE
						BEGIN (* nut o ben phai *)
						t.p := t.right.p;
						DeletePair(t.right, t.p, lowerX, upperX);
						END;
					END
				ELSE
					BEGIN (* nut chi o ben trai *)
					t.p := t.left.p;
					DeletePair(t.left, t.p, lowerX, upperX);
				END;
			END
		ELSE
			BEGIN
			IF t.right <> NULL THEN
				BEGIN (* nut chi o ben phai *)
				t.p := t.right.p;
				DeletePair(t.right, t.p, lowerX, upperX);
			END
			ELSE
				BEGIN (* nut khong co cay con *)
				DISPOSE(t);
				t := NIL;
				END;
			END;
		END
	ELSE
		BEGIN (* xoa nut khoi cay con *)
		middleX := (lowerX+upperX) DIV 2;
		IF oldPr.x < middleX
			THEN DeletePair(t.left, oldPr, lowerX, middleX)
			ELSE DeletePair(t.right, oldPr, middleX, upperX);
		END;
	END; (* ELSE nut này khong co trong cay nen khong the xoa *)
	END; (* ket thuc *)
	TYPE CondPair RECORD
		valid: BOOLEAN;
		p: Pair;
		END;

Truy vấn các điểm trên cây

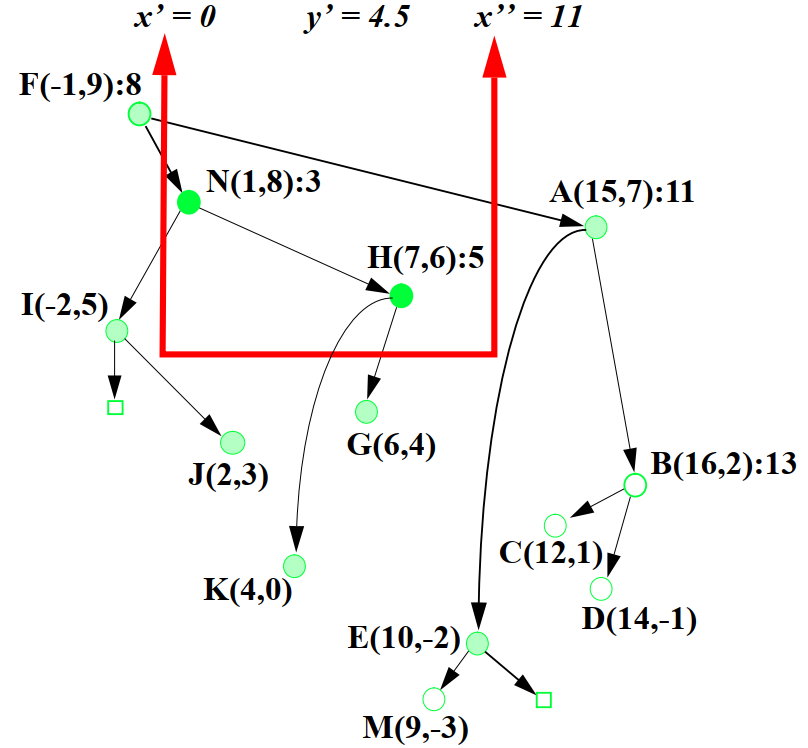
Tiếp theo, hãy xem xét vấn đề tìm kiếm trên cây. Cây tìm kiếm ưu tiên có thể giúp tìm kiếm các điểm thỏa mãn các điều kiện trên mặt phẳng Oxy, điều đó khác so với cây tìm kiếm nhị phân (BST) là chỉ tìm kiếm 1 điểm trên cây. Khi tìm kiếm ta cần xác định được phạm vi tìm kiếm dưới dạng hình chữ nhật có giới hạn $x_{min}$ và $x_{max}$ và độ ưu tiên y. Trong hình dưới đây hãy xem xét vấn đề tìm kiếm các điểm trên cây tìm kiếm ưu tiên với $y_{max}$ làm gốc.

Hình 4: Mô tả phạm vi tìm kiếm

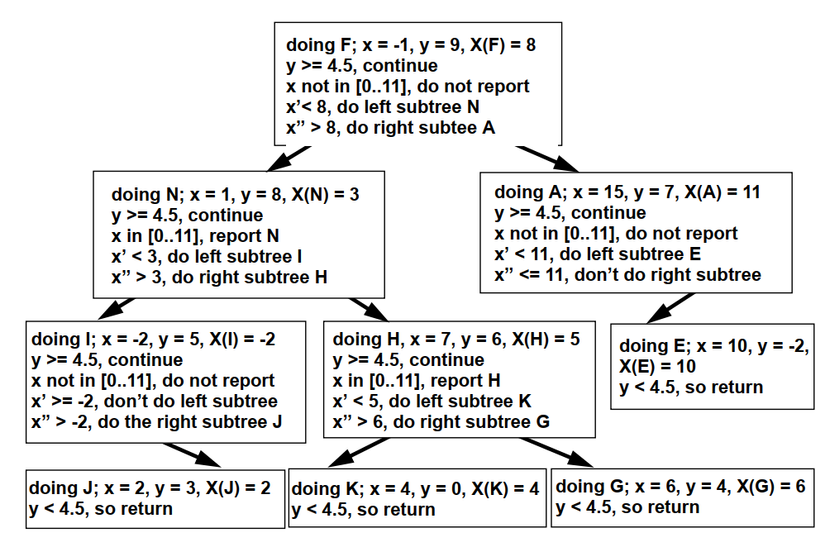
Hình 5: Mô tả phương pháp tìm kiếm

Mã giải pascal thuật toán tìm kiếm:

procedure PST( tree, x_min, x_max, y_p):
	IF tree <> NULL THEN
		IF y_p > tree.node.y THEN
			IF tree.node.x >= x_min AND tree.node.x <= x_max
                THEN report tree.node;
			IF x_min < tree.node.middleX THEN
				PST(tree.left, x_min, x_max, y_p);
			IF x_max > tree.node.middleX THEN
				PST(tree.left, x_min, x_max, y_p);
		ELSE END;
	ELSE END;

Thuật toán triển khai với Python:

def query_priority_search_tree(tree, x_min, x_max, y_priority):
    if tree is None:
        return
    if y_priority < tree.node.y:
        return
    if tree.node.x in range(x_min, x_max + 1):
        result_query.append(tree.node.name)
    if x_min < tree.node.middleX:
        query_priority_search_tree(tree.left, x_min, x_max, y_priority)  # tim ben trai
    if x_max > tree.node.middleX:
        query_priority_search_tree(tree.right, x_min, x_max, y_priority)  # tim ben phai

Bài toán tìm kiếm điểm có y nhỏ nhất

Bài toán đưa ra vấn đề đó là tìm kiếm một điểm có tọa độ y nhỏ nhất trong một phạm vi hình chữ nhật cho trước trên mặt phẳng Oxy. Bằng mắt thường có thể thấy ngay điểm cần tìm trong phạm vị với số lượng ít các điểm trên mặt phẳng. Nếu tìm tuần tự so sánh từng điểm với nhau thì độ phức tạp của thuật toán sẽ là $O(n)$ . Vì thế ta sử dụng cấu trúc dữ liệu cây tìm kiếm ưu tiên để thực hiện việc tìm kiếm với độ phức tạp từ $O(n)$ đến $O$ ( $s$ + $log n$ ).

Mã giải thuật toán:

FUNCTION MinYlnXRange(t: RPSTPtr; xO, xl: KeyRange;
	lowerX: KeyRange; upperX: KeyBound): CondPair;
	VAR
		c, cRight: CondPair;
		middleX: KeyRange
	BEGIN
	IF t <> NIL THEN
		IF (xO <= t.p.x) AND (t.p.x <= xl) THEN
		(" pham vi tim kiem ")
			BEGIN
			c.valid := TRUE;
			c.p := t.p;
			END
		ELSE
			BEGIN
			middleX := (lowerX+upperX) DIV 2;
			IF xO < middleX THEN 
				c := MinYlnXRange(t.left, xO, xl, lowerX, middleX)
			ELSE c.valid := FALSE;
			IF middleX <= xl THEN 
				cRight := MinYlnXRange(t.right, xO, xl, middleX, upperX)
			ELSE cRight.valid := FALSE;
			IF NOT c.valid OR (cRight.valid AND (cRight.p.y < c.p.y)) THEN
				c := cRight;
			END
	ELSE c.valid := FALSE; (" cay con rong ")
	MinYInXRange := c;
	END: (" ket thuc ")

Bài toán tìm điểm có x lớn nhất

Bài toán đưa ra vấn đề đó là tìm kiếm một điểm có tọa độ x lớn nhất trong một phạm vi hình chữ nhật cho trước trên mặt phẳng Oxy. Bằng mắt thường có thể thấy ngay điểm cần tìm trong phạm vị với số lượng ít các điểm trên mặt phẳng. Nếu tìm tuần tự so sánh từng điểm với nhau thì độ phức tạp của thuật toán sẽ là $O(n)$ . Vì thế ta sử dụng cấu trúc dữ liệu cây tìm kiếm ưu tiên để thực hiện việc tìm kiếm với độ phức tạp từ $O(n)$ đến $O$ ( $s$ + $log n$ ).

Mã giải thuật toán:

FUNCTION MaxXlnRectangle(t: RPSTPtr; xO, xl, yl: KeyRange;
	lowerX: KeyRange; upperX: KeyBound): CondPair;
	VAR
		c: CondPai r;
		middleX: KeyRange
	BEGIN
		IF t <> NIL THEN
			BEGIN
			IF t.p.y > yl THEN
				(* Khong co nut nao trong cay con nay nam trong tim kiem *)
				c.valid := FALSE
			ELSE
				BEGIN
				middleX := (lowerX+upperX) DIV 2;
				IF middleX < xl THEN
				(* ket qua chi o cay con phai*)
					c := MaxXInRectangle(t.right, xO, xl, yl,
					middleX, upperX)
				ELSE c.valid := FALSE;
				
				IF (NOT c.valid) AND (xO <= middleX) THEN
				(* ket qua chi o cay con trai *)
					c := MaxXlnRectangle(t.left, xO, xl, yl,
					lowerX, middleX);
		
				IF (xO <= t.p.x) AND (t.p.x <= xl) AND
				((NOT c.valid) OR (c.p.x < t.p.x)) THEN
				(* t.p is best of all in the search rectangle *)
					BEGIN
					c.valid := TRUE;
					c.p := t,.p;
					END;
				END
			END
		ELSE c.valid := FALSE; (* cay con rong *)
		MaxXInRectangle := c;
		END; (* ket thuc *)

Tải về mã nguồn

Xem toàn bộ source code bằng python tại github

Tham khảo

[1] McCreight, Edward (May 1985). “Priority search trees”. SIAM Journal on Scientific Computing.

[2] D.T. Lee. “Interval, Range, and Priority Search Tree”. Academia Sinica.

[3] Dina Q Goldin Karon (March 8, 1993). “Priority Search Tree”. Computational Geometry.