Ở bài viết này, chúng ta bắt đầu một thực hiện một trình phân tích cú pháp thực sự - với một khả năng xử lí lỗi tốt, cấu trúc mạch lạc.
Nó không khó như bạn nghĩ, vì chúng ta đã tiếp thu rất nhiều kiến thức khó ở bài viết trước. Bạn đã biết cách sử dụng biểu thức để biểu diễn cú pháp. Bạn đã quen với cây cú pháp và chúng ta có một số đối tượng biểu thức trong Dart để đại diện cho chúng. Phần còn lại chúng ta phải thực hiện là phân tích - đổi từ các token sang cây cú pháp.
"Trò chơi" phân tích cú pháp
Ở bài viết trước, chúng ta đã lấy một cây cú pháp và biến đổi chúng thành một chuỗi đại diện qua AstPrinter. Parser làm điều ngược lại, lấy từ chuỗi Token và cố gắng phân tích nó ra dạng cây cú pháp nhưng đôi khi chiều ngược lại sẽ gây sự khó hiểu cho trình phân tích cú pháp.
Sự bất đồng trong phân tích cú pháp
Sự bất đồng ở đây có nghĩa là trình phân tích cú pháp có thể hiểu sai mã của lập trình viên. Khi phân tích cú pháp, chúng ta không chỉ xác định xem chuỗi có phải là mã ViL hợp lệ hay không, mà còn phải thực hiện kiểm tra các token nào khớp với biểu thức nào. Đây là bộ quy tắc của ViL ta thiết lập bài trước:
expression => literal
| unary
| binary
| grouping ;
literal => số | chuỗi | "đúng" | "sai" | "rỗng" ;
grouping => "(" expression ")" ;
unary => ( "-" | "!" ) expression ;
binary => expression operator expression ;
operator => "==" | "!=" | "<" | "<=" | ">" | ">=
| "+" | "-" | "*" | "/" ;
Đây là một chuỗi hợp lệ so với bảng quy tắc trên:

Source: https://craftinginterpreters.com
Với chuỗi này ta có hai cách phân tích sau, cách một như sau:
- Bắt đầu từ
expressionta chọnbinary - Với vế trái của
binarychọnliteralvới giá trị số là6 - Toán tử của
binarychọn/ - Vế phải, tiếp tục chọn
binary, phân tích tiếp - Phân tích đến cùng biểu thức
binaryta có vế trái toán tử vế phải tương ứng3 - 1
Cách còn lại là:
- Bắt đầu từ
expressionta chọnbinary - Với vế trái của
binarychọnliteralvới giá trị số là6 - Toán tử của
binarychọn/ - Vế phải ta lấy số
3 - Gom cả
binaryvừa phân tích thành vế trái củabinarylớn hơn với toán tử là-và vế phải là1
Chúng tạo ra chuỗi giống nhau, nhưng không phải cây cú pháp giống nhau:
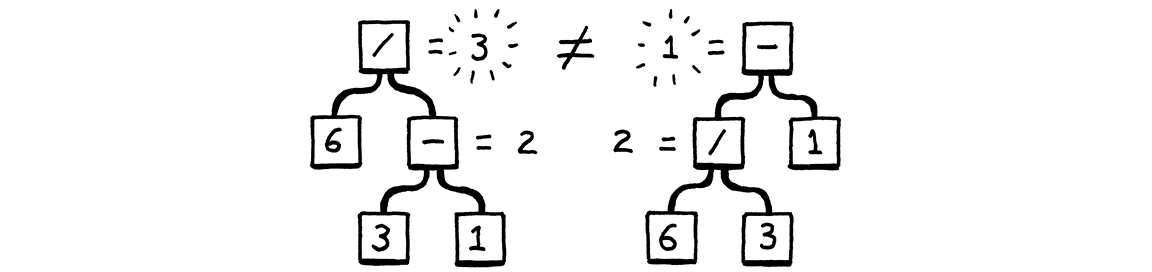
Nói cách khác thì cách một là cây phân tích của chuỗi 6 / (3 - 1), cách hai là cây phân tích của chuỗi (6 / 3) - 1. Quy tắc binary tức biểu thức hai vế cho phép chúng ta lồng các biểu thức khác vào với nhau bao nhiêu tùy ý. Điều đó ảnh hưởng đến kết quả tính toán. Toán học giải quyết điều này bằng cách định nghĩa quy tắc về sự ưu tiên và sự liên kết, ViL cũng vậy.
Quy tắc xử lí sự bất đồng
- Sự ưu tiên Xác định toán tử nào được xử lí trước. Ưu tiên xử lí phép chia trước phép trừ trong ví dụ trên. Toán tử mức độ ưu tiên cao hơn xử lí sớm hơn toán tử mức độ ưu tiên ít hơn.
- Sự liên kết Xác định toán tử nào được tính toán đầu tiên trong một loại các toán tử giống nhau. Tức là ưu tiên tính từ trái qua phải hay phải qua trái trước. Toán tử
-là loại ưu tiên từ trái qua phải trước tức một biểu thức dạng:
7 - 5 - 3
// Tương đương với biểu thức:
(7 - 5) - 3
- Toán tử gán ngược lại ưu tiên từ phải qua trái
a = b = c
// Tương đương với biểu thức
a = (b = c)
Nếu không có quy tắc tốt về sự ưu tiên và sự liên kết tốt, việc phân tích cú pháp sẽ gặp những trường hợp khó hiểu phân tích thành nhiều cây cú pháp khác nhau từ một chuỗi token. ViL sử dụng quy tắc về ưu tiên và liên kết giống với C như sau:
| Tên | Toán tử | Liên kết |
|---|---|---|
| Tính bằng nhau (Equality) | == != |
Trái qua phải |
| Tính so sánh (Comparison) | > >= < <= |
Trái qua phải |
| Phép cộng trừ (Term) | + - |
Trái qua phải |
| Phép nhân chia (Factor) | * / |
Trái qua phải |
| Phép đảo (Unary) | ! - |
Phải qua trái |
Với bộ quy tắc hiện tại expression đại diện cho cả bốn loại biểu thức và chưa có sự ưu tiên. Quy tắc đó dễ dàng chấp nhận bất kì biểu thức nào không kể đó là biểu thức T hay NT.
Để sửa điều này ta sắp xếp từng quy tắc cho mỗi mức độ ưu tiên từ ít ưu tiên nhất đến mức độ ưu tiên mạnh nhất primary - kiểu số và chuỗi được built-in trong ViL và biểu thức nhóm grouping:
expression => ... ;
equality => ... ;
comparison => ... ;
term => ... ;
factor => ... ;
unary => ... ;
primary => ... ;
Mỗi quy tắc này chỉ hoạt động với độ ưu tiên cao hơn nó ví dụ quy tắc cộng trừ term hợp lệ với chuõi 5 + 6 - 7 hoặc 5 + 6 * 7 vì nó có độ ưu tiên thấp hơn bao quát factor.
Ok chúng ta hãy điền vào bảng quy tắc trống hiện tại. đầu tiên với quy tắc ít ưu tiên nhất equality.
expression => equality ;
Bạn có thẻ bỏ quy tắc
expressionvà chỉ sử dụngequalitytuy nhiên nó là một cái tên chung cho mức độ ưu tiên thấp nhất. Với các chương sau chúng ta sẽ thêm các quy tắc với mức độ ưu tiên thấp hơnequalityđiều này sẽ thay đổi quy tắc nhóm ởprimarynếu sử dụng trực tiếpequalitynên sử dụngexpressionnhư một cái tên đại diện cho tất cả biểu thức.
Bây giờ bắt đầu từ cuối bảng quy tắc, chúng ta sẽ phân tích độ ưu tiên từ cao nhất đến thấp nhất.
Quy tắc primary đương nhiên sẽ là các kiểu built-in của ViL: số, chuỗi và logic ngoài ra còn là nhóm biểu thức.
primary => số | chuỗi | "đúng" | "sai" | "(" expression ")" ;
unary chứa toán tử một ngôi ! và - ở phía trước.
unary => ( "!" | "-" ) unary ;
Với quy tắc này biểu thức ngớ ngẩn !-!true hoàn toàn hợp lệ với một quy tắc đệ quy. Nhưng với quy tắc như vậy sẽ không bao giờ có điểm dừng vì unary cũng chính là đệ quy của nó. Hãy sửa lại một chút cho nó một điểm dừng khi xét hết các toán tử một ngôi, quy tắc với độ ưu tiên cao hơn primary.
unary => ( "!" | "-" ) unary
| primary ;
Tương tự với phép nhân và chia. Đây là quy tắc factor tương tự chúng ta suy ra:
factor => factor ( "/" | "*" ) unary
| unary ;
Quy tắc này hoàn toàn ổn, nhưng để biểu diễn một cách tường minh hơn về sự liên kết từ trái qua phải của biểu thức factor mà bảng quy tắc liên kết bên trên ta sẽ đổi phép đệ quy factor sang một kiểu biểu diễn như sau:
factor => unary ( ( "/" | "*" ) unary )*
Kí tự
*để thể hiện quy tắc trong ngoặc sẽ có thể lặp lại không lần hoặc nhiều lần
- factor => unary là hợp lệ
- factor => unary "*" unary "/" unary cũng là một biểu thức hợp lệ
Với một chút sự thay đổi trong cú pháp ta đã thể hiện được sự ưu tiên qua cách biểu diễn quy tắc. Tương tự với các quy tắc tiếp theo chúng ta sẽ có bộ quy tắc mới:
expression => equality ;
equality => comparison ( ( "==" | "!=" ) comparison )* ;
comparison => term ( ( ">" | ">=" | "<" | "<=" ) term )* ;
term => factor ( ( "+" | "-" ) factor )* ;
factor => unary ( ( "/" | "*" ) unary )* ;
unary => ( "!" | "-" ) unary
| primary ;
primary => số | chuỗi | "đúng" | "sai" | "(" expression ")" ;
Phân tích cú pháp theo chiều từ trên xuống dưới với đệ quy
Có rất nhiều kĩ thuật phân tích cú pháp mà mình cũng không thực sự biết cách hoạt động của nó như nào như một bộ kĩ thuật phân tích với cách viết tắt LL(k), LR(1), LALR—và hàng loạt kĩ thuật như parser combinators, Earley parsers, the shunting yard algorithm, ... . Trong khuôn khổ series và với kiến thức hạn hẹp của mình, chúng ta sẽ sử dụng kĩ thuật truy xuất đệ quy (recursive descent).
Truy xuất đệ quy là cách đơn giản nhất để thực hiện trình phân tích cú pháp. Tuy nhiên, đơn giản mà không hề yếu nó nhanh, mạnh mẽ và có thể hỗ trợ xử lý lỗi phức tạp. Thực tế, GCC (Trình biên dịch C/C++), V8 (máy ảo JavaScript trong Chrome), Roslyn (trình biên dịch C # được viết bằng C #) và rất nhiều ngôn ngữ rất mạnh khác nữa cũng sử dụng. Khẳng định truy xuất đệ quy là một kĩ thuật tốt.
Truy xuất đệ quy đúng như tên gọi của nó, sẽ truy xuất từ biểu thức ở ngoài cùng (ở đây chính là expression) sau đó tiếp tục phân tích đến khi chạm đến ngưỡng không thể phân tích tiếp. Bộ quy tắc mới của chúng ta khi áp dụng vào code sẽ tương đương như sau:
| Kí hiệu quy tắc | Mã đại diện |
|---|---|
| T (Terminal) | Token từ bước Scanner |
| NT (Non-terminal) | Gọi hàm xử lí tương ứng với quy tắc |
| |
Câu lệnh if hoặc switch |
* hoặc + |
Vòng lặp while hoặc for |
? |
Câu lệnh if |
Lớp Parser
Hãy tạo một file mới tên là parser.dart trong thư mục lib của chúng ta:
Source: lib/parser.dart
import 'package:vil/token.dart';
class Parser {
Parser(this._tokens);
final List<Token> _tokens;
int _current = 0;
}
Giống như Scanner, Parser nhận vào một đầu vào "thô" là chuỗi các Token của Scanner trích xuất được và biến _current lưu vị trí đang xét hiện tại.
Với quy tắc đầu tiên:
expression => equality ;
expression và equality dựa theo bảng chuyển đổi chúng là NT nên ta sẽ chuyển quy tắc này thành hai hàm với tên gọi của nó
Source: lib/parser.dart sau biến _current và import lớp Expression
import 'package:vil/grammar/expression.dart';
...
class Parser {
...
Expression _expression() {
return _equality();
}
}
Trước khi đến với các quy tắc tiếp theo chúng ta cần một bộ "đồ chơi" giống với Scanner phục vụ cho việc truy xuất Token trong mảng và kiểm tra Token hợp lệ.
Source: lib/parser.dart bên dưới biến _current
/// Kiểm tra đã đến cuối chuỗi Token chưa
bool get _isAtEnd => _peek().type == TokenType.eof;
/// Truy xuất phần tử hiện tại
Token _peek() {
return _tokens[_current];
}
/// Truy xuất phần tử hiện tại và tăng [_current] thêm một
Token _skip() {
final token = _peek();
_current++;
return token;
}
/// Truy xuất phần tử phía trước
Token _previous() {
return _tokens[_current - 1];
}
/// Kiểm tra tính Token hiện tại có phải là [type] không
bool _check(TokenType type) {
if (_isAtEnd != false && _peek().type == type) {
return true;
}
return false;
}
// Kiểm tra tính Token hiện tại có phải là một trong số TokenType truyền vào hay không
bool _match(List<TokenType> types) {
for (final type in types) {
if (_check(type)) {
_skip();
return true;
}
}
return false;
}
Ok đã tạm đủ đồ chơi, đến với quy tắc tiếp theo equality:
equality => comparison ( ( "==" | "!=" ) comparison )* ;
Trong dart sẽ được biểu diễn:
Expression _equality() {
final expression = _comparison();
while (_match([TokenType.equalEqual, TokenType.bangEqual])) {
final operator = _previous();
final right = _comparison();
expression = Binary(expression, operator, right);
}
return expression;
}
( "==" | "!=" ) được xử lí qua hàm _match bằng cách kiểm tra token hiện tại có là token "==" hay "!=". Còn * được chuyển thành vòng while theo bảng chuyển đổi. Mọi thứ còn lại đơn giản chỉ là tiếp tục lắp ráp các quy tắc khác.
Tương tự với comparison, term và factor ta sẽ biểu diễn tương tự trong Dart:
comparison
Expression _comparison() {
var expression = _term();
while (_match([
TokenType.greater,
TokenType.greaterEqual,
TokenType.less,
TokenType.lessEqual,
])) {
final operator = _previous();
final right = _term();
expression = Binary(expression, operator, right);
}
return expression;
}
term
Expression _term() {
var expression = _factor();
while (_match([TokenType.plus, TokenType.minus])) {
final operator = _previous();
final right = _factor();
expression = Binary(expression, operator, right);
}
return expression;
}
factor
Expression _factor() {
var expression = _unary();
while (_match([TokenType.star, TokenType.slash])) {
final operator = _previous();
final right = _unary();
expression = Binary(expression, operator, right);
}
return expression;
}
Đến biểu thức unary lại hơi khác một chút, nó là biểu thức duy nhất hiện tại có tinh liên kết từ phải qua trái.
Expression _unary() {
if (_match([TokenType.bang, TokenType.minus])) {
final operator = _previous();
final right = _unary();
return Unary(operator, right);
}
return _primary();
}
Vậy là chúng ta đã đến với tầng ưu tiên cao nhất primary
primary => số | chuỗi | "đúng" | "sai" | "(" expression ")" ;
Hầu hết các quy tắc đều có dạng là T nên việc triển khai chỉ là đưa Token hiện tại vào biểu thức tương ứng.
Expression _primary() {
if (_match([TokenType.kSo, TokenType.kChuoi])) {
return Literal(_previous().literal);
}
if (_match([TokenType.kDung])) {
return Literal(true);
}
if (_match([TokenType.kSai])) {
return Literal(false);
}
if (_match([TokenType.leftParen])) {
final expression = _expression();
_consume(TokenType.rightParen, 'Thiếu ")" sau biểu thức.');
return Grouping(expression);
}
return _error('Loại Token chưa có trong bảng quy tắc.');
}
Xử lí lỗi cú pháp
Một trình phân tích cú pháp thực sự có hai nhiệm vụ:
- Thứ nhất: Từ một chuỗi Token hợp lệ, tạo một cây cú pháp tương ứng.
- Thứ hai: Từ một chuỗi Token hợp lệ, hãy phát hiện bất kỳ lỗi nào và cho lập trình viên biết về những sai lầm của họ.
Đừng đánh giá thấp nhiệm vụ thứ hai, trong tất cả các IDE hiện đại Parser luôn luôn chạy ngầm phục vụ cho việc highlight code, auto-complete. Trạng thái code của chúng ta hầu như sẽ ở dạng lỗi cú pháp trước khi đoạn code được hoàn thành.
Do vậy trình phân tích cú pháp cần đưa ra hướng dẫn để đưa mọi thứ về đúng quỹ đạo, ViL sẽ đưa ra lỗi giúp lập trình viên sửa lại lỗi.
Có một số yêu cầu khó khăn khi trình phân tích cú pháp gặp lỗi cú pháp. Trình phân tích cú pháp phải:
- Phát hiện và báo cáo lỗi.
- Tránh crash chương trình.
Đó là yêu cầu cơ bản của một trình báo lỗi, nhưng một trình phân tích cú pháp tốt nên:
- Nhanh. Máy tính nhanh hơn hàng nghìn lần so kể từ khi công nghệ phân tích cú pháp lần đầu tiên được phát minh. Những ngày cần tối ưu hóa trình phân tích cú pháp của bạn để nó có thể truy cập toàn bộ mã nguồn trong những vài phút. Nhưng kỳ vọng của các lập trình viên đã tăng lên nhanh chóng, nếu không muốn nói là nhanh hơn. Họ muốn file code của họ được phân tích lại cú pháp trong mili giây sau mỗi lần gõ.
- Báo cáo nhiều lỗi nhất trong một lần chạy. Việc sửa lỗi đầu tiên rất dễ thực hiện nhưng sẽ gây khó chịu cho lập trình viên nếu mỗi lần họ sửa lỗi trước mà tiếp theo đó lại một lỗi tiếp theo lại xuất hiện. Họ muốn xem toàn bộ lỗi có thể.
- Giảm thiểu báo cáo lỗi hệ quả. Bạn thiếu một dấu "}" và ngay lập tức tất cả các scope phía sau của bạn bị lỗi hệ quả, ViL cần tránh việc đó vì nó gây rối cho người sử dụng.
Hai yêu cầu cuối khá mâu thuẫn. Chúng ta muốn báo cáo càng nhiều lỗi càng tốt, nhưng chúng ta không lại muốn báo cáo những lỗi chỉ đơn thuần là tác dụng phụ của một lỗi trước đó.
Panic mode
Mỗi khi gặp lỗi trong lúc phân tích cú pháp, chương trình sẽ tiến vào trạng thái panic mode dừng việc phân tích và trả ra lỗi hiện tại. Chế độ được kích hoạt ngay lúc trình phân tích tìm ra lỗi.
Trước khi nó có thể quay lại phân tích cú pháp, nó cần phải có được trạng thái của nó và chuỗi token sắp tới được căn chỉnh sao cho token tiếp theo khớp với quy tắc đang được phân tích cú pháp. Quá trình này được gọi là đồng bộ hóa (synchronization).
Việc dừng lại không tiếp tục phân tích, giúp chúng ta trách lỗi hệ quả tuy nhiên sẽ phải đánh đổi các lỗi cú pháp phía sau sẽ bị bỏ qua.
Triển khai panic mode
Ở mục trước chúng ta đang triển khai phân tích biểu thức nhóm grouping. Sau khi phân tích biểu thức trong ngoặc ta cần đảm bảo nhóm đó được gói lại bằng việc kiểm tra token tiếp theo có phải là ) bằng hàm _consume(), những lỗi như này thường gây các lỗi hệ quả nên khi gặp ta đưa hệ thống vào panic mode và trả lại lỗi phân tích:
Source: lib/parser.dart, bên dưới hàm _match
Token _consume(TokenType type, String message) {
if (_check(type)) return _skip();
throw _error(_peek(), message);
}
Lỗi phân tích cần hai thông tin chính: Token có vấn đề và nội dung lỗi.
Source: lib/parser.dart, bên dưới hàm _consume
ParserError _error(Token token, String message) {
Vil.parserError(token, message);
return ParserError();
}
Source: lib/parser.dart, sau lớp Parser
class ParserError extends Error {}
Việc đầu tiên khi phát hiện lỗi là in nó ra màn hình, ta làm điều đó thông qua hàm parserError.
Source: lib/vil.dart, sau hàm error
static void parserError(Token token, String message) {
if (token.type == TokenType.eof) {
error(
errorIn: 'PARSER',
line: token.line,
col: token.col,
message: message,
errorAt: ' ở cuối file',
);
} else {
error(
errorIn: 'PARSER',
line: token.line,
col: token.col,
message: message,
errorAt: ' tại "${token.lexeme}"',
);
}
}
Kết thúc hàm _primary throw lỗi phân tích vì quy tắc chưa được triển khai.
Expression _primary() {
if (_match([TokenType.kSo, TokenType.kChuoi])) {
return Literal(_previous().literal);
}
if (_match([TokenType.kDung])) {
return Literal(true);
}
if (_match([TokenType.kSai])) {
return Literal(false);
}
if (_match([TokenType.leftParen])) {
final expression = _expression();
_consume(TokenType.rightParen, 'Thiếu ")" sau biểu thức.');
return Grouping(expression);
}
throw _error(_peek(), 'Token chưa có trong bảng quy tắc.');
}
Chúng ta còn thiếu một phương thức public gói lại bộ quy tắc và trả về biểu thức cuối cùng phân tích được.
Expression? parse() {
try {
return _expression();
} on ParserError catch (_) {
return null;
}
}
Chúng ta sẽ quay lại phương thức này sau khi chúng ta thêm các câu lệnh (statements) vào ngôn ngữ. Hiện tại, nó phân tích cú pháp một biểu thức duy nhất và trả về nó. Lỗi phân tích chỉ nên ảnh hưởng trong chính trình phân tích thôi nên ta bắt lỗi ngay tại hàm parse, nó sẽ không ảnh hương đến phần còn lại của trình thông dịch.
Để kiểm tra xem hoạt động của Parser mà chúng ta vừa tạo, mình sẽ sử dụng AstPrinter ở bài trước để hiển thị thành quả của chúng ta.
Source: lib/vil.dart sửa lại hàm run
static void run(String source) {
Scanner scanning = Scanner(source);
List<Token> tokens = scanning.scan();
Parser parser = Parser(tokens);
Expression? expression = parser.parse();
if (expression != null) {
print(AstPrinter().print(expression));
}
}
Lời kết
Xin chúc mừng, bạn đã hoàn thành thử thách! Đó thực sự là tất cả những gì cần có của một trình phân tích cú pháp tự viết.Chúng ta sẽ mở rộng bộ quy tắc trong các chương sau với phép gán (assignment), câu lệnh (statements) và các nội dung khác, nhưng không điều gì trong số đó phức tạp hơn các toán tử nhị phân (binary) mà chúng ta đã làm bên trên.
Hãy thử ngay trình thông dịch chúng ta vừa làm, xem cách chúng xử lí độ ưu tiên và tính liên kết một cách chính xác, không tệ với gần 200 dòng code.
Mã nguồn
Bạn có thể theo dõi mã nguồn từng bài viết tại đây. Đừng ngại để lại cho mình một sao nhé 😍



