Bài tiếp theo này có hơi đụng đến toán một chút, vì mình thích phân tích yếu tố này khoa học một xíu để mong hiểu được bản chất của âm thanh và âm nhạc mà ta thường bỏ qua. Phần 1-Rhythm của bài viết:

Pitch (cao độ):

    Cao độ là độ cao thấp của mỗi một nốt nhạc, đặc trưng bởi tần số (đơn vị Hz) phát ra của nốt nhạc đó. Tần số càng thấp thì nốt nghe càng trầm, tần số càng cao thì nghe càng bổng. Trong khuôn nhạc, cao độ chính là sự khác biệt về vị trí theo chiều dọc (dòng kẻ khác nhau) của một nốt nhạc.

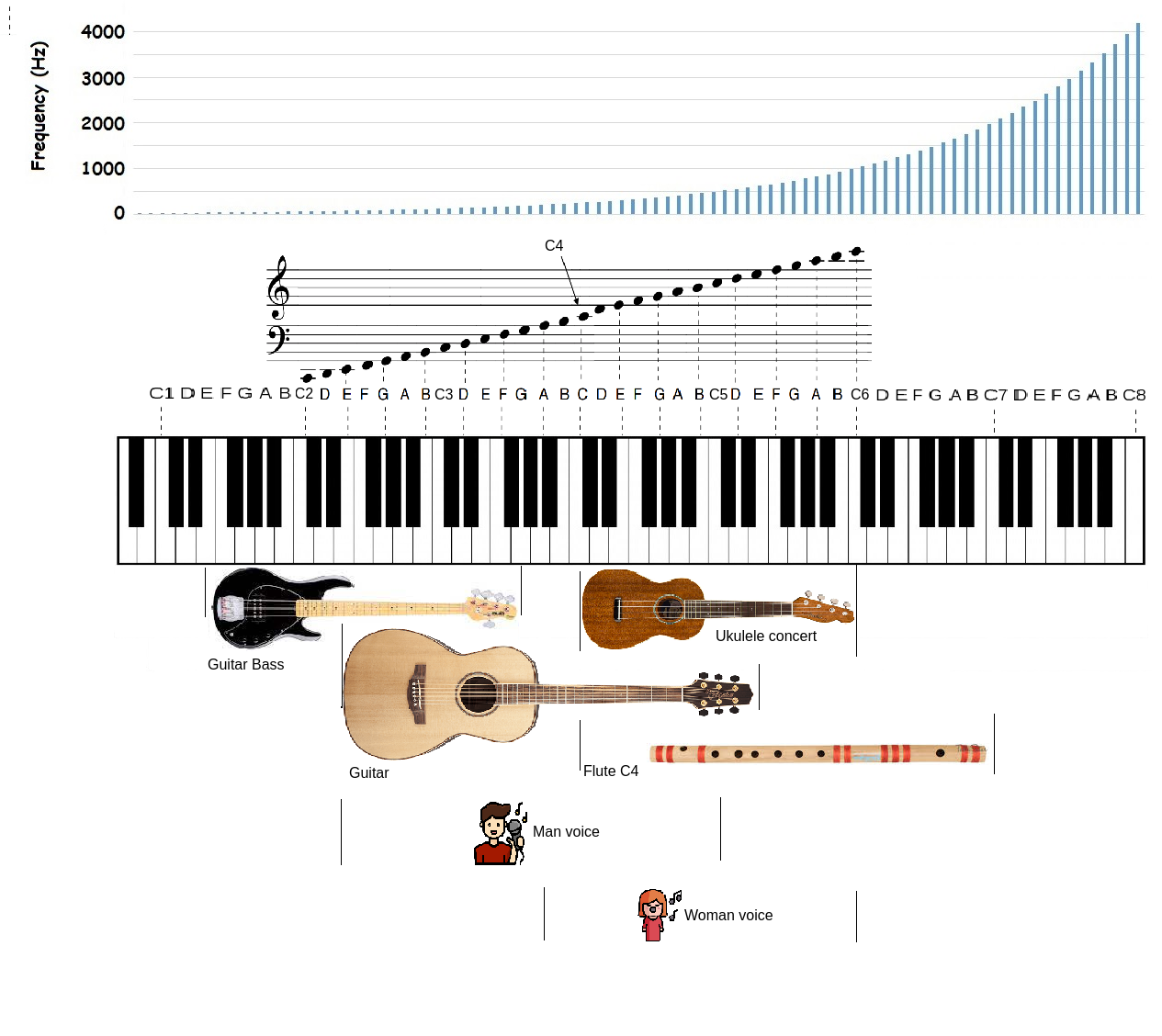
    Minh họa mối liên hệ giữa cao độ, tần số, ký hiệu trên khuôn nhạc và khoảng cao độ của một vài nhạc cụ.

    Khoảng tần số thường được sử dụng trải từ nốt C0 (~16.6Hz) đến C8 (~4100Hz), trong đó tần số nốt A4 ở vị trí thứ 69 giữa đàn piano đúng bằng 440Hz và được lấy làm chuẩn. Các nốt trước và sau đó được xác định theo công thức chuẩn MIDI. Theo công thức thì đại lượng p trong công thức là số thứ tự nốt nhạc, f là tần số Hz đầu vào:

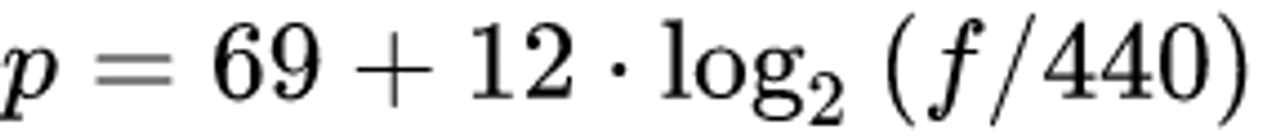
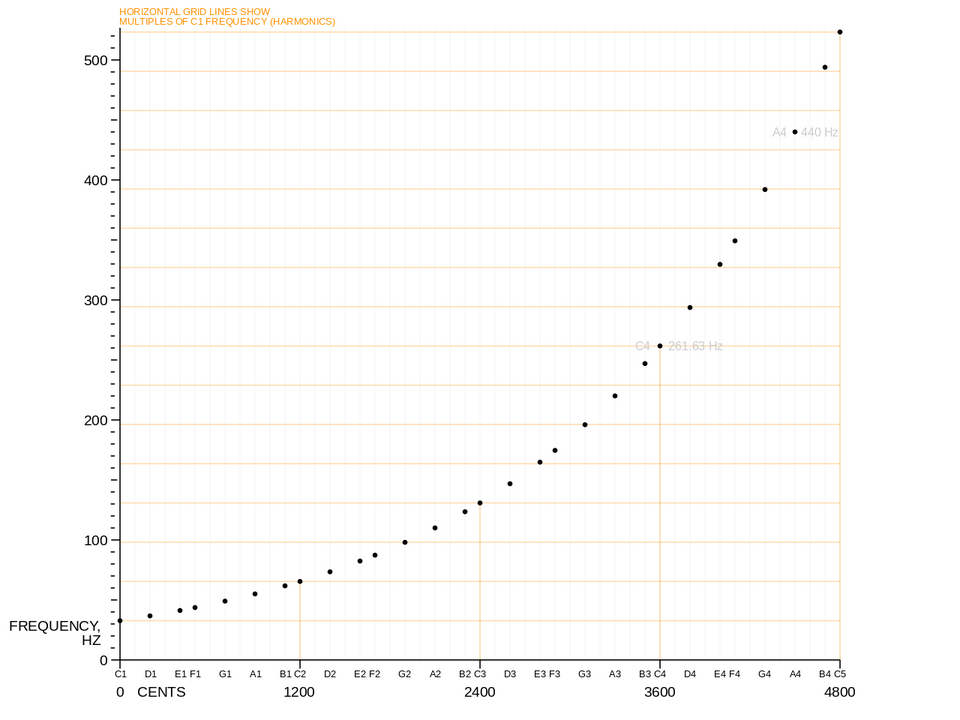
    Cá nhân mình thấy khá tò mò về con số 440Hz và quy tắc xác định theo hàm tuyến tính logaric. Chỉ nhớ mang máng là căn nguyên của sóng âm có dính đến log cơ số 2. Cơ mà nhìn biểu đồ phân chia khá đẹp, nên mình sẽ nghiên cứu và tổng hợp lại nguồn gốc của nó ở một bài viết khác.

    Mặc dù bản chất là khác nhau về tần số, người ta thường quy định khoảng cách giữa hai nốt bằng đơn vị cung (tone) và nửa cung (semitone). Theo đó, khoảng cách giữa 2 nốt liền nhau không kể đen trắng trên đàn piano là nửa cung, và quy thành 100 cent (như hình trên). Tiếp đến, nhiều nốt gần nhau lại được gom thành một tập hợp gọi là âm giai (scale) và phụ thuộc vào nốt bắt đầu (nốt gốc). Có nhiều cách gom như vậy để tạo thành một âm giai, trong đó phổ biến nhất là âm giai gồm 12 nửa cung gọi là Chromatic scale (1200 cent). Mỗi bộ 12 nửa cung gom thành một bậc hay một quãng, và có tính chất chu kỳ, nhưng độ lớn thì tăng dần.

    Trong 12 nốt của một âm giai này lại chọn ra một số lượng nhất định các nốt để làm nguyên liệu thô cơ bản nhất, kết hợp với rhythm để tạo thành một bản nhạc phức tạp. Các quãng khác cũng được chọn tương tự với cùng âm giai đó. 2 tập hợp được lựa chọn thường thấy nhất là âm giai trưởng (major) và thứ (minor):

• #Trưởng: cấu thành theo quy tắc khoảng cách giữa các nốt (tính theo nửa cung-100cent) là: 1-1-Nửa-1-1-1-Nửa. Ví dụ chọn 0 cent làm gốc, theo cách đặt tên nốt thì ta có C(0 cent)-D(200)-E(200)-F(100)-G(200)-A(200)-B(200)-C(100).
• #Thứ: Tương tự với Trưởng nhưng khác một chút: 1-nửa-1-1-nửa-1-1.

    Sở dĩ mình ghi ra cụ thể từng cent là để nhấn mạnh rằng còn có rất nhiều biến thể âm giai khác mặc dù không phổ biến, và không hẳn đo bằng chẵn 100cent. Trên thực tế chúng ta có thể chỉ sử dụng tuần tự từng nốt nhạc đơn rải đều cả bài nhạc, hoặc kết hợp nhiều nốt nhạc lại theo nhiều cách khác nhau. Trong đó cơ bản và chuẩn chỉnh nhất chủ yếu là 2 cách kết hợp theo chiều ngang (tạo thành melody) và theo chiều dọc (tạo thành chord):

Chord (hợp âm):

    Hợp âm Là sự kết hợp giữa 3 hay nhiều nốt được phát ra cùng lúc, trong đó nốt đầu tiên làm gốc. Các hợp âm cơ bản nhất sẽ gồm 3 nốt, được chọn dựa vào. Nguyên tắc cấu tạo của hợp âm cơ bản bao gồm nốt gốc + nốt thứ 3 + nốt thứ 5. Ví dụ Hợp âm C bao gồm 3 nốt C(1)-E(3)-G(5), trưởng hay thứ thì tùy thuộc vào loại âm giai mà ta chọn.

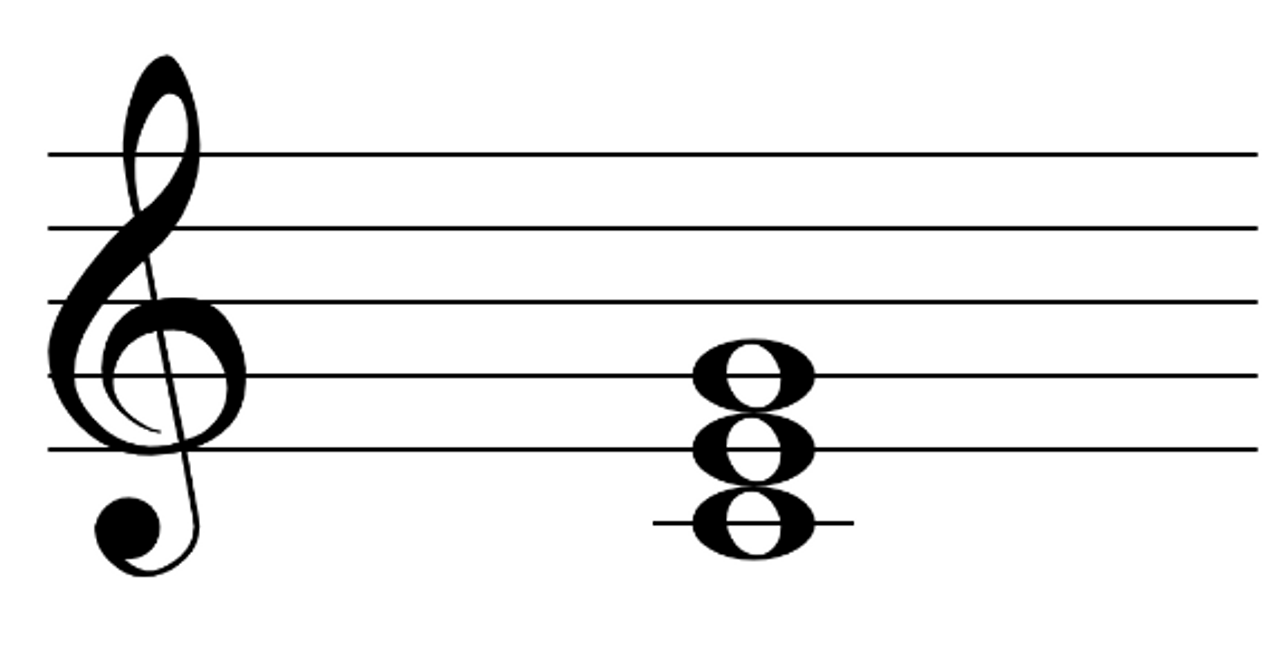
    Từ cái gốc cơ bản này mà các nhạc sĩ đã sáng tạo, tổng hợp và suy ra vô vàn các quy tắc và kỹ thuật kết hợp khác để hình thành nên nhiều loại hợp âm khác nhau, và có lẽ là không có giới hạn nào cho sự sáng tạo này.

Melody (làn điệu):

    Làn điệu là sự kết hợp của một chuỗi liên tiếp nhau của các nốt đơn, được phát ra tuần tự. Ranh giới giữa các làn điệu thường không thống nhất, tùy vào người chơi nhạc và người nghe. Có khi ta lấy ranh giới là vị trí các nhịp gõ, có khi tùy vào câu từ lúc hát, sự sáng tạo của người chơi, sự cảm thụ của người nghe...

Sử dụng phép biến đổi Fourier để xác định tần số của một sóng âm trong một audio:

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, ifft

sampleRate = 50
frequency = 2
audio_length = 5
amplitude = 1.0
t = np.linspace(0, audio_length, sampleRate * audio_length)
y = amplitude * np.sin(frequency * 2 * np.pi * t)


def sineWave():
    plt.plot(t, y)
    plt.title('Sine wave')
    plt.xlabel('Time')
    plt.grid(True, which='both')
    plt.axhline(y=0, color='k')
    plt.show()

sineWave()

    Input: Tự tạo một dải sóng sin có tần số bằng Qoutput:

def ff():
    ff_y = fft(y)
    true_ff_y = ff_y / (sampleRate * audio_length)
    plt.stem(t, true_ff_y, 'r', )
    plt.plot(t, true_ff_y)
    plt.title('FF y')
    plt.xlabel('Hz')
    plt.grid(True, which='both')
    plt.axhline(y=0, color='k')
    plt.show()
ff()

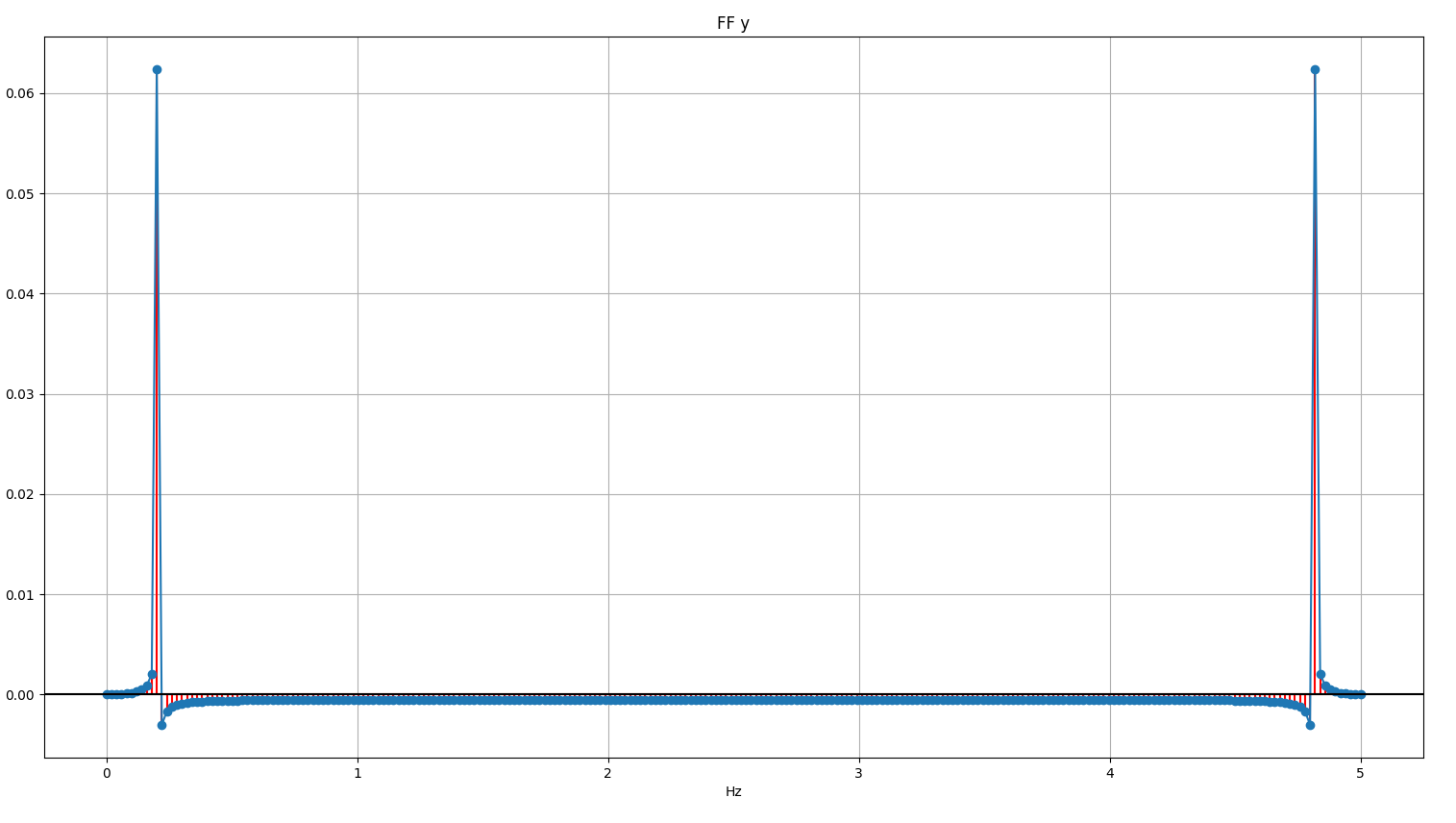
    Sau phép biến đổi Fourier (mình sẽ trình bày trong bài viết khác), ta trích xuất được dấu hiệu của tần số trong dải sóng âm đầu vào. Vị trí peek giá trị aplitude lên cao chính là giá trị tần số của sóng âm nguồn.

Kết:

    Trên đây là một số diễn giải trong hiểu biết của mình về cao độ trong âm nhạc. Cảm ơn bạn đã đọc bài viết. Bài tiếp theo mình sẽ viết về các thành tố khác trong âm nhạc là cường độ và âm sắc.

Tài liệu:

• https://en.wikipedia.org/wiki/Pitch_(music)
• The Basic Elements of Music - Catherine Schmidt-Jones http://textbookequity.org/category/music/