Lấy cảm hứng từ bài viết [Deep Learning] Graph Neural Network - A literature review and applications của tác giả @PhanHoang, nhân dịp đầu xuân năm mới mình dự định bắt đầu một chuỗi bài viết về chủ đề Grap Convolution Networks (GCN). Khởi đầu chuỗi bài viết này, chúng ta sẽ tìm hiểu về mô hình GCN qua bài nghiên cứu SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

    Dưới đây là một số thuật ngữ hoặc kí hiệu toán học mà mình sử dụng trong chuỗi bài này:

1. V: tập hợp các đỉnh của đồ thil
2. E: tập hợp các cạnh của đồ thị
3. D: ma trận đường chéo chứa thông tin bậc của mỗi đỉnh
4. A: ma trận vuông nhị phân (0 hoặc 1) chứa thông tin một nút có những hàng xóm hay nút kề nào
5. G: đồ thị được cấu thành.
6. N: số node của đồ thị
7. $X_{k} với k \in {1, ..., n}$
8. I: ma trận identity với các phần tử trên đường chéo bằng 1 còn khác sẽ bằng 0

1. Fast Approximate Convolution on Graphs.

    Graph Convolution Network lấy động lực phát triển từ Spectral Graph Convolution. Do đó trước khi đi vào phần chính, chúng ta cùng nhắc lại một chút kiến thức về Spectral Convolution Networks và Laplacian matrix.

1.1. Laplacian matrix

    Laplacian matrix là ma trận biểu diễn đồ thị được sử dụng rộng rãi trong nhiều ứng dụng của Machine Learning.

    Một số dạng biểu diễn đồ thị bằng Laplacian:

    Đồ thị vô hướng đơn giản với N đỉnh:

    $$L_{n \times n} = D - A$$

    Đồ thị có hướng đơn giản:

    Từng phần tử L nhận giá trị như sau:

    $$L_{i, j}:=\left\{\begin{array}{ll} \operatorname{deg}\left(v_{i}\right) & \text { nếu } i=j \\ -1 & \text { nếu } i \neq j \text { and } v_{i} \text { là đỉnh kề với } v_{j} \\ 0 & \text { khác } \end{array}\right.$$

    Hay Symmetric normalized Laplacian được sử dụng nhiều trong Machine Learning:

    $$L^{\text {sym }}:=D^{-\frac{1}{2}} L D^{-\frac{1}{2}}=I-D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$$

1.2. Spectral Graph Convolutions

    Ta thường nghe từ Spectral trong lĩnh vực xử lý tín hiệu. Trong lĩnh vực xử lý tín hiệu, chúng ta thường biển đổi tín hiệu sang dải tần số bằng có sử dụng biến đổi Fourier rời rạc. Hay nói một cách đơn giản hơn là nhân tín hiệu với một ma trận đặc biệt. Tuy nhiên công thức này dựa trên dữ liệu đầu vào là dạng lưới chứ không phải dạng graph. Do đó công thức spectral convolutions với dữ liệu đồ thị được biểu diễn như sau:

    $$g_{\theta}(L) \star x = Ug_{\theta}(\Lambda)U^{T}x = g_{\theta}'(\Lambda)x$$

    trong đó:

• $\theta$ là hệ số của spetracl filter
• U là ma trận vector riêng (eigenvector) của L
• $\Lambda$ là ma trận giá trị riêng (eigenvalues)
• $U^{T}x$ là giá trị sau biến đổi Fourier của x

    Tuy nhiên việc chi phí tính toán nhân ma trận vector riêng và tính eigendecomposition của L là quá lớn khi tăng kích thước của đồ thị. Để giải quyết vấn đề này, $g_{\theta}'(\Lambda)$ được biểu diễn dưới dạng đa thức Chebyshev như sau:

    $$g_{\theta}'(\Lambda) \approx \sum_{k=0}^{K}\theta_{k}T_{k}(\Lambda')$$

    trong đó $\Lambda = \frac{1}{2\lambda_{max}} \Lambda - I_{n}$. $\lambda_{max}$ là giá trị riêng lớn nhất của L và $\theta$ là vector hệ số Chebyshev.

    Vậy, ta có công thức mới tích chập một tín hiệu x với filter $g_{\theta}'$ có dạng như sau:

    $$g_{\theta}(L) \star x \approx \sum_{k=0}^{K }\theta_{k}T_{k}(\Lambda') x$$

1.3. Layer-Wise Linear Model

    Dựa trên công thức spectral graph convolution mới mà ta tìm được ở trên ta sẽ tìm cách biểu diễn chúng như một layer trong mô hình neuron network bình thường trong đó mỗi layer-wise linear đóng vai trò như một hidden layer.

    Một mô hình có thể xây dựng bằng nối nhiều lớp convolution lại với nhau, theo sau mỗi lớp conv là một point-wise non-linearity. Tuy nhiên để đơn giản cho bài viết ta giả sử số layer convolution K = 1, $\lambda_{max} = 2$. Như vậy công thức bên trên sẽ trở thành

    $$g_{\theta^{\prime}} \star x \approx \theta_{0}^{\prime} x+\theta_{1}^{\prime}\left(L-I_{N}\right) x=\theta_{0}^{\prime} x-\theta_{1}^{\prime} D^{-\frac{1}{2}} A D^{-\frac{1}{2}} x$$

    $\theta'_{0}, \theta'_{1}$ ở đây đóng vai trò như một tham số có thể huấn luyện. Để giới hạn số lượng tham số trong mô hình để giải quyết vấn đề overfiting, ta giả sử $\theta = \theta_{0}' = -\theta_{1}'$

    $$g_{\theta^{\prime}} \star x \approx \theta (I_{N} + D^{-1/2}AD^{-1/2})$$

    Các bạn có thể để ý các giá trị $I_{N} + D^{-1/2}AD^{-1/2}$ đều nằm trong khoảng [0, 2]. Giống như việc chúng ta cần phải thực hiện chuẩn hóa trong mạng neural network, ở GCN chúng ta cũng cần chuẩn hóa để tránh các hiện tượng gradient quá lớn hoặc quá nhỏ. Ở trong bài báo, tác giả có đề cập một phương pháp chuẩn hóa như sau:

    $$I_{N} + D^{-1/2}AD^{-1/2} = D'^{-1/2}A'D'^{-1/2}$$

    trong đó:

• $A' = A + I_{N}$
• $D'_{ii} = \sum_{j}A'_{ij}$

    Việc $I_{N}$ xuất hiện trong công thức chuẩn hóa có ý nghĩa hết sức quan trọng. Suy cho cùng, cái mà chúng ta muốn học ở đây chính là node embedding của mỗi node trên đồ thị. Do đó đặc trưng của từng node không những được tạo thành từ đặc trưng các node hàng xóm qua A mà còn từ chính bản thân node đó được biểu diễn qua identity matrix $I_{N}$.

    Kết lại, với một input feature là X, sau khi qua lớp layer-wise linear ta sẽ có output feature Z:

    $$Z = D'^{-1/2}A'D'^{-1/2}X\theta$$

2. Semi-supervised Node Classification.

    Layer-wise linear đóng vai trò như một hidden layer trong một mạng và như phần 1 mình đã trình bày công thức biểu diễn của lớp này khi nhận input feature X. Phần 2 này chỉ đơn giản là mô hình được tạo thành từ nhiều lớp Layer-wise linear thực hiện cho nhiệm vụ phân loại node thành các nhãn khác nhau tùy yêu cầu bài toán.

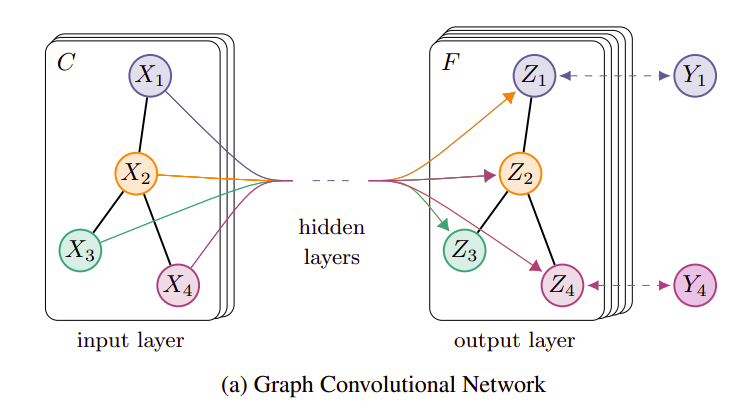
    Ví dụ như mô hình trên đây ta có số hidden layer bằng 2. Và tất nhiên hàm loss trong bài toán phân loại là cross-entropy:

    $$L = - \sum_{l \in Y_{L}}\sum_{f = 1}^{F}Y_{lf}lnZ_{lf}$$

    trong đó $Y_{L}$ là tập các node có nhãn.

    Mô hình GCN trong bài báo này đã đánh dấu một hướng đi mới trong việc giải quyết các bài toán có dữ liệu dạng đồ thị. Tuy nhiên cách huấn luyện kiểu full-batch gradient descent tức là đưa toàn bộ các node trong đồ thị cùng một lúc để tính toán dẫn đến các vấn đề không đủ bộ nhớ khi đồ thị trở nên lớn hơn, thời gian mỗi epoch lâu hơn hay gradient sẽ hội tụ chậm hơn so với các mô hình sau này.

3. Lời kết.

    Cảm ơn các bạn đã theo dõi bài viết của mình. Hy vọng bài viết mang lại nhiều góc nhìn cho các bạn về mô hình GCN trong bài nghiên cứu này. Các bạn hãy theo dõi các bài viết tiếp theo trong chuỗi bài viết về chủ đề này của mình nhé.

Tài liệu tham khảo

1. Understanding Graph Convolutional Networks for Node Classification
2. [Deep Learning] Graph Neural Network - A literature review and applications
3. SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS